Utilisateur:
Force visqueuse et gravitation
Storyboard 
Lorsqu'un objet se déplace dans un milieu visqueux sous l'influence d'une force constante comme la gravité, initialement la gravité accélère l'objet jusqu'à ce que sa vitesse augmente au point où la force visqueuse et la gravité s'équilibrent. À partir de ce moment, l'objet n'accélère plus et se déplace à une vitesse constante.
ID:(1965, 0)
Mécanismes
Iframe
Mécanismes
ID:(15539, 0)
Force visqueuse sur un corps
Top
La force subie par un corps se déplaçant à une vitesse de ($$) dans un milieu caractérisé par a constante de force visqueuse ($b$) est a force visqueuse ($F_v$), comme décrit par l'équation :
| $ F_v = b v $ |
Pour comprendre le rôle de a constante de force visqueuse ($b$), il est important de se rappeler que la viscosité est une mesure de la manière dont le moment, ou la vitesse des molécules, se diffuse. En d'autres termes, a constante de force visqueuse ($b$) représente la mesure selon laquelle le corps perd de l'énergie en la transférant au milieu et en accélérant les molécules, leur fournissant ainsi de l'énergie. Par conséquent, a constante de force visqueuse ($b$) est proportionnel à la viscosité.
ID:(15546, 0)
Forces sur une sphère tombant dans un milieu
Description
Lorsqu'une sphère est jetée dans un milieu visqueux, une force initiale ascendante, une force gravitationnelle ($F_g$), apparaît, entraînant progressivement l'enfoncement du corps. Pendant ce processus, la sphère gagne en vitesse, ce qui entraîne une force descendante, une force visqueuse ($F_v$), dépendante de la vitesse. Au fur et à mesure que la vitesse totale, a force à masse constante ($F$),
| $ F = F_g - F_v $ |
commence à diminuer jusqu'à devenir nulle. À partir de ce moment, le mouvement continue à une vitesse constante, car il n'y a pas de force pour l'accélérer.
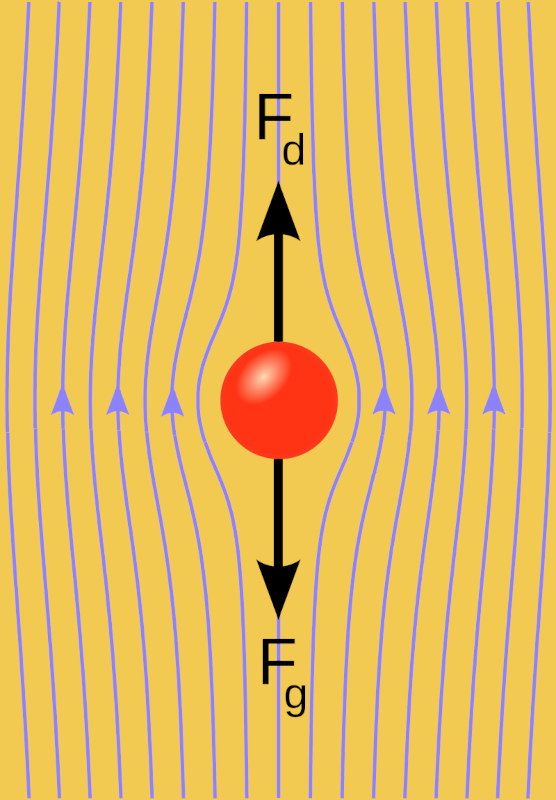
ID:(15544, 0)
Méthode d'Ostwald pour mesurer la viscosité
Description
La méthode de mesure de la viscosité d'Ostwald est basée sur le comportement d'un liquide s'écoulant à travers un tube de petit rayon (capillaire).
Le liquide est introduit, une aspiration est appliquée pour dépasser la marque supérieure, puis il est laissé s'écouler, mesurant le temps qu'il faut pour que le niveau passe de la marque supérieure à la marque inférieure.
L'expérience est d'abord réalisée avec un liquide pour lequel la viscosité et la densité sont connues (par exemple, de l'eau distillée), puis avec le liquide pour lequel la viscosité doit être déterminée. Si les conditions sont identiques, le liquide qui s'écoule dans les deux cas sera similaire, et ainsi, le temps sera proportionnel à la densité divisée par la viscosité. Ainsi, une équation de comparaison entre les deux viscosités peut être établie :
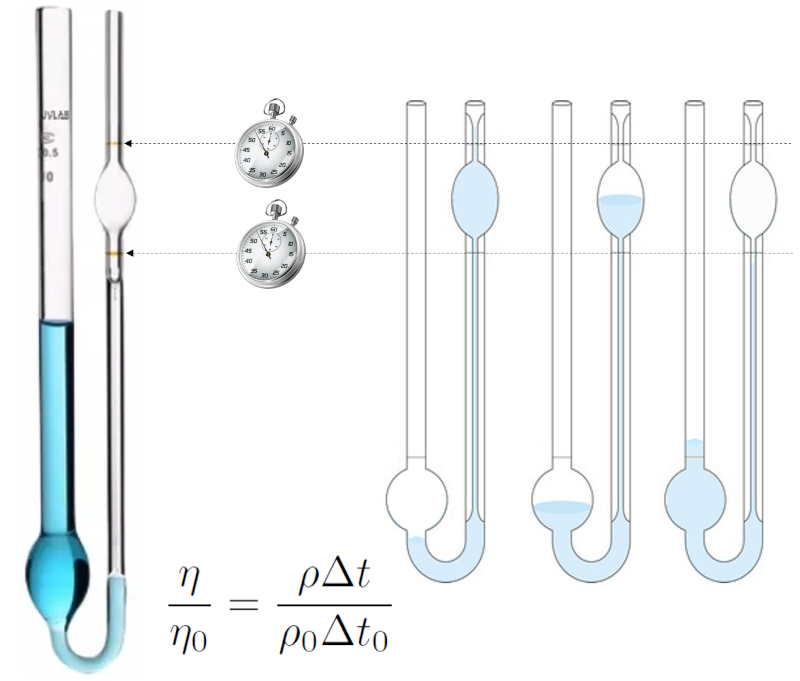
ID:(15545, 0)
Vitesse de chute en milieu visqueux
Top
Dans le cas d'un corps tombant dans un milieu visqueux, l'équation de mouvement est une équation de a vitesse ($v$) en fonction de le temps ($t$) avec a masse gravitationnelle ($m_g$), a masse d'inertie ($m_i$), a accélération gravitationnelle ($g$) et a constante de force visqueuse ($b$) :
| $ m_i \displaystyle\frac{dv}{dt} = m_g g - b v $ |
Cela est obtenu avec a temps de viscosité et masse d'inertie ($\tau_i$)
| $ \tau_i \equiv \displaystyle\frac{ m_i }{ b }$ |
et avec a temps de viscosité et masse gravitationnelle ($\tau_g$)
| $ \tau_g \equiv \displaystyle\frac{ m_g }{ b }$ |
En intégrant avec un temps initial nul et a vitesse initiale ($v_0$),
| $ v = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
qui est représentée ci-dessous :
Le graphique illustre comment la viscosité contraint le corps à descendre avec une vitesse asymptotique ($v_{\infty}$), ce qui équivaut à $g\tau_g$. Cela se produit en un temps de l'ordre de a temps de viscosité et masse d'inertie ($\tau_i$), que a vitesse ($v$) soit inférieur ou supérieur à A vitesse asymptotique ($v_{\infty}$).
ID:(15547, 0)
Chemin de chute en milieu visqueux
Top
Dans le cas d'un corps tombant dans un milieu visqueux, l'équation de mouvement est une équation de a position ($s$) en fonction de a accélération gravitationnelle ($g$), a temps de viscosité et masse d'inertie ($\tau_i$), a temps de viscosité et masse gravitationnelle ($\tau_g$), a vitesse initiale ($v_0$) et le temps ($t$) :
| $ \displaystyle\frac{ds}{dt} = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
À partir de cette équation, nous obtenons en intégrant avec un temps initial nul et une vitesse ($s_0$) :
| $ s = s_0 + g \tau_g t +( v_0 - g \tau_g ) \tau_i (1 - e^{- t / \tau_i })$ |
qui est représentée ci-dessous :
ID:(15550, 0)
Modèle
Top
Paramètres
Variables
Calculs
à 
, puis, sélectionnez la variable: 
à 
Calculs
Calculs
Variable 
Donnée Calculer 
Cible : Équation À utiliser 
Équations
$ \displaystyle\frac{ds}{dt} = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$
@DIFF( s , t )= g * tau_g + ( v_0 - g * tau_g )*exp(- t / tau_i )
$ F = F_g - F_v $
F = F_g - F_v
$ F = m_i a $
F = m_i * a
$ F_g = m_g g $
F_g = m_g * g
$ F_v = b v $
F_v = b * v
$ m_g = m_i $
m_g = m_i
$ m_i \displaystyle\frac{dv}{dt} = m_g g - b v $
m_i * @DIFF( v , t ) = m_g * g - b * v
$ m_i a = m_g g - b v $
m_i * a = m_g * g - b * v
$ s = s_0 + g \tau_g t +( v_0 - g \tau_g ) \tau_i (1 - e^{- t / \tau_i })$
s = s_0 + g * tau_g * t + ( v_0 - g * tau_g )* tau_i *(1-exp(- t / tau_i ))
$ \tau_g \equiv \displaystyle\frac{ m_g }{ b }$
tau_g = m_g / b
$ \tau_i \equiv \displaystyle\frac{ m_i }{ b }$
tau_i = m_i / b
$ v = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$
v = g * tau_g + ( v_0 - g * tau_g )*exp(- t / tau_i )
$ v_{\infty} \equiv g \tau_g $
v_i = g * tau_g
ID:(15541, 0)
Force totale du corps tombant dans un milieu visqueux
Équation
Dans le cas d'un corps tombant dans un milieu visqueux, la force totale, a force à masse constante ($F$), est égale à A force gravitationnelle ($F_g$) moins a force visqueuse ($F_v$), donc
| $ F = F_g - F_v $ |
ID:(15543, 0)
Cas de force masse constante
Équation
Dans le cas où A masse d'inertie ($m_i$) est égal à A masse initiale ($m_0$),
| $ m_g = m_i $ |
la dérivée de la quantité de mouvement sera égale à la masse multipliée par la dérivée de a vitesse ($v$). Comme la dérivée de la vitesse est a accélération instantanée ($a$), nous avons que a force à masse constante ($F$) est égal à
| $ F = m_i a $ |
Étant donné que le moment ($p$) est défini avec a masse d'inertie ($m_i$) et a vitesse ($v$),
| $ p = m_i v $ |
Si a masse d'inertie ($m_i$) est égal à A masse initiale ($m_0$), alors nous pouvons dériver la quantité de mouvement par rapport au temps et obtenir a force à masse constante ($F$) :
$F=\displaystyle\frac{d}{dt}p=m_i\displaystyle\frac{d}{dt}v=m_ia$
Par conséquent, nous en concluons que
| $ F = m_i a $ |
ID:(10975, 0)
Force visqueuse
Équation
La forme la plus simple de a force visqueuse ($F_v$) est celle qui est proportionnelle au a vitesse ($v$) du corps, représentée par :
| $ F_v = b v $ |
La constante de proportionnalité, également connue sous le nom de a constante de force visqueuse ($b$), dépend généralement de la forme de l'objet et de la viscosité du milieu à travers lequel il se déplace. Un exemple de ce type de force est celle exercée par un flux de fluide sur un corps sphérique, dont l'expression mathématique est connue sous le nom de loi de Stokes.
ID:(3243, 0)
Force gravitationnelle
Équation
A force gravitationnelle ($F_g$) est basé sur a masse gravitationnelle ($m_g$) de l'objet et sur une constante qui reflète l'intensité de la gravité à la surface de la planète. Cette dernière est identifiée par a accélération gravitationnelle ($g$), qui est égal à $9.8 m/s^2$.
Par conséquent, on en conclut que :
| $ F_g = m_g g $ |
ID:(3241, 0)
Égalité des masses inertielle et gravitationnelle
Équation
Les masses que Newton a utilisées dans ses principes sont liées à l'inertie des corps, ce qui conduit au concept de a masse d'inertie ($m_i$).
La loi de Newton, qui est liée à la force entre les corps en raison de leurs masses, est associée à la gravité et est donc connue sous le nom de a masse gravitationnelle ($m_g$).
Empiriquement, on a conclu que les deux masses sont équivalentes, et donc nous définissons
| $ m_g = m_i $ |
Einstein a été celui qui a remis en question cette égalité et, à partir de ce doute, a compris pourquoi les deux 'apparaissent' égales dans sa théorie de la gravité. Dans son argument, Einstein a expliqué que les masses déforment l'espace, et cette déformation de l'espace provoque un changement dans le comportement des corps. Ainsi, les masses s'avèrent être équivalentes. Le concept révolutionnaire de la courbure de l'espace implique même que la lumière, qui n'a pas de masse, est affectée par les corps célestes, ce qui contredit la théorie de la gravitation de Newton. Cela a été démontré expérimentalement en étudiant le comportement de la lumière lors d'une éclipse solaire. Dans cette situation, les faisceaux lumineux sont déviés en raison de la présence du soleil, permettant l'observation des étoiles qui se trouvent derrière lui.
ID:(12552, 0)
Équation de mouvement tombant dans un milieu visqueux
Équation
A force à masse constante ($F$) est égal à A force gravitationnelle ($F_g$) moins a force visqueuse ($F_v$), donc :
| $ F = F_g - F_v $ |
Cette relation permet d'établir l'équation de mouvement pour a accélération instantanée ($a$) avec une masse d'inertie ($m_i$) qui chute en raison de la gravité terrestre avec a accélération gravitationnelle ($g$), et avec une masse gravitationnelle ($m_g$), en a constante de force visqueuse ($b$), prendra la forme de :
| $ m_i a = m_g g - b v $ |
ID:(14495, 0)
Équation différentielle de la chute en milieu visqueux
Équation
A masse d'inertie ($m_i$) qui chute sous l'effet de la gravité terrestre avec une accélération gravitationnelle ($g$), et avec une masse gravitationnelle ($m_g$) dans un milieu visqueux avec une constante de force visqueuse ($b$), est présenté comme suit :
| $ m_i a = m_g g - b v $ |
Pour résoudre cette équation, il est nécessaire de la ramener à sa forme différentielle. Cela est réalisé en remplaçant a accélération instantanée ($a$) par la dérivée de a vitesse ($v$) en le temps ($t$) :
| $ m_i \displaystyle\frac{dv}{dt} = m_g g - b v $ |
ID:(14492, 0)
Temps de masse gravitationnelle et viscosité
Équation
Avec l'équation de mouvement d'un corps dans un milieu visqueux, nous avons la dérivée de a vitesse ($v$) à Le temps ($t$) avec a masse d'inertie ($m_i$), a masse gravitationnelle ($m_g$), a constante de force visqueuse ($b$) et a accélération gravitationnelle ($g$) :
| $ m_i \displaystyle\frac{dv}{dt} = m_g g - b v $ |
Cela définit a temps de viscosité et masse d'inertie ($\tau_i$) comme :
| $ \tau_g \equiv \displaystyle\frac{ m_g }{ b }$ |
ID:(15549, 0)
Temps de masse inertielle et viscosité
Équation
Avec l'équation de mouvement d'un corps dans un milieu visqueux, nous avons la dérivée de a vitesse ($v$) à Le temps ($t$) avec a constante de force visqueuse ($b$) et a accélération gravitationnelle ($g$) :
| $ m_i \displaystyle\frac{dv}{dt} = - b v $ |
Cela définit a temps de viscosité et masse d'inertie ($\tau_i$) comme :
| $ \tau_i \equiv \displaystyle\frac{ m_i }{ b }$ |
ID:(15548, 0)
Solution du mouvement tombant dans un milieu visqueux
Équation
L'équation du mouvement en a vitesse ($v$) à Le temps ($t$) avec a masse d'inertie ($m_i$), a masse gravitationnelle ($m_g$), a accélération gravitationnelle ($g$), et a constante de force visqueuse ($b$) est :
| $ m_i \displaystyle\frac{dv}{dt} = m_g g - b v $ |
En supposant que le temps initial soit nul, a vitesse initiale ($v_0$), a temps de viscosité et masse gravitationnelle ($\tau_g$) et a temps de viscosité et masse d'inertie ($\tau_i$), nous obtenons l'équation suivante :
| $ v = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
L'équation de mouvement à A vitesse ($v$) en le temps ($t$) avec a masse d'inertie ($m_i$), a masse gravitationnelle ($m_g$), a accélération gravitationnelle ($g$) et a constante de force visqueuse ($b$) :
| $ m_i \displaystyle\frac{dv}{dt} = m_g g - b v $ |
avec la définition de a temps de viscosité et masse d'inertie ($\tau_i$)
| $ \tau_i \equiv \displaystyle\frac{ m_i }{ b }$ |
et de a temps de viscosité et masse gravitationnelle ($\tau_g$)
| $ \tau_g \equiv \displaystyle\frac{ m_g }{ b }$ |
peut être reformulée comme suit :
$\displaystyle\frac{dv}{g\tau_g - v} = \displaystyle\frac{dt}{\tau_i}$
Si nous intégrons cette expression entre une vitesse initiale ($v_0$) et a vitesse ($v$), et du temps initial zéro jusqu'à Le temps ($t$), nous obtenons
$\ln(g\tau_g-v_0)-\ln(g\tau_g-v)=\displaystyle\frac{t}{\tau_i}$
En résolvant pour la vitesse, nous obtenons
| $ v = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
Cette équation illustre que a vitesse initiale ($v_0$) converge alors asymptotiquement vers la vitesse $g\tau_g$.
ID:(14493, 0)
Vitesse asymptotique
Équation
L'intégration de l'équation du mouvement donne a vitesse ($v$) en fonction de a accélération gravitationnelle ($g$), a temps de viscosité et masse d'inertie ($\tau_i$), a temps de viscosité et masse gravitationnelle ($\tau_g$), a vitesse initiale ($v_0$) et le temps ($t$) sous la forme :
| $ v = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
Pour le temps ($t$) beaucoup plus grand que a temps de viscosité et masse d'inertie ($\tau_i$), la limite a vitesse asymptotique ($v_{\infty}$) est obtenue :
| $ v_{\infty} \equiv g \tau_g $ |
ID:(14494, 0)
Équation différentielle de chute dans un milieu visqueux
Équation
L'intégration de l'équation du mouvement donne a vitesse ($v$) en fonction de a accélération gravitationnelle ($g$), a temps de viscosité et masse d'inertie ($\tau_i$), a temps de viscosité et masse gravitationnelle ($\tau_g$), a vitesse initiale ($v_0$) et le temps ($t$) sous la forme :
| $ v = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
dans sa forme différentielle,
| $ \displaystyle\frac{ds}{dt} = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
où A position ($s$) représente la distance parcourue.
ID:(14496, 0)
Chemin de chute dans un milieu visqueux
Équation
L'intégration de l'équation de mouvement produit a position ($s$) en fonction de a accélération gravitationnelle ($g$), a temps de viscosité et masse d'inertie ($\tau_i$), a temps de viscosité et masse gravitationnelle ($\tau_g$), a vitesse initiale ($v_0$) et le temps ($t$) comme suit :
| $ \displaystyle\frac{ds}{dt} = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
à partir d'un temps initial nul jusqu'à Le temps ($t$), et de a vitesse ($s_0$) jusqu'à A position ($s$), nous obtenons :
| $ s = s_0 + g \tau_g t +( v_0 - g \tau_g ) \tau_i (1 - e^{- t / \tau_i })$ |
ID:(14497, 0)