Usuario:
Fuerza viscosa y gravitación
Storyboard 
Cuando un cuerpo se desplaza en un medio viscoso bajo la influencia de una fuerza constante, como la gravedad, inicialmente la gravedad acelera el cuerpo hasta que su velocidad aumenta al punto en que la fuerza viscosa y la gravedad se equilibran. A partir de este punto, el cuerpo ya no experimenta aceleración y se desplaza a una velocidad constante.
ID:(1965, 0)
Mecanismos
Iframe
Mecanismos
ID:(15539, 0)
Fuerza viscosa sobre un cuerpo
Top
La fuerza experimentada por un cuerpo que se desplaza con una velocidad de ($$) en un medio, y que está caracterizado por la constante de fuerza viscosa ($b$), es la fuerza viscosa ($F_v$), como se describe por la ecuación:
| $ F_v = b v $ |
Para comprender el papel de la constante de fuerza viscosa ($b$), es importante recordar que la viscosidad es una medida de cómo se difunde el momento, es decir, la velocidad de las moléculas. En otras palabras, la constante de fuerza viscosa ($b$) es la medida en la que el cuerpo pierde energía al transferirla al medio y al acelerar las moléculas, entregándoles energía. Por lo tanto, la constante de fuerza viscosa ($b$) es proporcional a la viscosidad.
ID:(15546, 0)
Fuerzas sobre una esfera que cae en un medio
Descripción
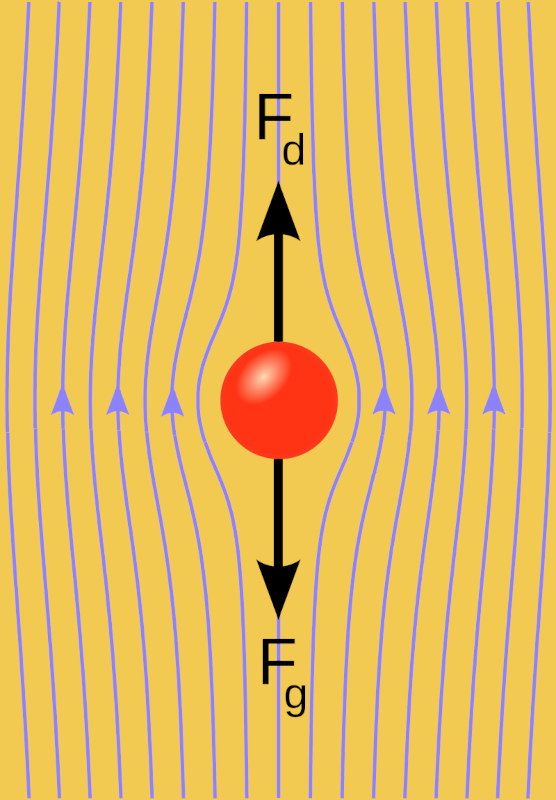
Cuando se arroja una esfera en un medio viscoso, aparece una fuerza ascendente inicial, una fuerza gravitacional ($F_g$), que comienza a hundir progresivamente el cuerpo. Durante este proceso, la esfera gana velocidad, dando lugar a una fuerza descendente, una fuerza viscosa ($F_v$), que depende de la velocidad. A medida que la velocidad total, la fuerza con masa constante ($F$),
| $ F = F_g - F_v $ |
comienza a reducirse hasta volverse nula. A partir de este momento, el movimiento continúa a una velocidad constante, ya que no hay fuerza que lo acelere.
ID:(15544, 0)
Método de Ostwald para medir viscosidad
Descripción
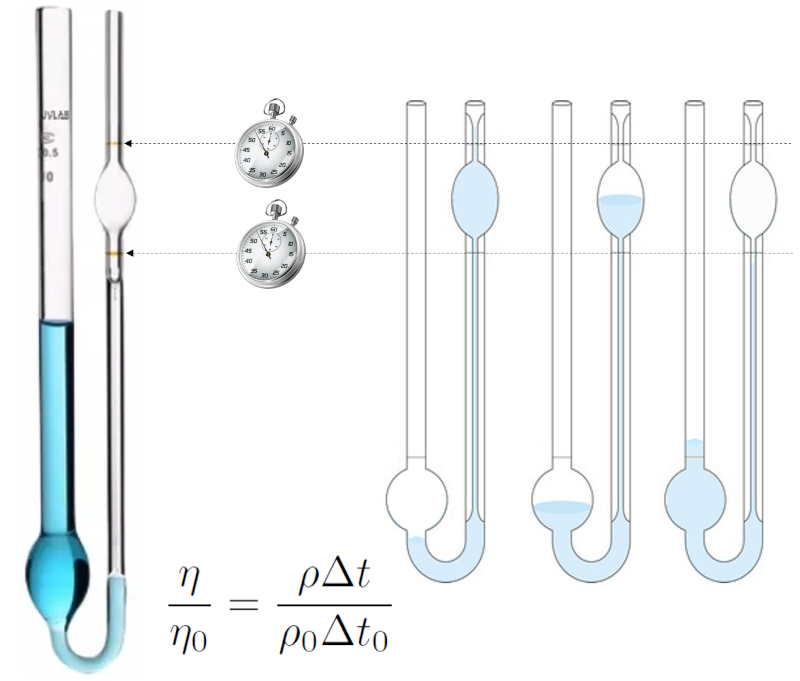
El método de medición de viscosidad de Ostwald se basa en el comportamiento de un líquido que fluye por un tubo de radio pequeño (capilar).
Se introduce el líquido, se succiona para que su nivel sobrepase la marca superior y luego se deja escurrir, midiendo el tiempo que el nivel tarda en pasar del nivel superior al inferior.
El experimento se realiza primero con un líquido para el cual se conoce la viscosidad y densidad (por ejemplo, agua destilada), y luego con el líquido para el cual se busca determinar la viscosidad. Si las condiciones son iguales, el líquido que fluya en ambos casos será similar, y con ello, el tiempo será proporcional a la densidad dividida por la viscosidad. Así, se puede establecer una ecuación de comparación entre ambas viscosidades:
ID:(15545, 0)
Velocidad de caída en medio viscoso
Top
En el caso de un cuerpo cayendo en un medio viscoso, la ecuación de movimiento es una ecuación de la velocidad ($v$) en función de el tiempo ($t$) con la masa gravitacional ($m_g$), la masa inercial ($m_i$), la aceleración gravitacional ($g$) y la constante de fuerza viscosa ($b$):
| $ m_i \displaystyle\frac{dv}{dt} = m_g g - b v $ |
Esto se obtiene con la tiempo de viscosidad y masa inercial ($\tau_i$)
| $ \tau_i \equiv \displaystyle\frac{ m_i }{ b }$ |
y con la tiempo de viscosidad y masa gravitacional ($\tau_g$)
| $ \tau_g \equiv \displaystyle\frac{ m_g }{ b }$ |
Integrando con tiempo inicial nulo y la velocidad inicial ($v_0$),
| $ v = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
que se representa a continuación:
El gráfico muestra cómo la viscosidad fuerza al cuerpo a descender con una velocidad asintótica ($v_{\infty}$), que es igual a $g\tau_g$. Esto ocurre en un tiempo del orden de la tiempo de viscosidad y masa inercial ($\tau_i$), tanto cuando la velocidad ($v$) es menor como mayor que la velocidad asintótica ($v_{\infty}$).
ID:(15547, 0)
Camino de caída en medio viscoso
Top
En el caso de un cuerpo cayendo en un medio viscoso, la ecuación de movimiento es una ecuación de la posición ($s$) en función de la aceleración gravitacional ($g$), la tiempo de viscosidad y masa inercial ($\tau_i$), la tiempo de viscosidad y masa gravitacional ($\tau_g$), la velocidad inicial ($v_0$) y el tiempo ($t$):
| $ \displaystyle\frac{ds}{dt} = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
A partir desta equação, obtém-se integrando com tempo inicial zero e una posición inicial ($s_0$):
| $ s = s_0 + g \tau_g t +( v_0 - g \tau_g ) \tau_i (1 - e^{- t / \tau_i })$ |
que se representa a continuación:
ID:(15550, 0)
Modelo
Top
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
$ \displaystyle\frac{ds}{dt} = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$
@DIFF( s , t )= g * tau_g + ( v_0 - g * tau_g )*exp(- t / tau_i )
$ F = F_g - F_v $
F = F_g - F_v
$ F = m_i a $
F = m_i * a
$ F_g = m_g g $
F_g = m_g * g
$ F_v = b v $
F_v = b * v
$ m_g = m_i $
m_g = m_i
$ m_i \displaystyle\frac{dv}{dt} = m_g g - b v $
m_i * @DIFF( v , t ) = m_g * g - b * v
$ m_i a = m_g g - b v $
m_i * a = m_g * g - b * v
$ s = s_0 + g \tau_g t +( v_0 - g \tau_g ) \tau_i (1 - e^{- t / \tau_i })$
s = s_0 + g * tau_g * t + ( v_0 - g * tau_g )* tau_i *(1-exp(- t / tau_i ))
$ \tau_g \equiv \displaystyle\frac{ m_g }{ b }$
tau_g = m_g / b
$ \tau_i \equiv \displaystyle\frac{ m_i }{ b }$
tau_i = m_i / b
$ v = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$
v = g * tau_g + ( v_0 - g * tau_g )*exp(- t / tau_i )
$ v_{\infty} \equiv g \tau_g $
v_i = g * tau_g
ID:(15541, 0)
Fuerza total de cuerpo que cae en medio viscoso
Ecuación
En el caso de un cuerpo que cae en un medio viscoso, la fuerza total, la fuerza con masa constante ($F$), es igual a la fuerza gravitacional ($F_g$) menos la fuerza viscosa ($F_v$), por lo tanto,
| $ F = F_g - F_v $ |
ID:(15543, 0)
Fuerza caso masa constante
Ecuación
En el caso en que la masa inercial ($m_i$) es igual a la masa inicial ($m_0$),
| $ m_g = m_i $ |
la derivada del momento será igual a la masa multiplicada por la derivada de la velocidad ($v$). Dado que la derivada de la velocidad es la aceleración instantanea ($a$), obtenemos que la fuerza con masa constante ($F$) es igual a
| $ F = m_i a $ |
Dado que el momento ($p$) se define con la masa inercial ($m_i$) y la velocidad ($v$),
| $ p = m_i v $ |
Si la masa inercial ($m_i$) es igual a la masa inicial ($m_0$), entonces podemos derivar el momento respecto al tiempo y obtener la fuerza con masa constante ($F$):
$F=\displaystyle\frac{d}{dt}p=m_i\displaystyle\frac{d}{dt}v=m_ia$
Por lo tanto, llegamos a la conclusión de que
| $ F = m_i a $ |
ID:(10975, 0)
Fuerza viscosa
Ecuación
La forma más simple de la fuerza viscosa ($F_v$) es aquella que es proporcional a la velocidad ($v$) del cuerpo, representada por:
| $ F_v = b v $ |
La constante de proporcionalidad, también conocida como la constante de fuerza viscosa ($b$), depende en general de la forma del objeto y de la viscosidad del medio en el que se desplaza. Un ejemplo de este tipo de fuerza es la que ejerce una corriente sobre un cuerpo esférico, cuya expresión matemática se conoce como la ley de Stokes.
ID:(3243, 0)
Fuerza gravitacional
Ecuación
La fuerza gravitacional ($F_g$) se basa en la masa gravitacional ($m_g$) del objeto y en una constante que refleja la intensidad de la gravedad en la superficie del planeta. Esta última es identificada por la aceleración gravitacional ($g$), que es igual a $9.8 m/s^2$.
En consecuencia, se concluye que:
| $ F_g = m_g g $ |
ID:(3241, 0)
Igualdad de masa inercial y gravitacional
Ecuación
Las masas que Newton utilizó en sus principios están relacionadas con la inercia de los cuerpos, lo que lleva al concepto de la masa inercial ($m_i$).
La ley de Newton que se vincula con la fuerza entre cuerpos debido a sus masas está relacionada con la gravedad, por lo que se conoce como la masa gravitacional ($m_g$).
De manera empírica, se ha concluido que ambas masas son equivalentes, y por lo tanto, definimos
| $ m_g = m_i $ |
Einstein fue quien cuestionó esta igualdad y, a partir de esa duda, comprendió por qué ambas 'aparecen' iguales en su teoría de la gravedad. En su argumento, Einstein explicó que las masas deforman el espacio, y esta deformación del espacio provoca un cambio en el comportamiento de los cuerpos. De esta manera, las masas resultan ser equivalentes. El concepto revolucionario de la curvatura del espacio implica que incluso la luz, que carece de masa, se ve afectada por los cuerpos celestes, lo que contradice la teoría de la gravitación de Newton. Esto se demostró experimentalmente al estudiar el comportamiento de la luz durante un eclipse solar. En esta situación, los haces de luz se desvían debido a la presencia del sol, lo que permite observar estrellas que se encuentran detrás de él.
ID:(12552, 0)
Ecuación de movimiento caida en medio viscoso
Ecuación
La fuerza con masa constante ($F$) es igual a la fuerza gravitacional ($F_g$) menos la fuerza viscosa ($F_v$) por lo que:
| $ F = F_g - F_v $ |
Esta relación permite establecer la ecuación de movimiento para la aceleración instantanea ($a$) con una masa inercial ($m_i$) que cae debido a la gravedad terrestre con la aceleración gravitacional ($g$), y con una masa gravitacional ($m_g$), en la constante de fuerza viscosa ($b$), tomará la forma de:
| $ m_i a = m_g g - b v $ |
ID:(14495, 0)
Ecuación diferencial para la caida en medio viscoso
Ecuación
La ecuación de movimiento para un cuerpo con la aceleración instantanea ($a$) y la masa inercial ($m_i$) que cae debido a la gravedad terrestre con una aceleración gravitacional ($g$), y con una masa gravitacional ($m_g$), en un medio viscoso con una constante de fuerza viscosa ($b$), se presenta de la siguiente manera:
| $ m_i a = m_g g - b v $ |
Para resolver esta ecuación, es necesario llevarla a su forma diferencial. Esto se logra reemplazando la aceleración instantanea ($a$) por la derivada de la velocidad ($v$) en el tiempo ($t$):
| $ m_i \displaystyle\frac{dv}{dt} = m_g g - b v $ |
ID:(14492, 0)
Tiempo de masa gravitacional y viscosidad
Ecuación
Con la ecuación de movimiento de un cuerpo en un medio viscoso, tenemos la derivada de la velocidad ($v$) en el tiempo ($t$) con la masa inercial ($m_i$), la masa gravitacional ($m_g$), la constante de fuerza viscosa ($b$) y la aceleración gravitacional ($g$):
| $ m_i \displaystyle\frac{dv}{dt} = m_g g - b v $ |
Lo que define la tiempo de viscosidad y masa gravitacional ($\tau_g$) como:
| $ \tau_g \equiv \displaystyle\frac{ m_g }{ b }$ |
ID:(15549, 0)
Tiempo de masa inercial y viscosidad
Ecuación
Con la ecuación de movimiento de un cuerpo en un medio viscoso, tenemos la derivada de la velocidad ($v$) en el tiempo ($t$) con la constante de fuerza viscosa ($b$) y la aceleración gravitacional ($g$):
| $ m_i \displaystyle\frac{dv}{dt} = - b v $ |
Lo que define la tiempo de viscosidad y masa inercial ($\tau_i$) como:
| $ \tau_i \equiv \displaystyle\frac{ m_i }{ b }$ |
ID:(15548, 0)
Solución de movimiento caida en medio viscoso
Ecuación
La ecuación de movimiento en la velocidad ($v$) en el tiempo ($t$) con la masa inercial ($m_i$), la masa gravitacional ($m_g$), la aceleración gravitacional ($g$) y la constante de fuerza viscosa ($b$):
| $ m_i \displaystyle\frac{dv}{dt} = m_g g - b v $ |
Suponiendo que el tiempo inicial es cero, la velocidad inicial ($v_0$), la tiempo de viscosidad y masa gravitacional ($\tau_g$) y la tiempo de viscosidad y masa inercial ($\tau_i$), obtenemos la siguiente ecuación:
| $ v = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
La ecuación de movimiento en la velocidad ($v$) en el tiempo ($t$) con la masa inercial ($m_i$), la masa gravitacional ($m_g$), la aceleración gravitacional ($g$) y la constante de fuerza viscosa ($b$):
| $ m_i \displaystyle\frac{dv}{dt} = m_g g - b v $ |
junto con la definición de la tiempo de viscosidad y masa inercial ($\tau_i$)
| $ \tau_i \equiv \displaystyle\frac{ m_i }{ b }$ |
y de la tiempo de viscosidad y masa gravitacional ($\tau_g$)
| $ \tau_g \equiv \displaystyle\frac{ m_g }{ b }$ |
puede ser reformulada como
$\displaystyle\frac{dv}{g\tau_g - v} = \displaystyle\frac{dt}{\tau_i}$
Si integramos esta expresión entre una velocidad inicial ($v_0$) y la velocidad ($v$), y desde el tiempo inicial nulo hasta el tiempo ($t$), obtenemos
$\ln(g\tau_g-v_0)-\ln(g\tau_g-v)=\displaystyle\frac{t}{\tau_i}$
Resolviendo para la velocidad, obtenemos
| $ v = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
Esta ecuación ilustra que la velocidad inicial ($v_0$) luego converge asintóticamente a la velocidad $g\tau_g$.
ID:(14493, 0)
Velocidad asintótica
Ecuación
La integración de la ecuación de movimiento arroja la velocidad ($v$) en función de la aceleración gravitacional ($g$), la tiempo de viscosidad y masa inercial ($\tau_i$), la tiempo de viscosidad y masa gravitacional ($\tau_g$), la velocidad inicial ($v_0$) y el tiempo ($t$) de la forma:
| $ v = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
Para el tiempo ($t$) mucho más grande que la tiempo de viscosidad y masa inercial ($\tau_i$), se obtiene el límite la velocidad asintótica ($v_{\infty}$):
| $ v_{\infty} \equiv g \tau_g $ |
ID:(14494, 0)
Ecuación diferencial camino en caída en medio viscoso
Ecuación
La integración de la ecuación de movimiento produce la velocidad ($v$) en términos de la aceleración gravitacional ($g$), la tiempo de viscosidad y masa inercial ($\tau_i$), la tiempo de viscosidad y masa gravitacional ($\tau_g$), la velocidad inicial ($v_0$) y el tiempo ($t$) de la siguiente manera:
| $ v = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
en su forma diferencial,
| $ \displaystyle\frac{ds}{dt} = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
donde la posición ($s$) representa la distancia recorrida.
ID:(14496, 0)
Camino recorrido en caída en medio viscoso
Ecuación
La integración de la ecuación de movimiento produce la posición ($s$) en términos de la aceleración gravitacional ($g$), la tiempo de viscosidad y masa inercial ($\tau_i$), la tiempo de viscosidad y masa gravitacional ($\tau_g$), la velocidad inicial ($v_0$) y el tiempo ($t$) de la siguiente manera:
| $ \displaystyle\frac{ds}{dt} = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
desde un tiempo inicial nulo hasta el tiempo ($t$), y desde la posición inicial ($s_0$) hasta la posición ($s$), obtenemos
| $ s = s_0 + g \tau_g t +( v_0 - g \tau_g ) \tau_i (1 - e^{- t / \tau_i })$ |
ID:(14497, 0)