User:
Viscous force and gravitation
Storyboard 
When an object moves through a viscous medium under the influence of a constant force like gravity, initially gravity accelerates the object until its velocity increases to a level where the viscous force and gravity balance out. From this point onward, the object no longer accelerates and moves at a constant velocity.
ID:(1965, 0)
Mechanisms
Iframe
Mechanisms
ID:(15539, 0)
Viscous force on a body
Top
The force experienced by a body moving at ($$) in a medium, characterized by the constant of the Viscose Force ($b$), is the viscose force ($F_v$), as described by the equation:
| $ F_v = b v $ |
To understand the role of the constant of the Viscose Force ($b$), it's important to remember that viscosity is a measure of how momentum, or the velocity of molecules, diffuses. In other words, the constant of the Viscose Force ($b$) represents the extent to which the body loses energy by transferring it to the medium and accelerating the molecules, thereby providing them with energy. Therefore, the constant of the Viscose Force ($b$) is proportional to viscosity.
ID:(15546, 0)
Forces on a sphere falling in a medium
Description
When a sphere is thrown into a viscous medium, there's an initial upward force, a gravitational Force ($F_g$), which gradually sinks the body. During this process, the sphere gains velocity, resulting in a downward force, a viscose force ($F_v$), which depends on the velocity. As the total velocity, the force with constant mass ($F$),
| $ F = F_g - F_v $ |
begins to decrease until it becomes null. From this moment on, the movement continues at a constant velocity since there's no force to accelerate it.
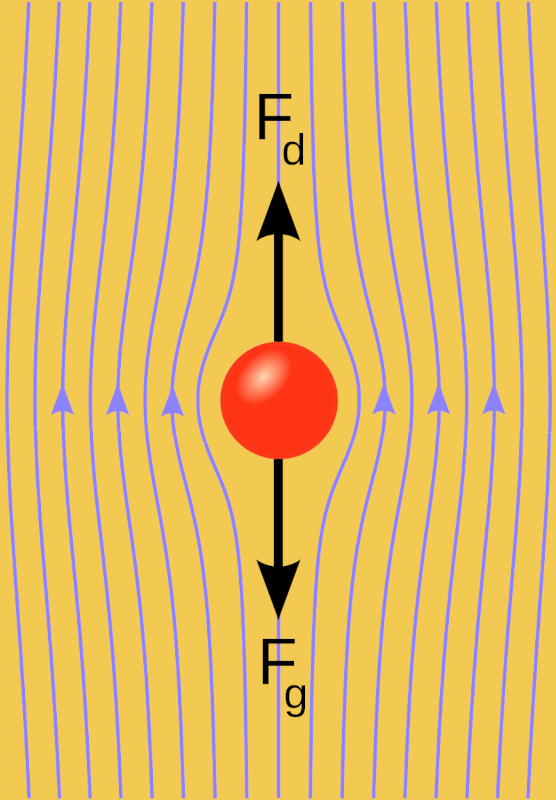
ID:(15544, 0)
Ostwald method for measuring viscosity
Description
The Ostwald viscosity measurement method is based on the behavior of a liquid flowing through a small-radius tube (capillary).
The liquid is introduced, suction is applied to exceed the upper mark, and then it is allowed to drain, measuring the time it takes for the level to pass from the upper to the lower mark.
The experiment is conducted first with a liquid for which viscosity and density are known (e.g., distilled water), and then with the liquid for which viscosity is to be determined. If conditions are identical, the liquid flowing in both cases will be similar, and thus, the time will be proportional to the density divided by the viscosity. Thus, a comparison equation between both viscosities can be established:
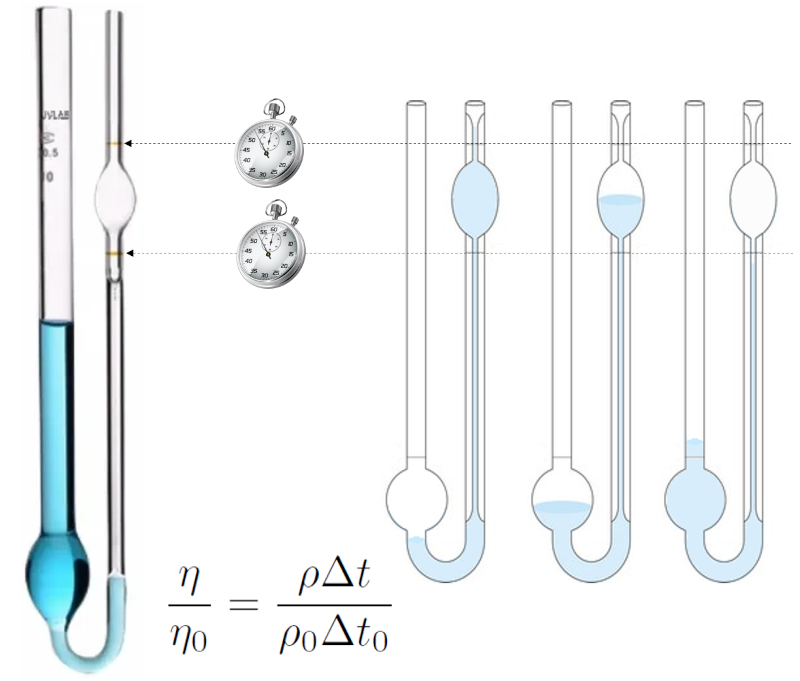
ID:(15545, 0)
Fall speed in viscous medium
Top
In the case of a body falling in a viscous medium, the equation of motion is an equation of the speed ($v$) as a function of the time ($t$) with the gravitational mass ($m_g$), the inertial Mass ($m_i$), the gravitational Acceleration ($g$), and the constant of the Viscose Force ($b$):
| $ m_i \displaystyle\frac{dv}{dt} = m_g g - b v $ |
This is obtained with the viscosity time and inertial mass ($\tau_i$)
| $ \tau_i \equiv \displaystyle\frac{ m_i }{ b }$ |
and with the viscosity time and gravitational mass ($\tau_g$)
| $ \tau_g \equiv \displaystyle\frac{ m_g }{ b }$ |
Integrating with initial time zero and the initial Speed ($v_0$),
| $ v = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
which is represented below:
The graph illustrates how viscosity compels the body to descend with ($$), which equals $g\tau_g$. This occurs at a time of the order of the viscosity time and inertial mass ($\tau_i$), whether the speed ($v$) is less than or greater than the asymptotic speed ($v_{\infty}$).
ID:(15547, 0)
Fall path in viscous medium
Top
In the case of a body falling in a viscous medium, the equation of motion is an equation of the position ($s$) as a function of the gravitational Acceleration ($g$), the viscosity time and inertial mass ($\tau_i$), the viscosity time and gravitational mass ($\tau_g$), the initial Speed ($v_0$), and the time ($t$):
| $ \displaystyle\frac{ds}{dt} = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
From this equation, we obtain by integrating with initial time zero and ($$):
| $ s = s_0 + g \tau_g t +( v_0 - g \tau_g ) \tau_i (1 - e^{- t / \tau_i })$ |
which is represented below:
ID:(15550, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ \displaystyle\frac{ds}{dt} = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$
@DIFF( s , t )= g * tau_g + ( v_0 - g * tau_g )*exp(- t / tau_i )
$ F = F_g - F_v $
F = F_g - F_v
$ F = m_i a $
F = m_i * a
$ F_g = m_g g $
F_g = m_g * g
$ F_v = b v $
F_v = b * v
$ m_g = m_i $
m_g = m_i
$ m_i \displaystyle\frac{dv}{dt} = m_g g - b v $
m_i * @DIFF( v , t ) = m_g * g - b * v
$ m_i a = m_g g - b v $
m_i * a = m_g * g - b * v
$ s = s_0 + g \tau_g t +( v_0 - g \tau_g ) \tau_i (1 - e^{- t / \tau_i })$
s = s_0 + g * tau_g * t + ( v_0 - g * tau_g )* tau_i *(1-exp(- t / tau_i ))
$ \tau_g \equiv \displaystyle\frac{ m_g }{ b }$
tau_g = m_g / b
$ \tau_i \equiv \displaystyle\frac{ m_i }{ b }$
tau_i = m_i / b
$ v = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$
v = g * tau_g + ( v_0 - g * tau_g )*exp(- t / tau_i )
$ v_{\infty} \equiv g \tau_g $
v_i = g * tau_g
ID:(15541, 0)
Total force of body falling in viscous medium
Equation
In the case of a body falling in a viscous medium, the total force, the force with constant mass ($F$), is equal to the gravitational Force ($F_g$) minus the viscose force ($F_v$), so
| $ F = F_g - F_v $ |
ID:(15543, 0)
Force case constant mass
Equation
In the case where the inertial Mass ($m_i$) equals the initial mass ($m_0$),
| $ m_g = m_i $ |
the derivative of momentum will be equal to the mass multiplied by the derivative of the speed ($v$). Since the derivative of velocity is the instant acceleration ($a$), we have that the force with constant mass ($F$) is
| $ F = m_i a $ |
Since the moment ($p$) is defined with the inertial Mass ($m_i$) and the speed ($v$),
| $ p = m_i v $ |
If the inertial Mass ($m_i$) is equal to the initial mass ($m_0$), then we can derive the momentum with respect to time and obtain the force with constant mass ($F$):
$F=\displaystyle\frac{d}{dt}p=m_i\displaystyle\frac{d}{dt}v=m_ia$
Therefore, we conclude that
| $ F = m_i a $ |
ID:(10975, 0)
Viscose Force
Equation
The simplest form of the viscose force ($F_v$) is one that is proportional to the the speed ($v$) of the body, represented by:
| $ F_v = b v $ |
The proportionality constant, also known as the constant of the Viscose Force ($b$), generally depends on the shape of the object and the viscosity of the medium through which it moves. An example of this type of force is the one exerted by a fluid stream on a spherical body, whose mathematical expression is known as Stokes' law.
ID:(3243, 0)
Gravitational Force
Equation
The gravitational Force ($F_g$) is based on the gravitational mass ($m_g$) of the object and on a constant reflecting the intensity of gravity at the planet's surface. The latter is identified by the gravitational Acceleration ($g$), which is equal to $9.8 m/s^2$.
Consequently, it is concluded that:
| $ F_g = m_g g $ |
ID:(3241, 0)
Equality of inertial and gravitational mass
Equation
The masses that Newton used in his principles are related to the inertia of bodies, which leads to the concept of the inertial Mass ($m_i$).
Newton's law, which is linked to the force between bodies due to their masses, is related to gravity, hence known as the gravitational mass ($m_g$).
Empirically, it has been concluded that both masses are equivalent, and therefore, we define
| $ m_g = m_i $ |
Einstein was the one who questioned this equality and, from that doubt, understood why both 'appear' equal in his theory of gravity. In his argument, Einstein explained that masses deform space, and this deformation of space causes a change in the behavior of bodies. Thus, masses turn out to be equivalent. The revolutionary concept of space curvature implies that even light, which lacks mass, is affected by celestial bodies, contradicting Newton's theory of gravitation. This was experimentally demonstrated by studying the behavior of light during a solar eclipse. In this situation, light beams are deflected due to the presence of the sun, allowing stars behind it to be observed.
ID:(12552, 0)
Equation of motion falling in a viscous medium
Equation
The force with constant mass ($F$) equals the gravitational Force ($F_g$) minus the viscose force ($F_v$) so that:
| $ F = F_g - F_v $ |
This relation allows establishing the motion equation for the instant acceleration ($a$) with ($$) falling due to Earth's gravity with the gravitational Acceleration ($g$), and with ($$), in the constant of the Viscose Force ($b$), it will take the form of:
| $ m_i a = m_g g - b v $ |
ID:(14495, 0)
Differential equation for the fall in a viscous medium
Equation
The inertial Mass ($m_i$) falling due to Earth's gravity with ($$), and with ($$) in a viscous medium with ($$), is presented as follows:
| $ m_i a = m_g g - b v $ |
To solve this equation, it is necessary to bring it to its differential form. This is achieved by replacing the instant acceleration ($a$) with the derivative of the speed ($v$) in the time ($t$):
| $ m_i \displaystyle\frac{dv}{dt} = m_g g - b v $ |
ID:(14492, 0)
Gravitational mass time and viscosity
Equation
With the equation of motion of a body in a viscous medium, we have the derivative of the speed ($v$) at the time ($t$) with the inertial Mass ($m_i$), the gravitational mass ($m_g$), the constant of the Viscose Force ($b$) and the gravitational Acceleration ($g$):
| $ m_i \displaystyle\frac{dv}{dt} = - b v $ |
This defines the viscosity time and gravitational mass ($\tau_g$) as:
| $ \tau_g \equiv \displaystyle\frac{ m_g }{ b }$ |
ID:(15549, 0)
Inertial mass time and viscosity
Equation
With the equation of motion of a body in a viscous medium, we have the derivative of the speed ($v$) at the time ($t$) with the constant of the Viscose Force ($b$) and the gravitational Acceleration ($g$):
| $ m_i \displaystyle\frac{dv}{dt} = - b v $ |
This defines the viscosity time and inertial mass ($\tau_i$) as:
| $ \tau_i \equiv \displaystyle\frac{ m_i }{ b }$ |
ID:(15548, 0)
Solution of motion falling in a viscous medium
Equation
The equation of motion in the speed ($v$) at the time ($t$) with the inertial Mass ($m_i$), the gravitational mass ($m_g$), the gravitational Acceleration ($g$), and the constant of the Viscose Force ($b$):
| $ m_i \displaystyle\frac{dv}{dt} = m_g g - b v $ |
Assuming the initial time is zero, the initial Speed ($v_0$), the viscosity time and gravitational mass ($\tau_g$), and the viscosity time and inertial mass ($\tau_i$), we obtain the following equation:
| $ v = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
The equation of motion at the speed ($v$) in the time ($t$) with the inertial Mass ($m_i$), the gravitational mass ($m_g$), the gravitational Acceleration ($g$), and the constant of the Viscose Force ($b$):
| $ m_i \displaystyle\frac{dv}{dt} = m_g g - b v $ |
along with the definition of the viscosity time and inertial mass ($\tau_i$)
| $ \tau_i \equiv \displaystyle\frac{ m_i }{ b }$ |
and the viscosity time and gravitational mass ($\tau_g$)
| $ \tau_g \equiv \displaystyle\frac{ m_g }{ b }$ |
can be reformulated as
$\displaystyle\frac{dv}{g\tau_g - v} = \displaystyle\frac{dt}{\tau_i}$
If we integrate this expression between ($$) and the speed ($v$), and from the initial time zero until the time ($t$), we obtain
$\ln(g\tau_g-v_0)-\ln(g\tau_g-v)=\displaystyle\frac{t}{\tau_i}$
Solving for velocity, we get
| $ v = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
This equation illustrates that the initial Speed ($v_0$) then asymptotically converges to the velocity $g\tau_g$.
ID:(14493, 0)
Asymptotic speed
Equation
The integration of the equation of motion yields the speed ($v$) as a function of the gravitational Acceleration ($g$), the viscosity time and inertial mass ($\tau_i$), the viscosity time and gravitational mass ($\tau_g$), the initial Speed ($v_0$) and the time ($t$) in the form:
| $ v = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
For the time ($t$) much larger than the viscosity time and inertial mass ($\tau_i$), the limit the asymptotic speed ($v_{\infty}$) is obtained:
| $ v_{\infty} \equiv g \tau_g $ |
ID:(14494, 0)
Differential equation falling path in viscous medium
Equation
The integration of the equation of motion yields the speed ($v$) as a function of the gravitational Acceleration ($g$), the viscosity time and inertial mass ($\tau_i$), the viscosity time and gravitational mass ($\tau_g$), the initial Speed ($v_0$) and the time ($t$) in the form:
| $ v = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
in its differential form,
| $ \displaystyle\frac{ds}{dt} = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
where the position ($s$) represents the distance traveled.
ID:(14496, 0)
Path traveled in a fall in a viscous medium
Equation
The integration of the equation of motion yields the position ($s$) in terms of the gravitational Acceleration ($g$), the viscosity time and inertial mass ($\tau_i$), the viscosity time and gravitational mass ($\tau_g$), the initial Speed ($v_0$) and the time ($t$) as follows:
| $ \displaystyle\frac{ds}{dt} = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
from an initial null time to the time ($t$), and from the starting position ($s_0$) to the position ($s$), we obtain
| $ s = s_0 + g \tau_g t +( v_0 - g \tau_g ) \tau_i (1 - e^{- t / \tau_i })$ |
ID:(14497, 0)