Kondensatoren
Storyboard 
Kondensatoren sind Elemente, mit denen Schaltkreise Ladung dynamisch speichern können. Sie sind bestäubt und können sich entladen, je nachdem, wie Potentiale angelegt werden, die Ladungen auf ihre Platten laden oder entladen.
ID:(1579, 0)
Kondensatoren Beispiel
Definition 
Los capacitores son elementos que se reconocen por tener
• dos contactos (cuidado la mayoría tiene dos)
• ser un cilindro o un bulto
Por problemas de disipar calor y no interferir por las cargas que almacena por lo general no esta integrado en el circuito y sobresale:

ID:(11703, 0)
Kapazitätseinheiten
Bild 
La capacidad se define como la relación entre la carga y el potencial eléctrico:
| $ \Delta\varphi =\displaystyle\frac{ Q }{ C }$ |
El primero se mide en Coulomb, el segundo en Volt. La división de Coulomb [C] por Volt [V] se denomina el Farad en honor a Michael Faraday.
Sin embargo la capacidad que se usa habitualmente es mucho mas chica que el Farad [F] por lo que los condensadores se indican en micro, nano y picofaradios:
| Microfarad $\mu F$ | $10^{-6} F$ |
| Nanofarad $nF$ | $10^{-9} F$ |
| Picofarad $pF$ | $10^{-12} F$ |
El Farad es MKS, micro, nano y pico Farad no.
ID:(11714, 0)
Schaltplan
Notiz 
Este es un circuito para una sirena. En el se reconocen en particular
• capacitores (dos rayas paralelas de mismo largo)
• resistencias (un rectángulo alargado)
• transistores (un triangulo con tres conectores)
• procesadores (cajas rectangulares con números)
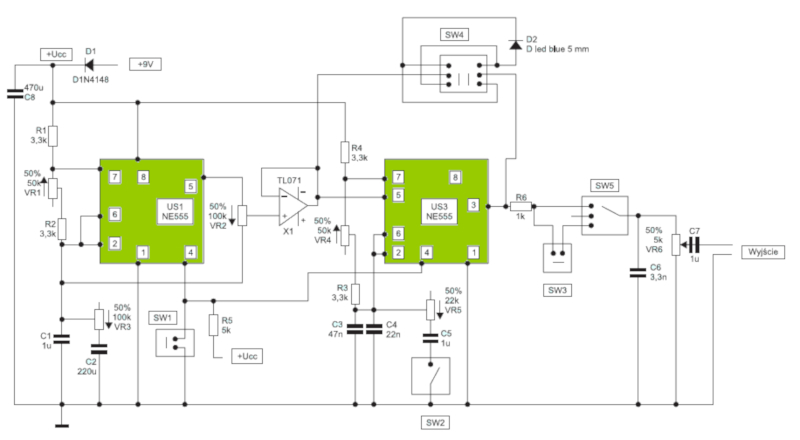
ID:(11704, 0)
Beispiel einer gedruckten Schaltung
Zitat 
Este es un circuito impreso, es decir se generaron las conexiones entre los elementos con métodos fotoquimicos. En el se reconocen en particular
• capacitores (dos rayas paralelas de mismo largo)
• resistencias (un rectángulo alargado)
• procesadores (cajas rectangulares con números)

ID:(11705, 0)
Parallele Platten, Geometrie
Übung 
Dos placas paralelas con un dieléctrico entre ellos forman un condensador:
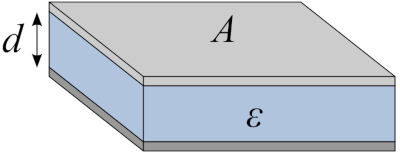
ID:(11706, 0)
Konzentrische Zylinder, Geometrie
Gleichung 
Dos cilindros concentricos con un dieléctrico entre ellos forman un condensador:
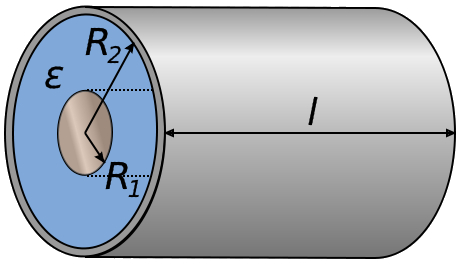
ID:(11707, 0)
Konzentrische Kugeln, Geometrie
Script 
Dos esferas concentricas con un dieléctrico entre ellas forman un condensador:

ID:(11709, 0)
Parallele Drähte, Geometrie
Variable 
Dos alambres pueden formar entre ellos un condensador:

Esto puede ser también involuntario.
ID:(11708, 0)
Kondensatoren
Beschreibung 
Kondensatoren sind Elemente, mit denen Schaltkreise Ladung dynamisch speichern können. Sie sind bestäubt und können sich entladen, je nachdem, wie Potentiale angelegt werden, die Ladungen auf ihre Platten laden oder entladen.
Variablen
Berechnungen
Berechnungen
Gleichungen
None
(ID 3218)
Beispiele
Al conectar capacidades en paralelo ca da de potencial
$Q=\displaystyle\sum_i Q_i$
Si ahora se aplica la relaci n de las capacidades para cada una de estas se tendr para potenciales iguales que
$\Delta\varphi=\displaystyle\frac{Q_i}{C_i}$
Con ello la carga total es igual a
$Q=\displaystyle\sum_i C_i\Delta\varphi$
por lo que la regla de suma de capacidades en paralelo ser con
| $ C_p =\displaystyle\sum_ i C_i $ |
(ID 3218)
Los capacitores son elementos que se reconocen por tener
• dos contactos (cuidado la mayor a tiene dos)
• ser un cilindro o un bulto
Por problemas de disipar calor y no interferir por las cargas que almacena por lo general no esta integrado en el circuito y sobresale:

(ID 11703)
La capacidad se define como la relaci n entre la carga y el potencial el ctrico:
| $ \Delta\varphi =\displaystyle\frac{ Q }{ C }$ |
El primero se mide en Coulomb, el segundo en Volt. La divisi n de Coulomb [C] por Volt [V] se denomina el Farad en honor a Michael Faraday.
Sin embargo la capacidad que se usa habitualmente es mucho mas chica que el Farad [F] por lo que los condensadores se indican en micro, nano y picofaradios:
| Microfarad $\mu F$ | $10^{-6} F$ |
| Nanofarad $nF$ | $10^{-9} F$ |
| Picofarad $pF$ | $10^{-12} F$ |
El Farad es MKS, micro, nano y pico Farad no.
(ID 11714)
Este es un circuito para una sirena. En el se reconocen en particular
• capacitores (dos rayas paralelas de mismo largo)
• resistencias (un rect ngulo alargado)
• transistores (un triangulo con tres conectores)
• procesadores (cajas rectangulares con n meros)

(ID 11704)
Este es un circuito impreso, es decir se generaron las conexiones entre los elementos con m todos fotoquimicos. En el se reconocen en particular
• capacitores (dos rayas paralelas de mismo largo)
• resistencias (un rect ngulo alargado)
• procesadores (cajas rectangulares con n meros)

(ID 11705)
Dos placas paralelas con un diel ctrico entre ellos forman un condensador:

(ID 11706)
La capacidad de un capacitor formado por dos placas paralelas es con igual a
| $ C_p = \displaystyle\frac{ \epsilon \epsilon_0 S }{ d }$ |
(ID 11713)
Dos cilindros concentricos con un diel ctrico entre ellos forman un condensador:

(ID 11707)
La capacidad de un capacitor formado por dos cilindros concentricos es con
| $ C_c = \displaystyle\frac{2 \pi \epsilon \epsilon_0 L }{\ln\left(\displaystyle\frac{ R_2 }{ R_1 }\right)}$ |
(ID 11711)
Dos esferas concentricas con un diel ctrico entre ellas forman un condensador:

(ID 11709)
La capacidad de un capacitor formado por dos esferas concentricas es con
| $ C_s = \displaystyle\frac{4 \pi \epsilon \epsilon_0 }{\displaystyle\frac{ 1 }{ R_1 }-\displaystyle\frac{ 1 }{ R_2 }}$ |
(ID 11712)
Dos alambres pueden formar entre ellos un condensador:

Esto puede ser tambi n involuntario.
(ID 11708)
La capacidad de un capacitor formado por dos alambres es con igual a
| $ C_w = \displaystyle\frac{ \pi \epsilon \epsilon_0 L }{arccosh\left(\displaystyle\frac{ d }{2 a }\right)}$ |
(ID 11710)
ID:(1579, 0)
