Utilizador:
Esfera em escoamento turbulento
Storyboard 
À medida que a velocidade do fluido ao redor de uma esfera aumenta, começam a se formar vórtices atrás dela, fazendo com que o fluxo se torne turbulento. Dessa forma, o fluxo passa de laminar a turbulento, levando a uma variação no coeficiente de resistência em função da velocidade.
ID:(462, 0)
Coeficiente de resistência hidráulica
Conceito
O coeficiente de resistência ($C_W$) varia em função de o número de Reynolds ($Re$) da seguinte maneira:
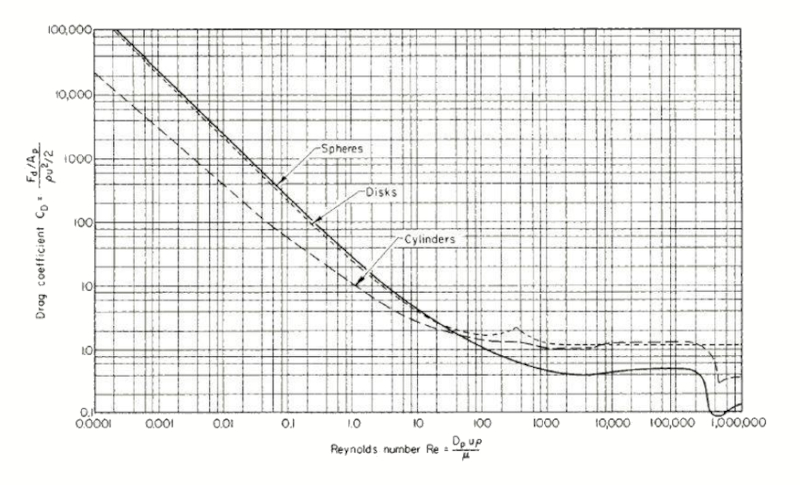
que pode ser estimada pela equação empírica:
| $ C_W = \displaystyle\frac{24}{ Re }(1 + 0.15 Re ^{0.687})$ |
Assim, la força de resistência ($F_W$) pode ser calculado usando la densidade ($\rho$), o perfil total do objeto ($S_p$) e la velocidade em relação ao meio ($v$) por meio de:
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
ID:(7065, 0)
Evolução da turbulência de acordo com o número de Reynold
Conceito
O comportamento do fluxo ao redor de uma esfera sofre mudanças dramáticas dependendo de o número de Reynolds ($Re$), que é calculado em função de la dimensão típica do sistema ($R$), que neste caso corresponde ao raio da esfera. Além disso, o número de Reynolds ($Re$) é uma função de la velocidade média do fluido ($v$), la densidade ($\rho$) e la viscosidade ($\eta$), conforme:
| $ Re =\displaystyle\frac{ \rho R v }{ \eta }$ |
o número de Reynolds ($Re$) expressa a proporção entre a inércia e a viscosidade do sistema. Quando a viscosidade domina, o fluxo tem um comportamento laminar, enquanto que, no caso oposto, a inércia prevalece. No primeiro caso, o meio tem tempo para se adaptar, enquanto no segundo, não há tempo suficiente, resultando na formação de vórtices ou até mesmo em um comportamento caótico.
O diagrama a seguir resume os diferentes comportamentos do fluxo:
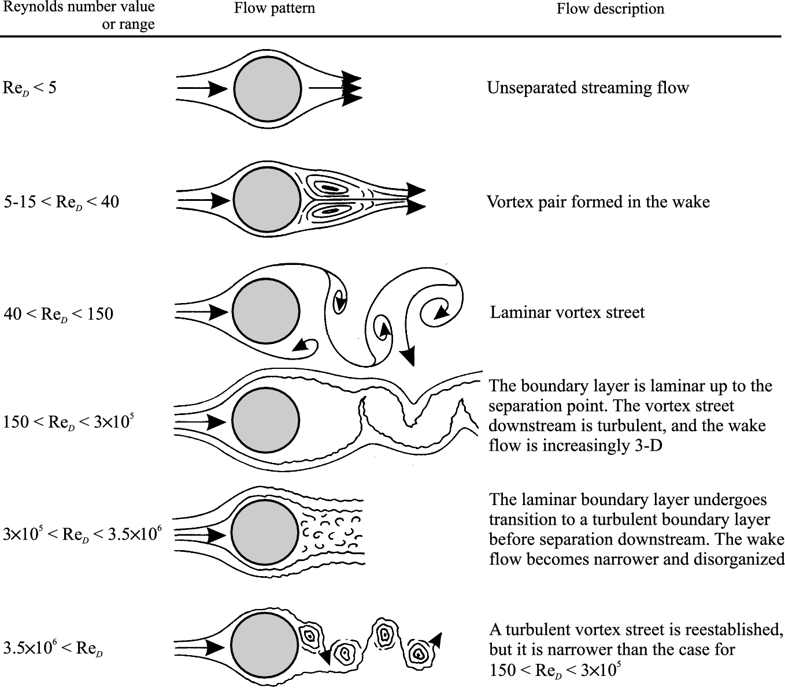
ID:(1890, 0)
Esfera de Fluxo; Re entre 5 e 40
Descrição
Quando o número de Reynolds ($Re$) está entre 5 e 40, o fluxo apresenta a formação de dois vórtices atrás da esfera:
ID:(11058, 0)
Esfera de Fluxo; Re entre 40 e 150
Descrição
Quando o número de Reynolds ($Re$) está entre 40 e 150, o fluxo apresenta a formação de vórtices alternados, criando o que é conhecido como uma rua de vórtices de Karman:
ID:(11059, 0)
Esfera de Fluxo; Re entre 150 e 3E+5
Descrição
Quando o número de Reynolds ($Re$) está entre 150 e 3E+5, o fluxo apresenta um nível significativo de caos dentro de uma estrutura macroscópica:
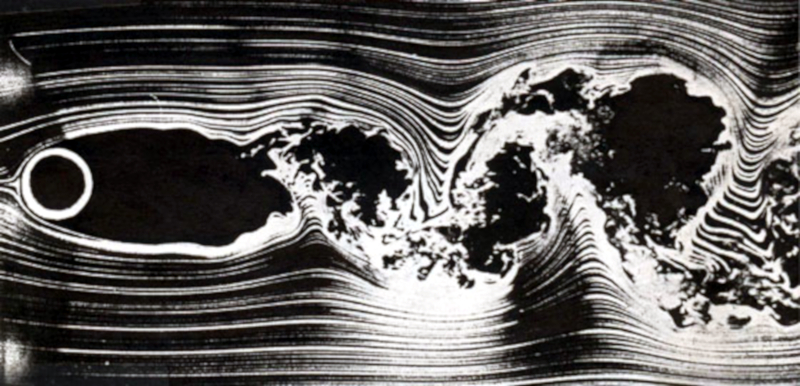
ID:(11060, 0)
Esfera de Fluxo; D maior que 3E+5
Descrição
Quando o número de Reynolds ($Re$) ultrapassa 3E+5, começa a se formar uma zona caótica atrás da esfera onde os vórtices já não são reconhecíveis (ou têm dimensões muito pequenas).
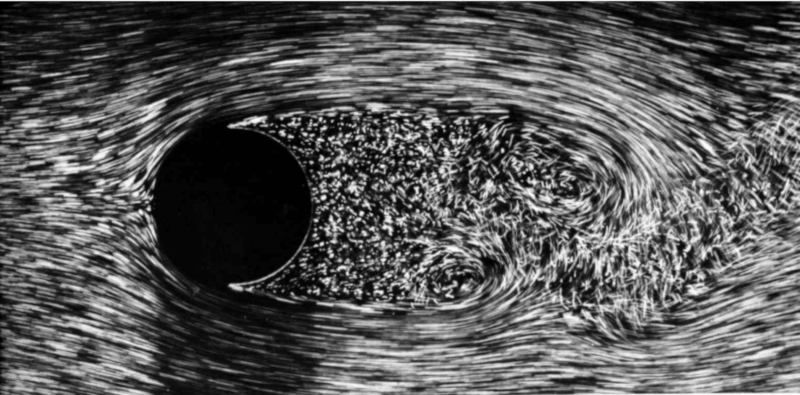
ID:(11061, 0)
Modelo
Top
Parâmetros
Variáveis
Cálculos
para 
, depois, selecione a variável: 
para 
Cálculos
Cálculos
Variáve 
Dado Calcular 
Objetivo : Equação A ser usado 
Equações
$ C_W = \displaystyle\frac{24}{ Re }(1 + 0.15 Re ^{0.687})$
C_W =24*(1+ Re ^0.687)/ Re
$ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$
F_W = rho * S_p * C_W * v ^2/2
$ Re =\displaystyle\frac{ \rho R v }{ \eta }$
Re = rho * R * v / eta
ID:(15899, 0)
Número de Reynolds
Equação
O critério chave para determinar se um meio é laminar ou turbulento é o chamado número de Reynolds, que compara a energia associada à inércia com aquela associada à viscosidade. A primeira depende de la densidade ($\rho$), la velocidade média do fluido ($v$) e la dimensão típica do sistema ($R$), enquanto a segunda depende de la viscosidade ($\eta$), definindo-o como:
| $ Re =\displaystyle\frac{ \rho R v }{ \eta }$ |
ID:(3177, 0)
Coeficiente de arrasto de uma esfera
Equação
Empiricamente, o coeficiente de resistência ($C_W$) pode ser modelado em função de o número de Reynolds ($Re$) da seguinte maneira:
| $ C_W = \displaystyle\frac{24}{ Re }(1 + 0.15 Re ^{0.687})$ |
ID:(15900, 0)
Força de resistência
Equação
La força de resistência ($F_W$) pode ser calculado usando la densidade ($\rho$), o coeficiente de resistência ($C_W$), o perfil total do objeto ($S_p$) e la velocidade em relação ao meio ($v$) de acordo com o seguinte fórmula:
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
De maneira semelhante à forma como a equação para la força de elevação ($F_L$) foi obtida utilizando la densidade ($\rho$), o coeficiente de elevação ($C_L$), la superfície que gera sustentação ($S_w$) e la velocidade em relação ao meio ($v$)
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
nesta analogia, o que corresponde a la superfície que gera sustentação ($S_w$) será equivalente a o perfil total do objeto ($S_p$) e o coeficiente de elevação ($C_L$) a o coeficiente de resistência ($C_W$), resultando no cálculo de la força de resistência ($F_W$):
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
O coeficiente de arrasto é medido e, em fluxos turbulentos sobre corpos aerodinâmicos, geralmente se obtêm valores em torno de 0.4.
ID:(4418, 0)