Storyboard

Para manobrar um avião, é necessário orientá-lo na posição desejada para alterar a rota e/ou a altitude de voo. Para isso, o avião é equipado com ailerons nas pontas das asas, superfícies de controle nos estabilizadores traseiros e um leme na cauda, que geram forças. Essas forças, ao atuarem a uma certa distância do centro de massa, criam torques que permitem a rotação do avião em torno de seus diferentes eixos.

A magnitude da rotação depende dos momentos de inércia, sendo que o corpo da aeronave e as asas desempenham um papel importante. Portanto, é fundamental estimar esses momentos de inércia para prever como o avião responderá às manobras e garantir um controle preciso durante o voo.

>Modelo

ID:(2117, 0)

Descrição

>Top

Pode-se assumir que o centro de massa da aeronave está localizado no centro do fuselagem, na altura das asas. Portanto, o modelo mais simples para descrever sua dinâmica considera o fuselagem como um cilindro central e as asas como retângulos finos.

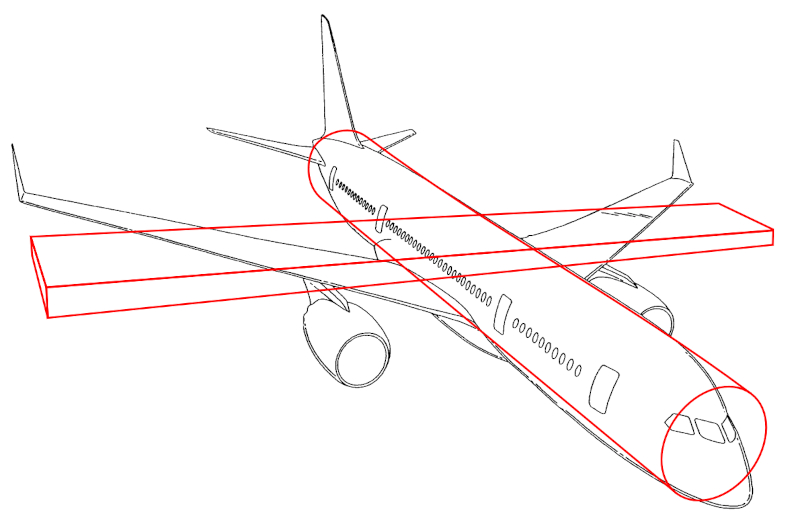
Numa primeira aproximação, o momento de inércia do corpo da aeronave em torno de seu eixo longitudinal pode ser desprezado, pois o momento de inércia das asas domina nas rotações ao redor deste eixo.

Da mesma forma, nos movimentos de arfagem, o momento de inércia das asas em relação ao seu próprio eixo pode ser inicialmente desconsiderado, uma vez que tem um efeito menor em comparação com outras forças.

Para um modelo mais refinado, podem ser adicionadas as contribuições desses momentos de inércia, juntamente com os três retângulos finos que representam o leme e os dois estabilizadores horizontais. Isso permitiria uma simulação mais precisa da dinâmica de voo da aeronave, especialmente em manobras mais complexas.

ID:(15983, 0)

Descrição

>Top

La massa da asa ($m_w$) pode ser aproximado como o volume de um paralelepípedo retângulo multiplicado pela densidade da aeronave:

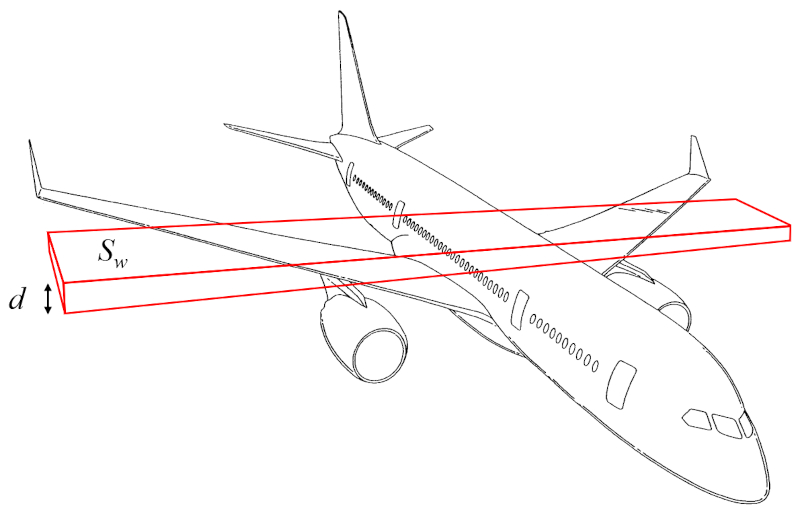
O volume, portanto, pode ser calculado a partir de la superfície que gera sustentação ($S_w$) e la altura da asa ($d$).

Assim, la massa da asa ($m_w$) é determinado utilizando o densidade corporal da aeronave ($\rho_a$), la superfície que gera sustentação ($S_w$) e la altura da asa ($d$), da seguinte maneira:

ID:(15989, 0)

Descrição

>Top

La massa corporal da aeronave ($m_p$) pode ser aproximado como o volume de um cilindro multiplicado pela densidade da aeronave:

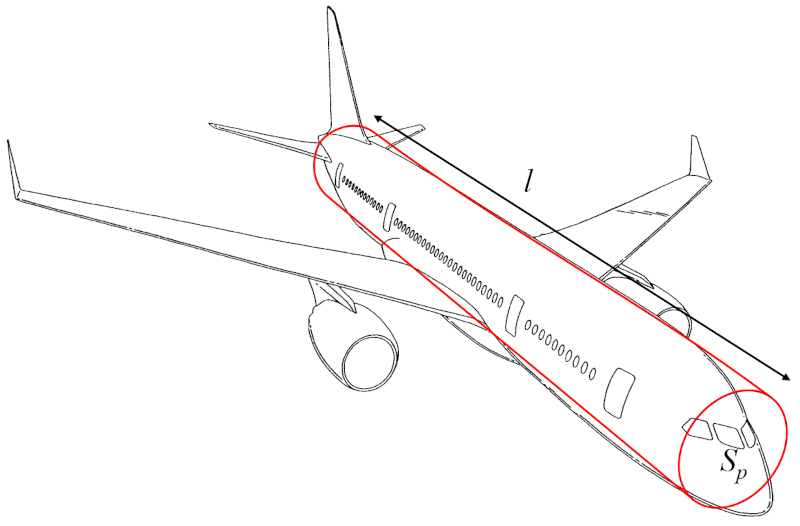
O volume, portanto, pode ser calculado usando o perfil total do objeto ($S_p$) (o raio ou diâmetro) e o distância ao longo da asa ($l$) (a altura do cilindro).

Assim, la massa corporal da aeronave ($m_p$) é determinado a partir de o densidade corporal da aeronave ($\rho_a$), o perfil total do objeto ($S_p$) e o distância ao longo da asa ($l$), da seguinte maneira:

ID:(15990, 0)

Descrição

>Top

O momento de inércia do eixo da asa ($I_e$) pode ser aproximado como o momento de inércia de um cilindro que representa o corpo da aeronave, rotacionando em torno de um eixo perpendicular ao eixo do cilindro, que é paralelo às asas:

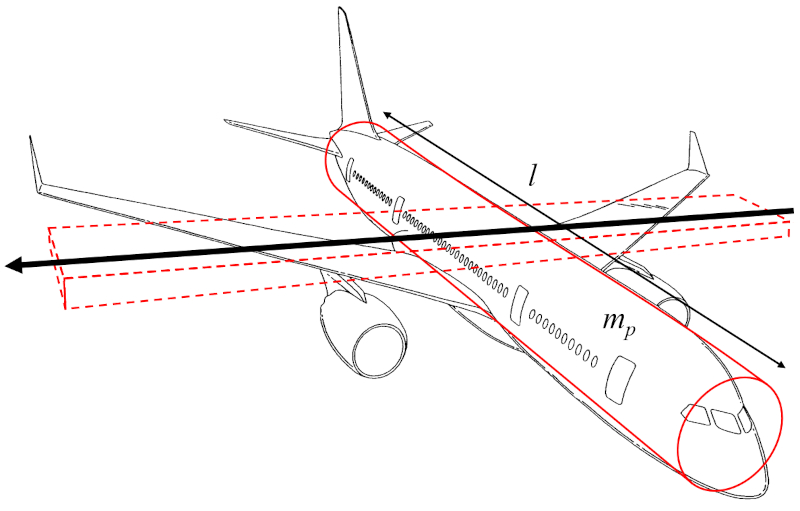
Como o largura da asa ($w$) é muito menor que o distância ao longo da asa ($l$), o termo envolvendo $w^2$ pode ser desprezado, focando apenas em la massa corporal da aeronave ($m_p$) e no termo com o distância ao longo da asa ($l$) ao quadrado.

Portanto, o momento de inércia do eixo da asa ($I_e$) é calculado a partir de la massa corporal da aeronave ($m_p$) e o distância ao longo da asa ($l$), da seguinte maneira:

$I_e = \displaystyle\frac{1}{12} m_p l ^2$

Condições

Variáveis

Relação

ID:(15991, 0)

Descrição

>Top

O momento de inércia do eixo vertical ($I_r$) pode ser aproximado como a soma do momento de inércia de um cilindro que representa o fuselagem da aeronave, rotacionando em torno de um eixo perpendicular ao seu eixo longitudinal, e o momento de inércia de um paralelepípedo retangular que representa as asas, rotacionando em torno de um eixo perpendicular a elas:

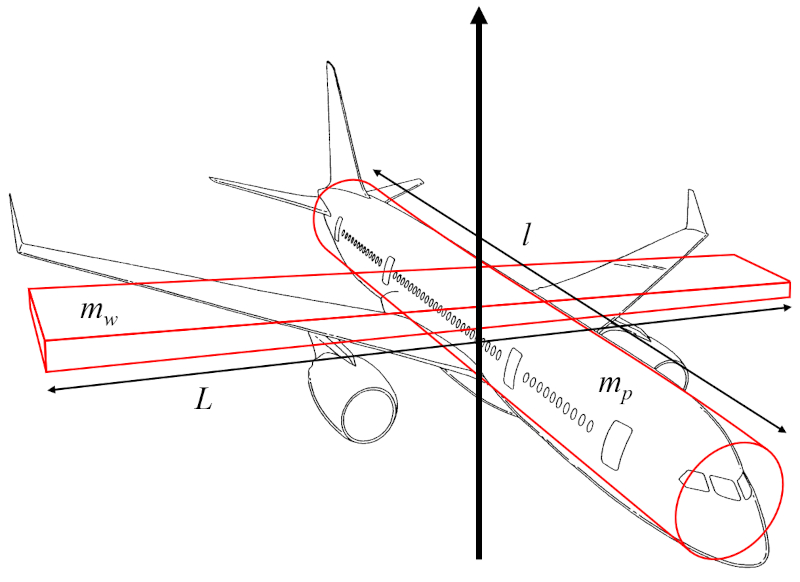
Se, para a estimativa de o momento de inércia do eixo vertical ($I_r$), for assumido que o raio do cilindro do fuselagem é muito menor que o distância ao longo da asa ($l$) e que o largura da asa ($w$) é muito menor que la envergadura das asas ($L$), o momento de inércia do cilindro depende principalmente de la massa corporal da aeronave ($m_p$) e o distância ao longo da asa ($l$), enquanto o momento de inércia do paralelepípedo depende de la massa da asa ($m_w$) e la envergadura das asas ($L$).

Portanto, o momento de inércia do eixo vertical ($I_r$) é calculado a partir de la massa corporal da aeronave ($m_p$), la massa da asa ($m_w$), ( $$)6337 ($$ )10333

$I_r = \displaystyle\frac{1}{12}( m_p l ^2 + m_w L ^2)$

Condições

Variáveis

Relação

ID:(15993, 0)

Descrição

>Top

O momento de inércia do eixo do avião ($I_a$) pode ser aproximado como o momento de inércia de um paralelepípedo retangular que representa a asa da aeronave, rotacionando em torno de um eixo paralelo à sua largura:

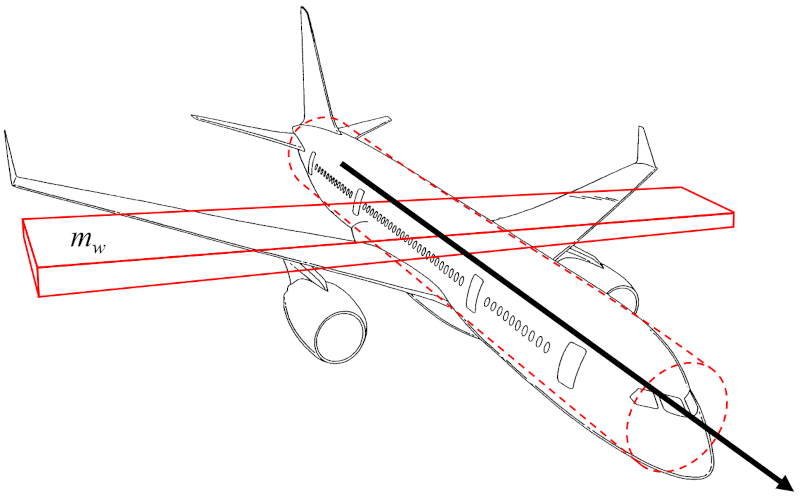
Como o corpo da aeronave é relativamente estreito, o momento de inércia do cilindro que o representa pode ser desprezado em uma primeira aproximação. Assim, o momento de inércia do eixo do avião ($I_a$) é proporcional a la massa da asa ($m_w$) e ao quadrado de la envergadura das asas ($L$).

Portanto, o momento de inércia do eixo do avião ($I_a$) é calculado a partir de la massa da asa ($m_w$) e la envergadura das asas ($L$), da seguinte forma:

$I_a = \displaystyle\frac{1}{6} m_w L ^2$

Condições

Variáveis

Relação

ID:(15992, 0)

Equação

>Top, >Modelo

La massa da asa ($m_w$) é calculado a partir de o densidade corporal da aeronave ($\rho_a$), la superfície que gera sustentação ($S_w$) e la altura da asa ($d$), da seguinte forma:

$m_w = \rho_a S_w d$

Condições

Variáveis

$d$

Altura da asa

$m$

6338

$\rho_a$

Densidade corporal da aeronave

$kg/m^3$

6220

$m_w$

Massa da asa

$kg$

6339

$S_w$

Superfície que gera sustentação

$m^2$

6117

Relação

ID:(15984, 0)

Equação

>Top, >Modelo

La massa corporal da aeronave ($m_p$) é calculado a partir de o densidade corporal da aeronave ($\rho_a$), o perfil total do objeto ($S_p$) e o distância ao longo da asa ($l$), da seguinte forma:

$m_p = \rho_a S_p l$

Condições

Variáveis

$l$

Comprimento do aeronave

$m$

10469

$\rho_a$

Densidade corporal da aeronave

$kg/m^3$

6220

$m_p$

Massa corporal da aeronave

$kg$

6340

$S_p$

Perfil total do objeto

$m^2$

6123

Relação

ID:(15985, 0)

Equação

>Top, >Modelo

La massa da asa ($m_w$) é calculado a partir de la massa corporal da aeronave ($m_p$) e ($$)10333

$I_e = \displaystyle\frac{1}{12} m_p l ^2$

Condições

Variáveis

$l$

Comprimento do aeronave

$m$

10469

$m_p$

Massa corporal da aeronave

$kg$

6340

$I_e$

Momento de inércia do eixo da asa

$kg m^2$

10220

Relação

ID:(15987, 0)

Equação

>Top, >Modelo

O momento de inércia do eixo vertical ($I_r$) é calculado a partir de la massa da asa ($m_w$), la envergadura das asas ($L$) e ($$)10333

$I_r = \displaystyle\frac{1}{12}( m_p l ^2 + m_w L ^2)$

Condições

Variáveis

$l$

Comprimento do aeronave

$m$

10469

$L$

Envergadura das asas

$m$

6337

$m_p$

Massa corporal da aeronave

$kg$

6340

$m_w$

Massa da asa

$kg$

6339

$I_r$

Momento de inércia do eixo vertical

$kg m^2$

10221

Relação

ID:(15988, 0)

Equação

>Top, >Modelo

O momento de inércia do eixo do avião ($I_a$) é calculado a partir de la massa da asa ($m_w$) e ($$)6337

$I_a = \displaystyle\frac{1}{6} m_w L ^2$

Condições

Variáveis

$L$

Envergadura das asas

$m$

6337

$m_w$

Massa da asa

$kg$

6339

$I_a$

Momento de inércia do eixo do avião

$kg m^2$

10219

Relação

ID:(15986, 0)