User:
Sphere in turbulent flow
Storyboard 
As the velocity of the fluid around a sphere increases, vortices begin to form behind it, causing the flow to become turbulent. In this way, the flow transitions from laminar to turbulent, leading to a variation in the drag coefficient as a function of velocity.
ID:(462, 0)
Coefficient of hydraulic resistance
Concept
The coefficient of resistance ($C_W$) varies as a function of the number of Reynold ($Re$) according to:
which can be estimated using the empirical equation:
| $ C_W = \displaystyle\frac{24}{ Re }(1 + 0.15 Re ^{0.687})$ |
Thus, the resistance force ($F_W$) can be calculated using the density ($\rho$), the total object profile ($S_p$), and the speed with respect to the medium ($v$) by:
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
ID:(7065, 0)
Turbulence evolution according to Reynold number
Concept
The behavior of the flow around a sphere undergoes dramatic changes depending on the number of Reynold ($Re$), which is calculated as a function of the typical Dimension of the System ($R$), corresponding in this case to the radius of the sphere. Additionally, the number of Reynold ($Re$) is a function of the mean Speed of Fluid ($v$), the density ($\rho$), and the viscosity ($\eta$) as follows:
| $ Re =\displaystyle\frac{ \rho R v }{ \eta }$ |
the number of Reynold ($Re$) expresses the ratio between the systems inertia and viscosity. When viscosity dominates, the flow exhibits laminar behavior, whereas when inertia dominates, the flow becomes turbulent. In the former case, the medium has time to adjust, while in the latter, the flow does not have enough time, resulting in the formation of vortices or even chaotic behavior.
The following diagram summarizes the different flow behaviors:
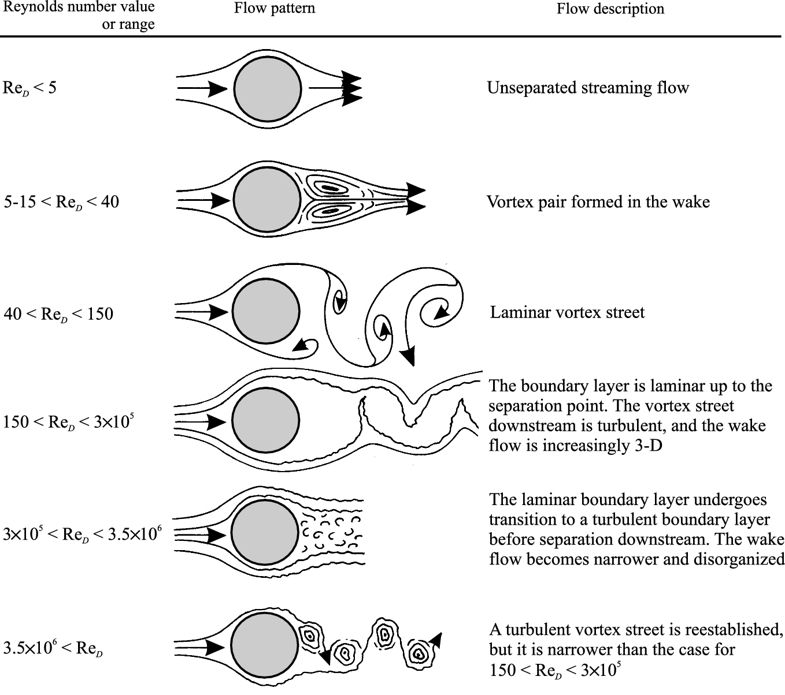
Flow type scheme according to Reynold number (book Introduction to Transport Phenomena Modeling, Gianpaolo Ruocco - https://link.springer.com/chapter/10.1007/978-3-319-66822-2_3)
ID:(1890, 0)
Flowing sphere; Re between 5 and 40
Description
When the number of Reynold ($Re$) is between 5 and 40 the flow shows two whirlwinds behind the sphere:
Flow around a sphere for Reynold number between 5 and 40 (https://aerospaceengineeringblog.com/how-quickly-do-gas-bubbles-rise-in-a-pint-of-beer/)
ID:(11058, 0)
Flowing sphere; Re between 40 and 150
Description
When the number of Reynold ($Re$) is between 40 and 150, the flow exhibits the formation of alternating vortices, creating what is known as a Karman vortex street:
Flow around a sphere for Reynold number between 40 and 150 (https://www.researchgate.net/publication/303369967_Experimental_investigation_of_low_mode_number_cylinders_subjected_to_vortex-induced_vibrations)
ID:(11059, 0)
Flowing sphere; Re between 150 and 3E+5
Description
When the number of Reynold ($Re$) is between 150 and 3E+5, the flow exhibits a significant level of turbulence within a macroscopic structure:
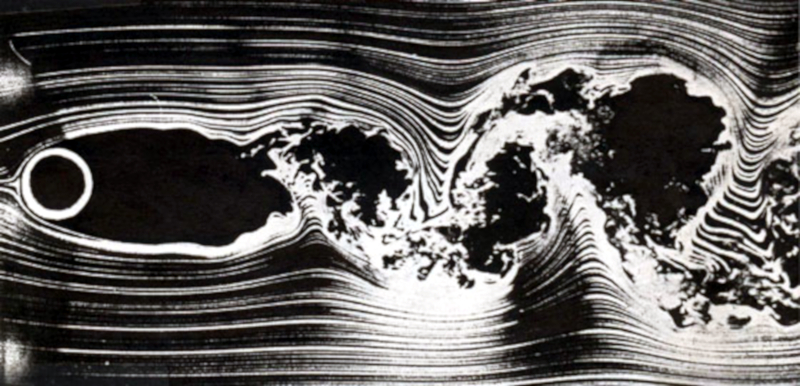
Flow around a sphere for Reynold number between 150 and 3E + 5 ()
ID:(11060, 0)
Flowing sphere; Re greater than 3E+5
Description
When the number of Reynold ($Re$) exceeds 3E+5, a chaotic zone begins to form behind the sphere, where vortices are no longer recognizable (or they have very small dimensions).
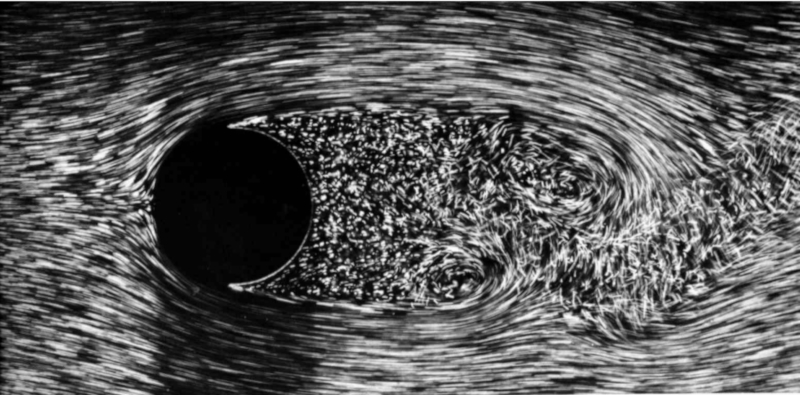
Flow around a sphere for Reynold number greater than 3E+5 (https://www.pinterest.cl/pin/514888169895997311/)
ID:(11061, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ C_W = \displaystyle\frac{24}{ Re }(1 + 0.15 Re ^{0.687})$
C_W =24*(1+ Re ^0.687)/ Re
$ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$
F_W = rho * S_p * C_W * v ^2/2
$ Re =\displaystyle\frac{ \rho R v }{ \eta }$
Re = rho * R * v / eta
ID:(15899, 0)
Reynold Number
Equation
The key criterion for determining whether a medium is laminar or turbulent is the Reynolds number, which compares the energy associated with inertia to that associated with viscosity. The former depends on the density ($\rho$), the mean Speed of Fluid ($v$), and the typical Dimension of the System ($R$), while the latter depends on the viscosity ($\eta$), defining it as:
| $ Re =\displaystyle\frac{ \rho R v }{ \eta }$ |
ID:(3177, 0)
Drag coefficient of a sphere
Equation
Empirically, the coefficient of resistance ($C_W$) can be modeled as a function of the number of Reynold ($Re$) as follows:
| $ C_W = \displaystyle\frac{24}{ Re }(1 + 0.15 Re ^{0.687})$ |
ID:(15900, 0)
Resistance force
Equation
The resistance force ($F_W$) kann mit the density ($\rho$), the coefficient of resistance ($C_W$), the total object profile ($S_p$) und the speed with respect to the medium ($v$) entsprechend berechnet werden folgende Formel:
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
Similarly to how the equation for the lift force ($F_L$) was derived using the density ($\rho$), the coefficient of lift ($C_L$), the surface that generates lift ($S_w$), and the speed with respect to the medium ($v$)
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
in this analogy, what corresponds to the surface that generates lift ($S_w$) will be equivalent to the total object profile ($S_p$) and the coefficient of lift ($C_L$) to the coefficient of resistance ($C_W$), thus the resistance force ($F_W$) is calculated:
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
The drag coefficient is measured and, in turbulent flows over aerodynamic bodies, values are generally found around 0.4.
ID:(4418, 0)