Utilisateur:
Sphère en écoulement turbulent
Storyboard 
À mesure que la vitesse du fluide autour d'une sphère augmente, des vortex commencent à se former derrière celle-ci, provoquant une transition vers un écoulement turbulent. Ainsi, le flux passe de laminaire à turbulent, entraînant une variation du coefficient de traînée en fonction de la vitesse.
ID:(462, 0)
Coefficient de résistance hydraulique
Concept
Le coefficient de résistance ($C_W$) varie en fonction de le le numéro de Reynold ($Re$) comme suit :
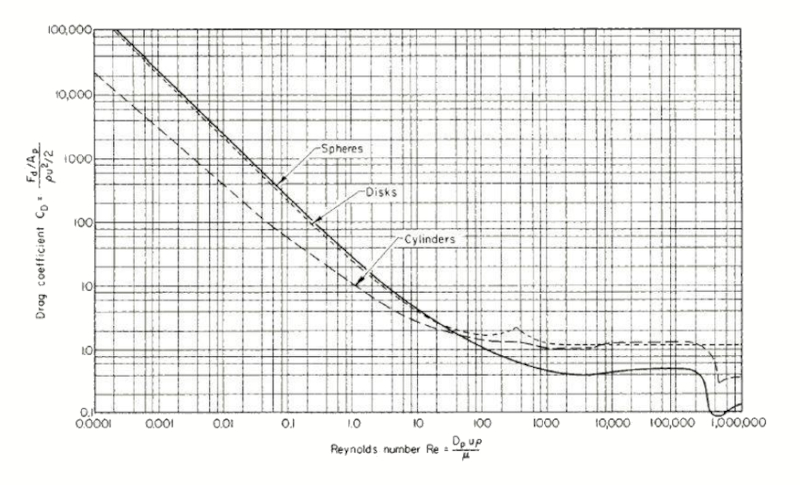
qui peut être estimé avec léquation empirique :
| $ C_W = \displaystyle\frac{24}{ Re }(1 + 0.15 Re ^{0.687})$ |
Ainsi, a force de résistance ($F_W$) peut être calculé avec a densité ($\rho$), le profil total de l'objet ($S_p$) et a vitesse par rapport au milieu ($v$) à laide de :
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
ID:(7065, 0)
Evolution de la turbulence selon le nombre de Reynold
Concept
Le comportement de lécoulement autour dune sphère change de manière drastique en fonction de le le numéro de Reynold ($Re$), calculé en fonction de a dimension typique du système ($R$), qui dans ce cas correspond au rayon de la sphère. De plus, le le numéro de Reynold ($Re$) est une fonction de a vitesse moyenne du fluide ($v$), a densité ($\rho$) et a viscosité ($\eta$), selon :
| $ Re =\displaystyle\frac{ \rho R v }{ \eta }$ |
le le numéro de Reynold ($Re$) exprime le rapport entre l'inertie et la viscosité du système. Lorsque la viscosité domine, lécoulement présente un comportement laminaire, tandis que lorsque l'inertie prend le dessus, l'écoulement devient turbulent. Dans le premier cas, le milieu a le temps de s'adapter, tandis que dans le second, le flux ne dispose pas de suffisamment de temps, ce qui entraîne la formation de vortex ou même un comportement chaotique.
Le diagramme suivant résume les différents comportements de lécoulement :
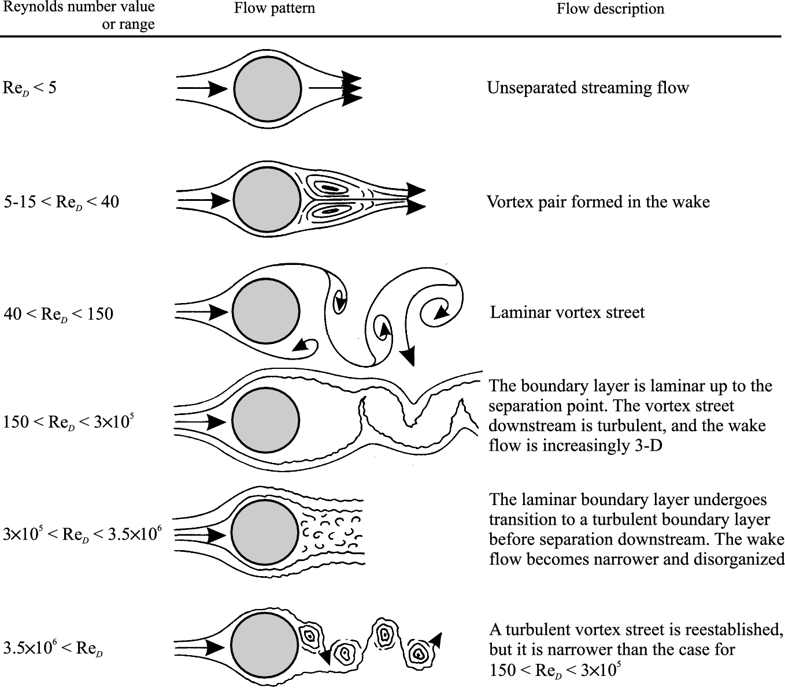
ID:(1890, 0)
Sphère de flux ; Re entre 5 et 40
Description
Lorsque le le numéro de Reynold ($Re$) est compris entre 5 et 40, l'écoulement montre la formation de deux tourbillons derrière la sphère:
ID:(11058, 0)
Sphère de flux ; Re entre 40 et 150
Description
Lorsque le le numéro de Reynold ($Re$) est compris entre 40 et 150, l'écoulement montre la formation de tourbillons alternatifs, créant ce que l'on appelle une rue de tourbillons de Karman:
ID:(11059, 0)
Sphère de flux ; Re entre 150 et 3E+5
Description
Lorsque le le numéro de Reynold ($Re$) se situe entre 150 et 3E+5, l'écoulement présente un niveau considérable de chaos au sein d'une structure macroscopique:
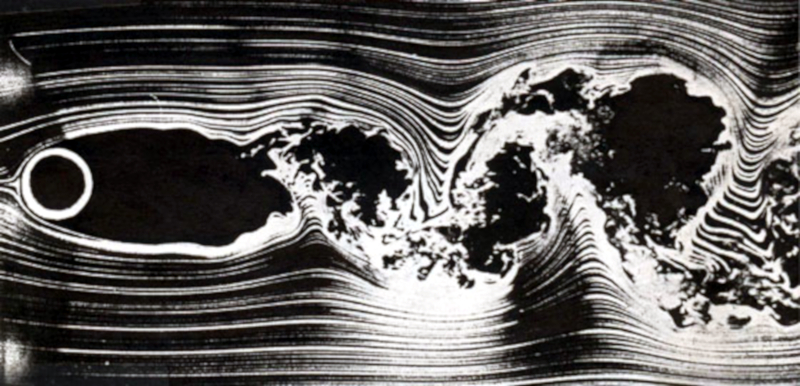
ID:(11060, 0)
Sphère de flux ; D supérieur à 3E+5
Description
Lorsque le le numéro de Reynold ($Re$) dépasse 3E+5, une zone chaotique commence à se former derrière la sphère où les tourbillons ne sont plus reconnaissables (ou ont des dimensions très réduites).
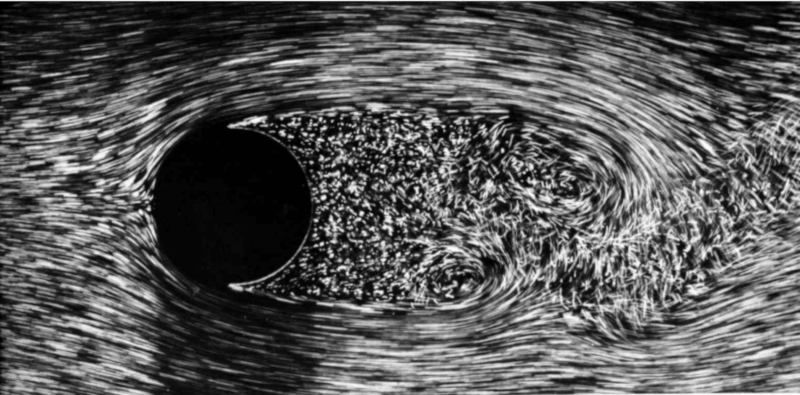
ID:(11061, 0)
Modèle
Top
Paramètres
Variables
Calculs
à 
, puis, sélectionnez la variable: 
à 
Calculs
Calculs
Variable 
Donnée Calculer 
Cible : Équation À utiliser 
Équations
$ C_W = \displaystyle\frac{24}{ Re }(1 + 0.15 Re ^{0.687})$
C_W =24*(1+ Re ^0.687)/ Re
$ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$
F_W = rho * S_p * C_W * v ^2/2
$ Re =\displaystyle\frac{ \rho R v }{ \eta }$
Re = rho * R * v / eta
ID:(15899, 0)
Le numéro de Reynold
Équation
Le critère clé pour déterminer si un milieu est laminé ou turbulent est le numéro de Reynolds, qui compare l'énergie associée à l'inertie à celle associée à la viscosité. La première dépend de a densité ($\rho$), a vitesse moyenne du fluide ($v$) et a dimension typique du système ($R$), tandis que la seconde dépend de a viscosité ($\eta$), le définissant ainsi :
| $ Re =\displaystyle\frac{ \rho R v }{ \eta }$ |
ID:(3177, 0)
Coefficient de traînée d'une sphère
Équation
Empiriquement, le coefficient de résistance ($C_W$) peut être modélisé en fonction de le le numéro de Reynold ($Re$) comme suit :
| $ C_W = \displaystyle\frac{24}{ Re }(1 + 0.15 Re ^{0.687})$ |
ID:(15900, 0)
Force de résistance
Équation
A force de résistance ($F_W$) peut être calculé en utilisant a densité ($\rho$), le coefficient de résistance ($C_W$), le profil total de l'objet ($S_p$) et a vitesse par rapport au milieu ($v$) selon le formule suivante :
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
De manière similaire à la façon dont l'équation pour a force de levage ($F_L$) a été dérivée en utilisant a densité ($\rho$), le coefficient de portance ($C_L$), a surface génératrice de portance ($S_w$) et a vitesse par rapport au milieu ($v$)
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
dans cette analogie, ce qui correspond à A surface génératrice de portance ($S_w$) sera équivalent à Le profil total de l'objet ($S_p$) et le coefficient de portance ($C_L$) à Le coefficient de résistance ($C_W$), ce qui permet de calculer a force de résistance ($F_W$) :
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
Le coefficient de traînée est mesuré et, dans les écoulements turbulents sur les corps aérodynamiques, les valeurs sont généralement autour de 0.4.
ID:(4418, 0)