Esfera en flujo turbulento
Storyboard 
A medida que la velocidad del fluido alrededor de una esfera aumenta, comienzan a formarse vórtices detrás de ella, lo que provoca que el flujo se vuelva turbulento. De esta manera, se transita de un flujo laminar a uno turbulento, lo que resulta en una variación del coeficiente de resistencia en función de la velocidad.
ID:(462, 0)
Coeficiente de resistencia hidraulica
Concepto 
El coeficiente de resistencia ($C_W$) varía en función de el número de Reynold ($Re$) según:
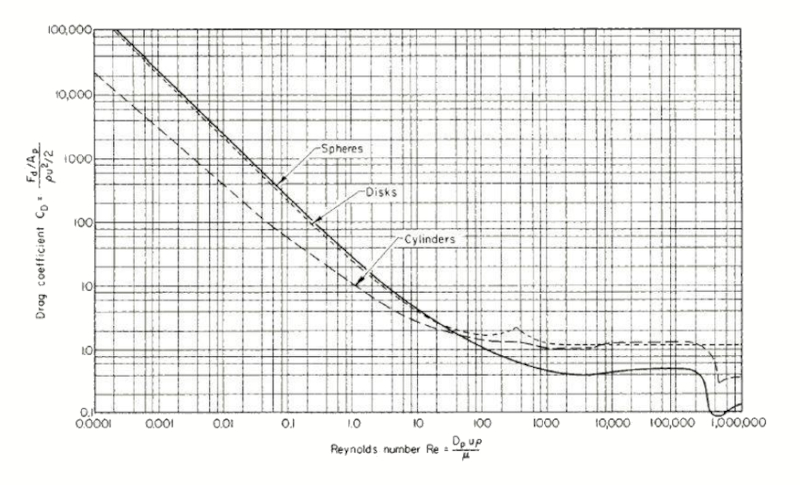
que se puede estimar con la ecuación empírica:
| $ C_W = \displaystyle\frac{24}{ Re }(1 + 0.15 Re ^{0.687})$ |
De este modo, la fuerza de resistencia ($F_W$) se puede calcular con la densidad ($\rho$), el perfil total del objeto ($S_p$) y la velocidad respecto del medio ($v$) mediante:
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
ID:(7065, 0)
Evolución de turbulencias según número Reynold
Concepto 
El comportamiento del flujo alrededor de una esfera experimenta cambios dramáticos según el número de Reynold ($Re$), calculado en función de la dimensión típica del sistema ($R$), que en este caso corresponde al radio de la esfera. Además, el número de Reynold ($Re$) es una función de la velocidad media del fluido ($v$), la densidad ($\rho$) y la viscosidad ($\eta$) según:
| $ Re =\displaystyle\frac{ \rho R v }{ \eta }$ |
el número de Reynold ($Re$) expresa la proporción entre la inercia y la viscosidad del sistema. Mientras la viscosidad domina, el flujo se comporta de manera laminar, pero en el caso contrario, domina la inercia. En el primer caso, el medio tiene tiempo de adaptarse, mientras que en el segundo, el flujo no dispone del tiempo suficiente, generando zonas de vórtices o incluso comportamientos caóticos.
El siguiente diagrama resume los diferentes comportamientos:
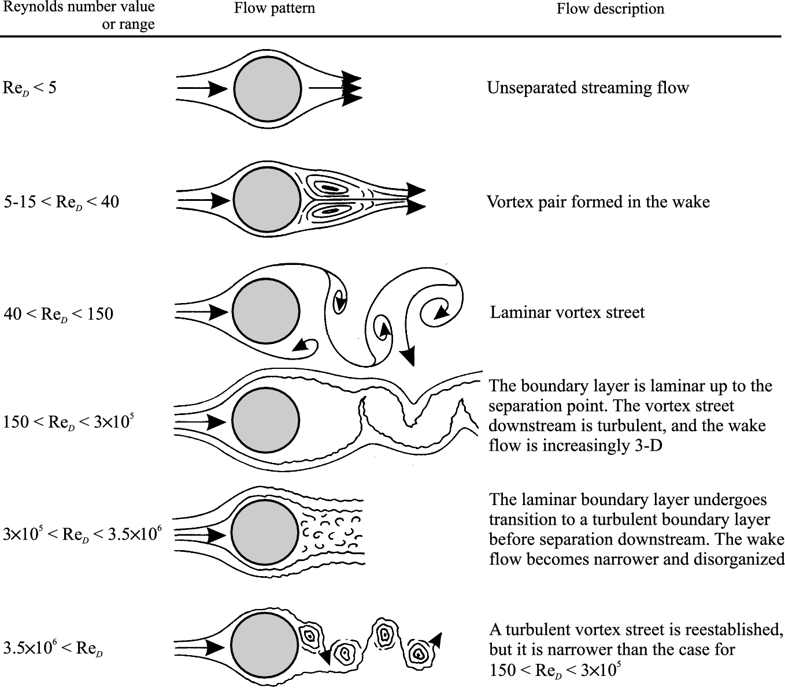
Esquema del tipo de flujo según numero de Reynold (libro Introduction to Transport Phenomena Modeling, Gianpaolo Ruocco - https://link.springer.com/chapter/10.1007/978-3-319-66822-2_3)
ID:(1890, 0)
Esfera en flujo; Re entre 5 y 40
Descripción 
Cuando el número de Reynold ($Re$) está entre 5 y 40, el flujo muestra la formación de dos torbellinos detrás de la esfera:

Flujo en torno a una esfera para numero de Reynold entre 5 y 40 (https://aerospaceengineeringblog.com/how-quickly-do-gas-bubbles-rise-in-a-pint-of-beer/)
ID:(11058, 0)
Esfera en flujo; Re entre 40 y 150
Descripción 
Cuando el número de Reynold ($Re$) está entre 40 y 150, el flujo muestra la formación de torbellinos alternativos, dando lugar a lo que se conoce como una calle de Karman:

Flujo en torno a una esfera para numero de Reynold entre 40 y 150 (https://www.researchgate.net/publication/303369967_Experimental_investigation_of_low_mode_number_cylinders_subjected_to_vortex-induced_vibrations)
ID:(11059, 0)
Esfera en flujo; Re entre 150 y 3E+5
Descripción 
Cuando el número de Reynold ($Re$) se encuentra entre 150 y 3E+5, el flujo muestra un nivel considerable de caos dentro de una estructura macroscópica:
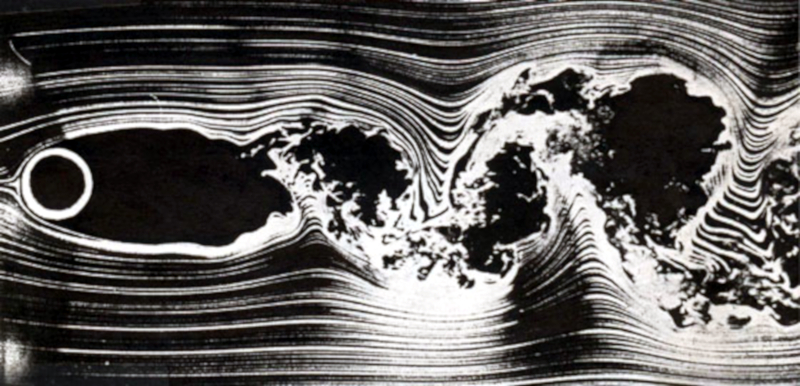
Flujo en torno a una esfera para numero de Reynold entre 150 y 3E+5 ()
ID:(11060, 0)
Esfera en flujo; Re mayor que 3E+5
Descripción 
Cuando el número de Reynold ($Re$) supera los 3E+5, se comienza a formar una zona caótica detrás de la esfera en la que ya no se pueden reconocer torbellinos claramente (o estos tienen dimensiones muy pequeñas).
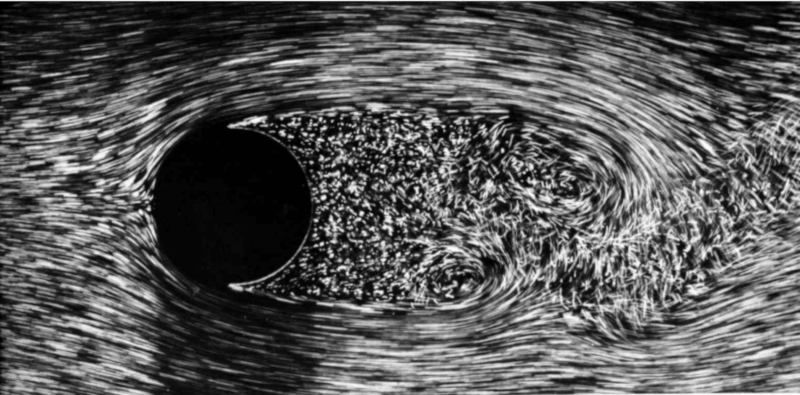
Flujo en torno a una esfera para numero de Reynold mayores de 3E+5 (https://www.pinterest.cl/pin/514888169895997311/)
ID:(11061, 0)
Modelo
Top 
Parámetros
Variables
Cálculos
Cálculos
Cálculos
Ecuaciones
$ C_W = \displaystyle\frac{24}{ Re }(1 + 0.15 Re ^{0.687})$
C_W =24*(1+ Re ^0.687)/ Re
$ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$
F_W = rho * S_p * C_W * v ^2/2
$ Re =\displaystyle\frac{ \rho R v }{ \eta }$
Re = rho * R * v / eta
ID:(15899, 0)
Número de Reynold
Ecuación 
El criterio clave para determinar si un medio es laminar o turbulento es el llamado numero de Reynold que compara la energía asociada a la inercia con aquella asociada a la viscosiadad. La primera depende de la densidad ($\rho$), la velocidad media del fluido ($v$) y la dimensión típica del sistema ($R$) mientras que la segunda de la viscosidad ($\eta$) con lo que se define:
ID:(3177, 0)
Coeficiente de arrastre de una esfera
Ecuación 
Empíricamente, el coeficiente de resistencia ($C_W$) se puede modelar en función de el número de Reynold ($Re$) de la siguiente manera:
ID:(15900, 0)
Fuerza de resistencia
Ecuación 
La fuerza de resistencia ($F_W$) se puede calcular utilizando la densidad ($\rho$), el coeficiente de resistencia ($C_W$), el perfil total del objeto ($S_p$) y la velocidad respecto del medio ($v$) de acuerdo con la siguiente fórmula:
De forma similar a cómo se derivó la ecuación para la fuerza de sustentación ($F_L$) utilizando la densidad ($\rho$), el coeficiente de sustentación ($C_L$), la superficie que genera sustentación ($S_w$) y la velocidad respecto del medio ($v$)
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
en esta analogía, lo que corresponde a la superficie que genera sustentación ($S_w$) será equivalente a el perfil total del objeto ($S_p$) y el coeficiente de sustentación ($C_L$) a el coeficiente de resistencia ($C_W$), con lo que se calcula la fuerza de resistencia ($F_W$):
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
El coeficiente de resistencia se mide y, en flujos turbulentos sobre cuerpos aerodinámicos, generalmente se registran valores alrededor de 0.4.
ID:(4418, 0)
