User:
Moment of inertia
Storyboard 
To maneuver an aircraft, it is necessary to orient it in the desired position to change the flight path and/or altitude. To achieve this, the plane is equipped with ailerons at the wingtips, control surfaces on the rear wings (stabilizers), and a rudder on the tail, which generate forces. These forces, acting at a distance from the center of mass, create torques that allow the aircraft to rotate around its various axes.
The extent of the rotation depends on the moments of inertia, with the fuselage and wings being significant contributors. Therefore, estimating these moments of inertia is essential for predicting the aircraft's response to maneuvers and ensuring precise control during flight.
ID:(2117, 0)
Simplified model of the moment of inertia
Description
It can be assumed that the center of mass of the aircraft is located at the center of the fuselage, at the height of the wings. Therefore, the simplest model to describe its dynamics considers the fuselage as a central cylinder and the wings as thin rectangles.
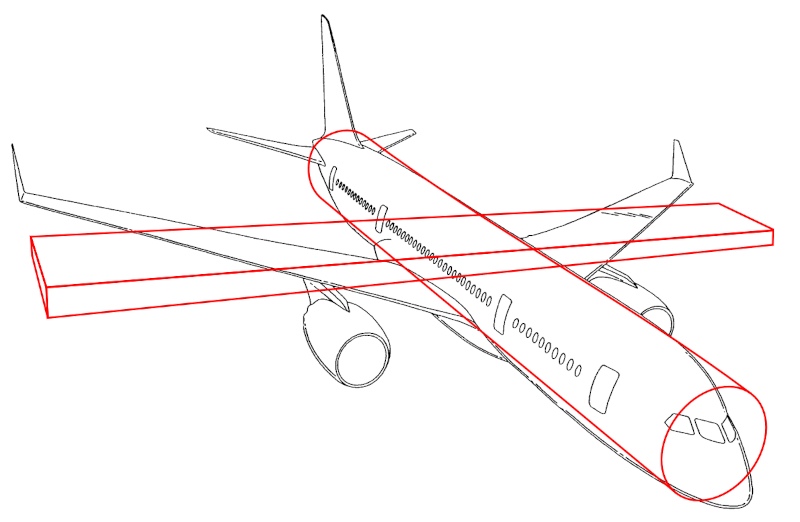
In a first approximation, the moment of inertia of the aircrafts body around its longitudinal axis can be neglected, as the moment of inertia of the wings dominates in the rotations around this axis.
Similarly, in pitching motions, the moment of inertia of the wings relative to their own axis can initially be disregarded since it has a minor effect compared to other forces.
For a more refined model, the contributions of these moments of inertia can be added, along with the three thin rectangles representing the rudder and the two elevators. This would provide a more accurate simulation of the aircrafts dynamics, particularly in more complex maneuvers.
ID:(15983, 0)
Wing mass
Description
The wing mass ($m_w$) can be approximated as the volume of a rectangular parallelepiped multiplied by the density of the aircraft:
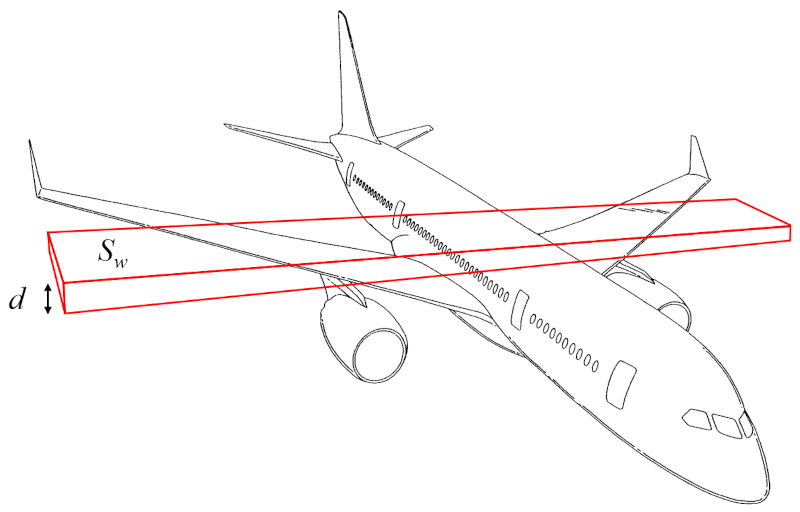
The volume can thus be calculated from the surface that generates lift ($S_w$) and the wing height ($d$).
Therefore, the wing mass ($m_w$) is determined using the aircraft body density ($\rho_a$), the surface that generates lift ($S_w$), and the wing height ($d$), as follows:
| $ m_w = \rho_a S_w d $ |
ID:(15989, 0)
Aircraft body mass
Description
The aircraft body mass ($m_p$) can be approximated as the volume of a cylinder multiplied by the density of the aircraft:
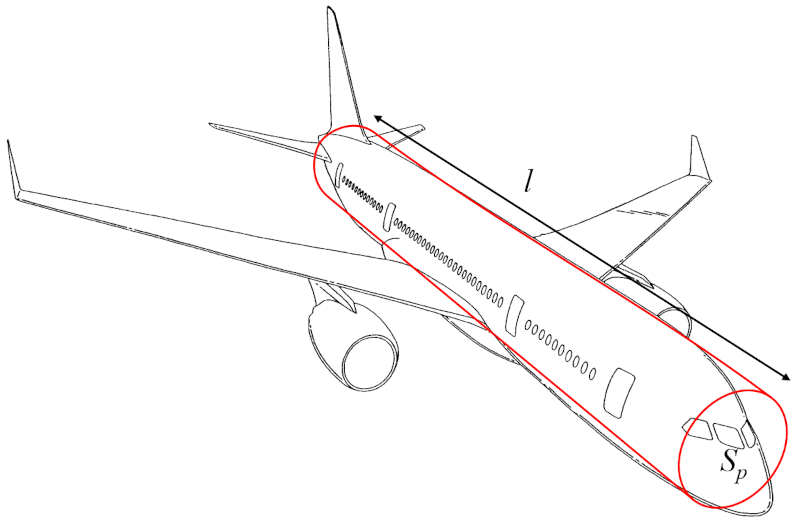
The volume can thus be calculated using the total object profile ($S_p$) (the radius or diameter) and the distance along the wing ($l$) (the height of the cylinder).
Therefore, the aircraft body mass ($m_p$) is determined from the aircraft body density ($\rho_a$), the total object profile ($S_p$), and the distance along the wing ($l$), as follows:
| $ m_p = \rho_a S_p l $ |
ID:(15990, 0)
Moment of inertia for pitching
Description
The wing axis moment of inertia ($I_e$) can be approximated as the moment of inertia of a cylinder representing the body of the aircraft, rotating around an axis perpendicular to the cylinder's axis, which is parallel to the wings:
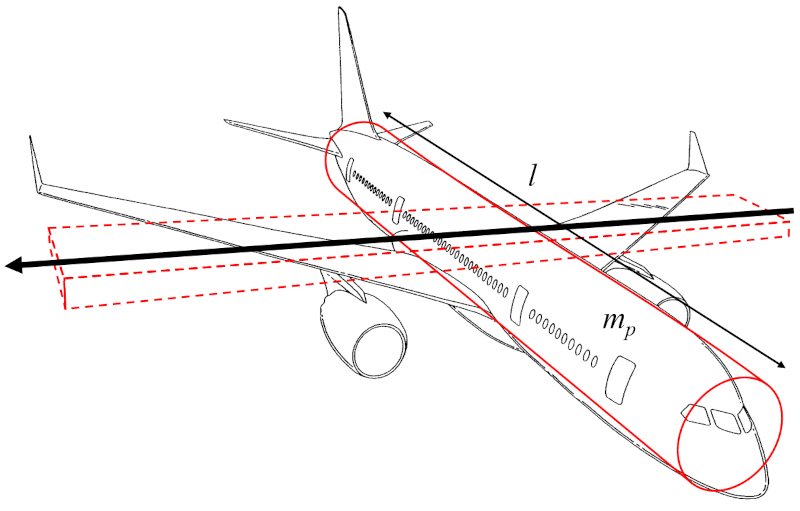
Since the wing width ($w$) is much smaller than the distance along the wing ($l$), the term involving $w^2$ can be neglected, focusing only on the aircraft body mass ($m_p$) and the term with the distance along the wing ($l$) squared.
Therefore, the wing axis moment of inertia ($I_e$) is calculated using the aircraft body mass ($m_p$) and the distance along the wing ($l$) as follows:
 $ I_e = \displaystyle\frac{1}{12} m_p l ^2$ |
ID:(15991, 0)
Moment of inertia for yaw
Description
The vertical axis moment of inertia ($I_r$) can be approximated as the sum of the moment of inertia of a cylinder representing the aircraft fuselage, rotating around an axis perpendicular to its longitudinal axis, and the moment of inertia of a rectangular parallelepiped representing the wings, rotating around an axis perpendicular to them:
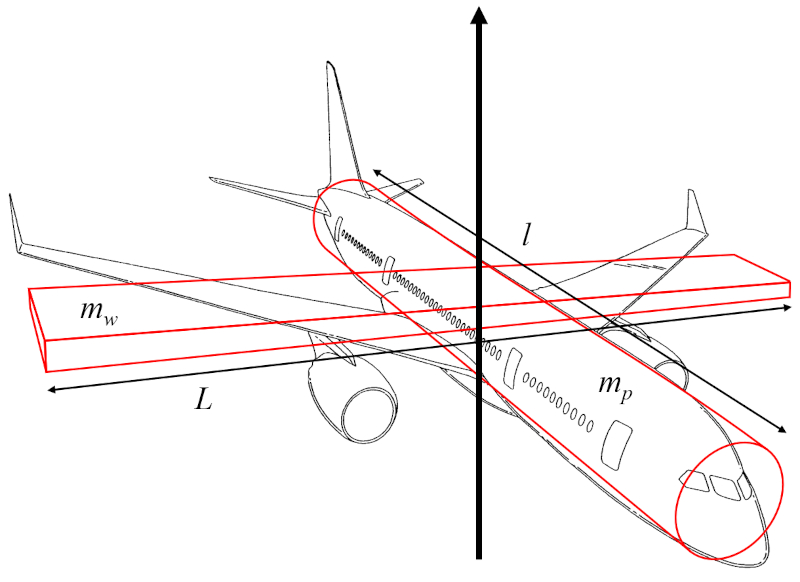
If, for the estimation of the vertical axis moment of inertia ($I_r$), it is assumed that the radius of the fuselage cylinder is much smaller than the distance along the wing ($l$) and the wing width ($w$) is much smaller than the wing span ($L$), the moment of inertia of the cylinder primarily depends on the aircraft body mass ($m_p$) and the distance along the wing ($l$), while the moment of inertia of the parallelepiped depends on the wing mass ($m_w$) and the wing span ($L$).
Therefore, the vertical axis moment of inertia ($I_r$) is calculated using the aircraft body mass ($m_p$), the wing mass ($m_w$), the wing span ($L$), and the distance along the wing ($l$) as follows:
| $ I_r = \displaystyle\frac{1}{12}( m_p l ^2 + m_w L ^2)$ |
ID:(15993, 0)
Moment of inertia for rolling
Description
The moment of inertia axis of the plane ($I_a$) can be approximated as the moment of inertia of a rectangular parallelepiped representing the aircraft's wing, rotating around an axis parallel to its width:
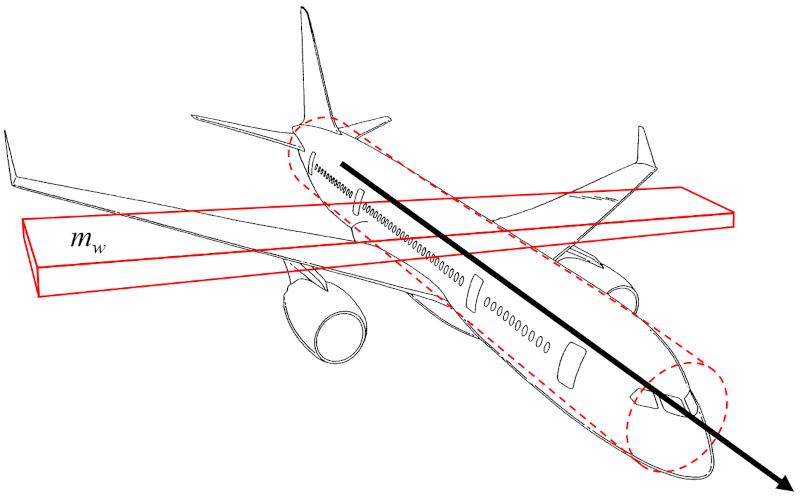
Since the aircraft's body is relatively narrow, the moment of inertia of the cylindrical body can be neglected as a first approximation. As a result, the moment of inertia axis of the plane ($I_a$) is proportional to the wing mass ($m_w$) and the square of the wing span ($L$).
Therefore, the moment of inertia axis of the plane ($I_a$) is calculated using the wing mass ($m_w$) and the wing span ($L$) as follows:
| $ I_a = \displaystyle\frac{1}{6} m_w L ^2$ |
ID:(15992, 0)
Wing mass
Equation
The wing mass ($m_w$) is calculated from the aircraft body density ($\rho_a$), the surface that generates lift ($S_w$), and the wing height ($d$), as follows:
| $ m_w = \rho_a S_w d $ |
ID:(15984, 0)
Aircraft body mass
Equation
The aircraft body mass ($m_p$) is calculated from the aircraft body density ($\rho_a$), the total object profile ($S_p$), and the distance along the wing ($l$), as follows:
| $ m_p = \rho_a S_p l $ |
ID:(15985, 0)
Moment of inertia for pitching
Equation
The wing mass ($m_w$) is calculated from the aircraft body mass ($m_p$) and the distance along the wing ($l$), as follows:
| $ I_e = \displaystyle\frac{1}{12} m_p l ^2$ |
ID:(15987, 0)
Moment of inertia for yaw
Equation
The vertical axis moment of inertia ($I_r$) is calculated from the wing mass ($m_w$), the wing span ($L$) and the distance along the wing ($l$), as follows:
| $ I_r = \displaystyle\frac{1}{12}( m_p l ^2 + m_w L ^2)$ |
ID:(15988, 0)
Moment of inertia for rolling
Equation
The moment of inertia axis of the plane ($I_a$) is calculated from the wing mass ($m_w$) and the wing span ($L$), as follows:
| $ I_a = \displaystyle\frac{1}{6} m_w L ^2$ |
ID:(15986, 0)