Utilisateur:
Moment d'inertie
Storyboard 
Pour manuvrer un avion, il est nécessaire de l'orienter dans la position souhaitée afin de changer de trajectoire et/ou d'altitude. Pour ce faire, l'avion est équipé de ailerons aux extrémités des ailes, de surfaces de contrôle sur les stabilisateurs arrière et d'une gouverne de direction à la queue, qui génèrent des forces. Ces forces, en agissant à une certaine distance du centre de masse, créent des couples qui permettent de faire pivoter l'avion autour de ses différents axes.
L'amplitude de la rotation dépend des moments d'inertie, auxquels le fuselage et les ailes contribuent principalement. Il est donc essentiel d'estimer ces moments d'inertie pour prédire la réponse de l'avion aux manuvres et assurer un contrôle précis pendant le vol.
ID:(2117, 0)
Modèle simplifié du moment d'inertie
Description
On peut supposer que le centre de masse de l'avion est situé au centre du fuselage, à la hauteur des ailes. Ainsi, le modèle le plus simple pour décrire sa dynamique considère le fuselage comme un cylindre central et les ailes comme des rectangles fins.
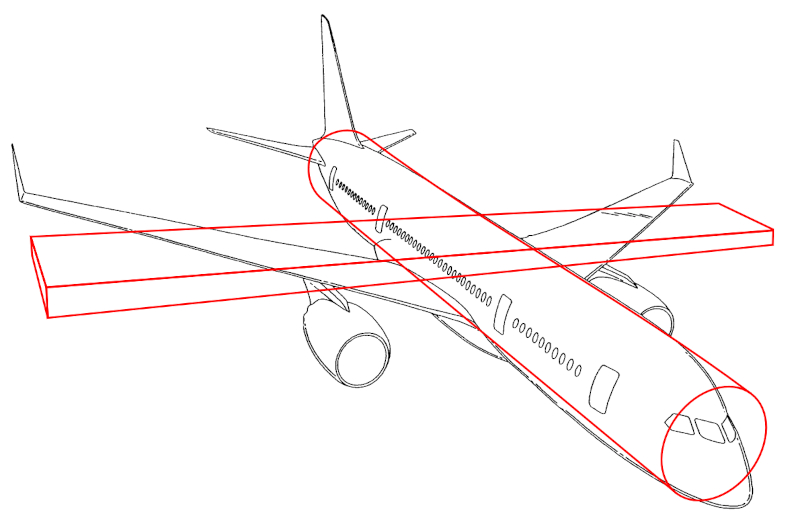
Dans une première approximation, on peut négliger le moment d'inertie du fuselage autour de son axe longitudinal, car le moment d'inertie des ailes domine dans les rotations autour de cet axe.
De même, pour les mouvements de tangage, on peut dans un premier temps ignorer le moment d'inertie des ailes par rapport à leur propre axe, car cet effet est mineur par rapport aux autres forces.
Pour affiner le modèle, on peut ajouter ces contributions des moments d'inertie, ainsi que les trois rectangles fins représentant la gouverne de direction et les deux gouvernes de profondeur. Cela permettrait une simulation plus précise de la dynamique de l'avion, notamment lors de manuvres plus complexes.
ID:(15983, 0)
Masse de l'aile
Description
A masse de l'aile ($m_w$) peut être approximé comme le volume d'un parallélépipède rectangle multiplié par la densité de l'aéronef :
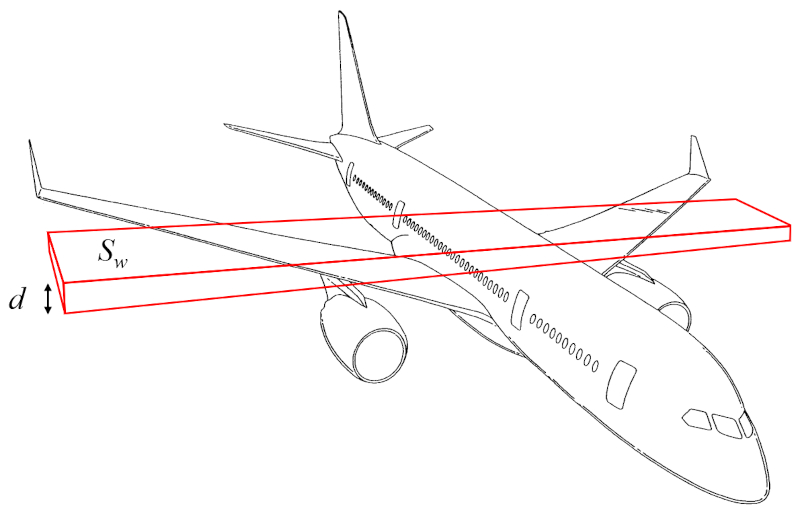
Le volume peut donc être calculé à partir de a surface génératrice de portance ($S_w$) et a hauteur de l'aile ($d$).
Ainsi, a masse de l'aile ($m_w$) est déterminé en utilisant le densité du corps de l'avion ($\rho_a$), a surface génératrice de portance ($S_w$) et a hauteur de l'aile ($d$), de la manière suivante :
| $ m_w = \rho_a S_w d $ |
ID:(15989, 0)
Masse corporelle de l'avion
Description
A masse corporelle de l'avion ($m_p$) peut être approximé comme le volume d'un cylindre multiplié par la densité de l'aéronef :
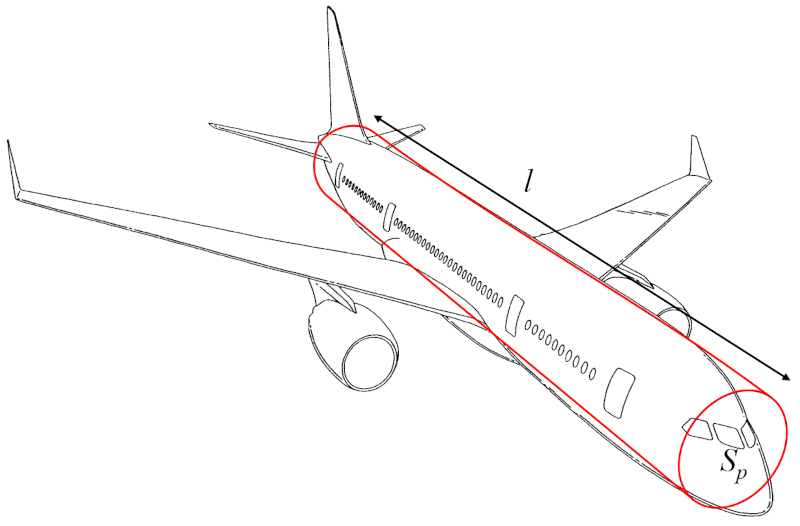
Le volume peut donc être calculé en utilisant le profil total de l'objet ($S_p$) (le rayon ou le diamètre) et le distance le long de l'aile ($l$) (la hauteur du cylindre).
Ainsi, a masse corporelle de l'avion ($m_p$) est déterminé à partir de le densité du corps de l'avion ($\rho_a$), le profil total de l'objet ($S_p$) et le distance le long de l'aile ($l$), de la manière suivante :
| $ m_p = \rho_a S_p l $ |
ID:(15990, 0)
Moment d'inertie pour le tangage
Description
Le moment d'inertie de l'axe de l'aile ($I_e$) peut être approximé comme le moment d'inertie d'un cylindre représentant le corps de l'avion, tournant autour d'un axe perpendiculaire à l'axe du cylindre, parallèle aux ailes :
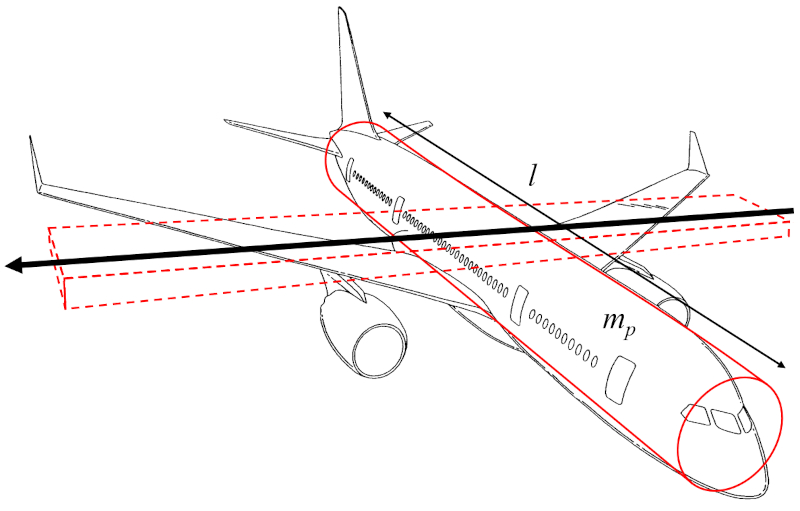
Étant donné que le largeur de l'aile ($w$) est beaucoup plus petit que le distance le long de l'aile ($l$), le terme impliquant $w^2$ peut être négligé, et l'on se concentre uniquement sur a masse corporelle de l'avion ($m_p$) et le terme le distance le long de l'aile ($l$) au carré.
Par conséquent, le moment d'inertie de l'axe de l'aile ($I_e$) se calcule à partir de a masse corporelle de l'avion ($m_p$) et le distance le long de l'aile ($l$), comme suit :
 $ I_e = \displaystyle\frac{1}{12} m_p l ^2$ |
ID:(15991, 0)
Moment d'inertie pour le lacet
Description
Le moment d'inertie de l'axe vertical ($I_r$) peut être approximé comme la somme du moment d'inertie d'un cylindre représentant le fuselage de l'avion, tournant autour d'un axe perpendiculaire à son axe longitudinal, et du moment d'inertie d'un parallélépipède rectangle représentant les ailes, tournant autour d'un axe perpendiculaire à celles-ci :
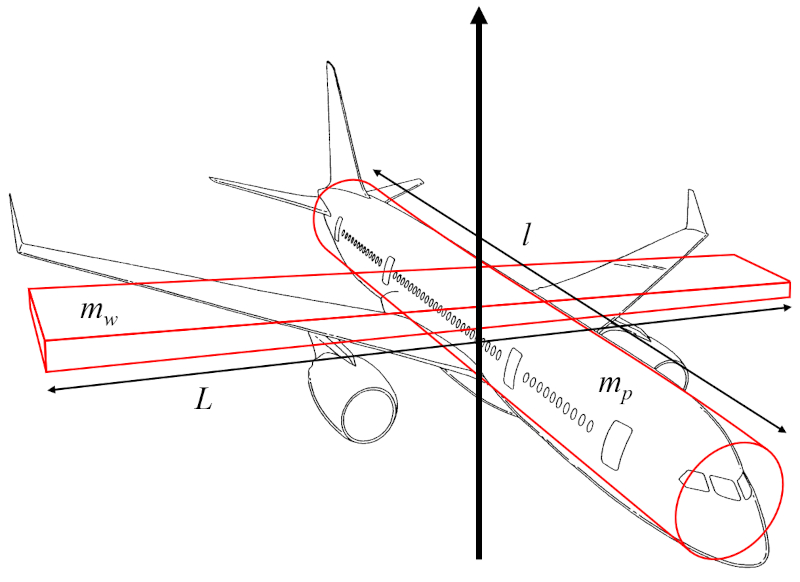
Si, pour l'estimation de le moment d'inertie de l'axe vertical ($I_r$), on suppose que le rayon du cylindre du fuselage est bien inférieur à Le distance le long de l'aile ($l$) et que le largeur de l'aile ($w$) est beaucoup plus petit que a envergure des ailes ($L$), le moment d'inertie du cylindre dépend principalement de a masse corporelle de l'avion ($m_p$) et le distance le long de l'aile ($l$), tandis que le moment d'inertie du parallélépipède dépend de a masse de l'aile ($m_w$) et a envergure des ailes ($L$).
Ainsi, le moment d'inertie de l'axe vertical ($I_r$) est calculé à partir de a masse corporelle de l'avion ($m_p$), a masse de l'aile ($m_w$), ($$)6337 ($$)10333
| $ I_r = \displaystyle\frac{1}{12}( m_p l ^2 + m_w L ^2)$ |
ID:(15993, 0)
Moment d'inertie pour rouler
Description
Le moment d'inertie de l'axe de l'avion ($I_a$) peut être approximé comme le moment d'inertie d'un parallélépipède rectangle représentant l'aile de l'avion, tournant autour d'un axe parallèle à sa largeur :
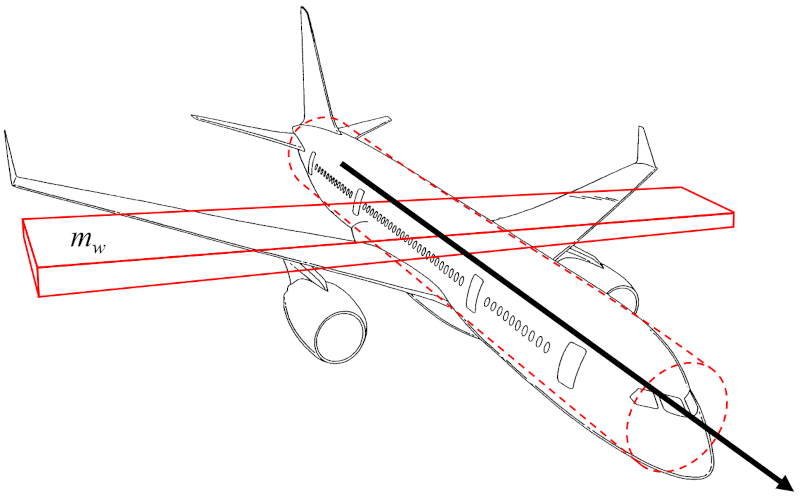
Étant donné que le fuselage de l'avion est relativement étroit, le moment d'inertie du cylindre qui le représente peut être négligé dans une première approximation. Par conséquent, le moment d'inertie de l'axe de l'avion ($I_a$) est proportionnel à A masse de l'aile ($m_w$) et au carré de a envergure des ailes ($L$).
Ainsi, le moment d'inertie de l'axe de l'avion ($I_a$) est calculé à partir de a masse de l'aile ($m_w$) et ($$)6337
| $ I_a = \displaystyle\frac{1}{6} m_w L ^2$ |
ID:(15992, 0)
Masse de l'aile
Équation
A masse de l'aile ($m_w$) est calculé à partir de le densité du corps de l'avion ($\rho_a$), a surface génératrice de portance ($S_w$) et a hauteur de l'aile ($d$), comme suit :
| $ m_w = \rho_a S_w d $ |
ID:(15984, 0)
Masse corporelle de l'avion
Équation
A masse corporelle de l'avion ($m_p$) est calculé à partir de le densité du corps de l'avion ($\rho_a$), le profil total de l'objet ($S_p$) et le distance le long de l'aile ($l$), comme suit :
| $ m_p = \rho_a S_p l $ |
ID:(15985, 0)
Moment d'inertie pour le tangage
Équation
A masse de l'aile ($m_w$) est calculé à partir de a masse corporelle de l'avion ($m_p$) et ($$)10333
| $ I_e = \displaystyle\frac{1}{12} m_p l ^2$ |
ID:(15987, 0)
Moment d'inertie pour le lacet
Équation
Le moment d'inertie de l'axe vertical ($I_r$) est calculé à partir de a masse de l'aile ($m_w$), a envergure des ailes ($L$) et ($$)10333
| $ I_r = \displaystyle\frac{1}{12}( m_p l ^2 + m_w L ^2)$ |
ID:(15988, 0)
Moment d'inertie pour rouler
Équation
Le moment d'inertie de l'axe de l'avion ($I_a$) est calculé à partir de a masse de l'aile ($m_w$) et ($$)6337
| $ I_a = \displaystyle\frac{1}{6} m_w L ^2$ |
ID:(15986, 0)