Usuario:
Momento de inercia
Storyboard 
Para maniobrar un avión, es necesario orientarlo en la dirección adecuada para cambiar la ruta y/o la altitud de vuelo. Para lograr esto, el avión está equipado con alerones en los extremos de las alas, superficies de control en las alas traseras (estabilizadores), y un timón en la cola, que generan fuerzas. Estas fuerzas, al actuar a cierta distancia del centro de masa, producen torques que permiten rotar el avión en sus diferentes ejes.
La magnitud de la rotación dependerá de los momentos de inercia, en los que tanto el cuerpo de la aeronave como las alas juegan un papel crucial. Por lo tanto, es fundamental estimar estos momentos de inercia para predecir cómo responderá el avión a las maniobras y garantizar un control preciso durante el vuelo.
ID:(2117, 0)
Modelo simplificado del momento de inercia
Descripción
Se puede asumir que el centro de masa de la aeronave se encuentra en el centro del fuselaje, a la altura de las alas. Por lo tanto, el modelo más simple para describir su dinámica es considerar el fuselaje como un cilindro central y las alas como rectángulos delgados.
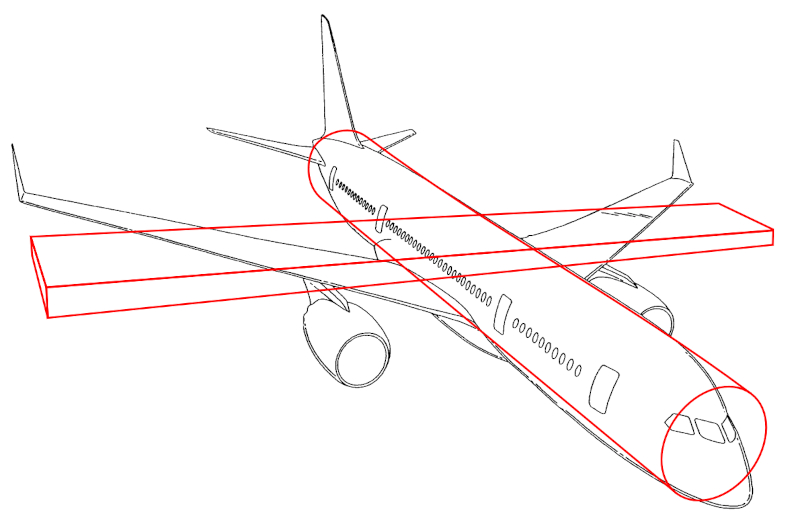
En una primera aproximación, se puede despreciar el momento de inercia del cuerpo del avión en torno a su eje longitudinal, ya que el momento de inercia de las alas predomina en las rotaciones alrededor de dicho eje.
De igual manera, en los movimientos de cabeceo, se puede ignorar inicialmente el momento de inercia de las alas respecto a su propio eje, dado que este tiene un efecto menor en comparación con otras fuerzas.
Para un modelo más detallado, se podrían agregar las contribuciones adicionales de estos momentos de inercia junto con los tres rectángulos delgados que representan el timón y los dos elevadores. Esto permitiría una simulación más precisa de la dinámica de vuelo de la aeronave, especialmente en maniobras más complejas.
ID:(15983, 0)
Masa de las alas
Descripción
La masa de las alas ($m_w$) se puede aproximar como el volumen de un paralelepípedo recto multiplicado por la densidad de la aeronave:
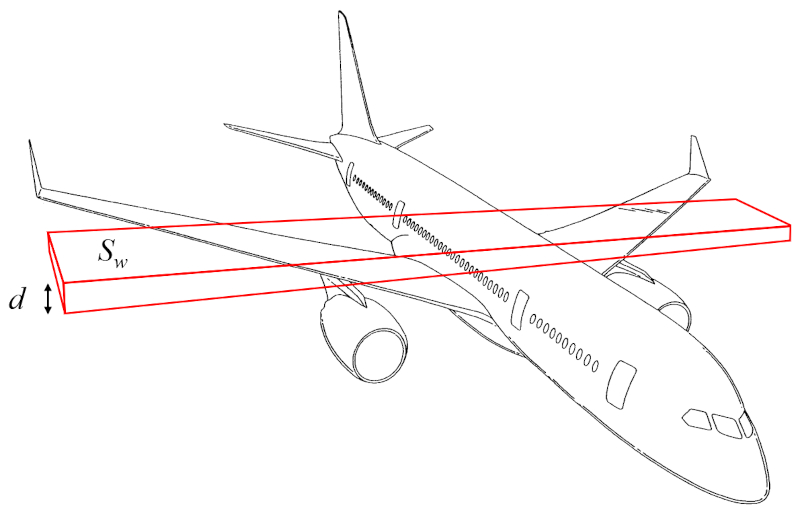
El volumen, por lo tanto, se puede calcular a partir de la superficie que genera sustentación ($S_w$) y la altura del ala ($d$).
Por ello, la masa de las alas ($m_w$) se determina utilizando el densidad del cuerpo de la aeronave ($\rho_a$), la superficie que genera sustentación ($S_w$), y la altura del ala ($d$), de la siguiente manera:
| $ m_w = \rho_a S_w d $ |
ID:(15989, 0)
Masa del cuerpo de la aeronave
Descripción
La masa del cuerpo de la aeronave ($m_p$) se puede aproximar como el volumen de un cilindro multiplicado por la densidad de la aeronave:
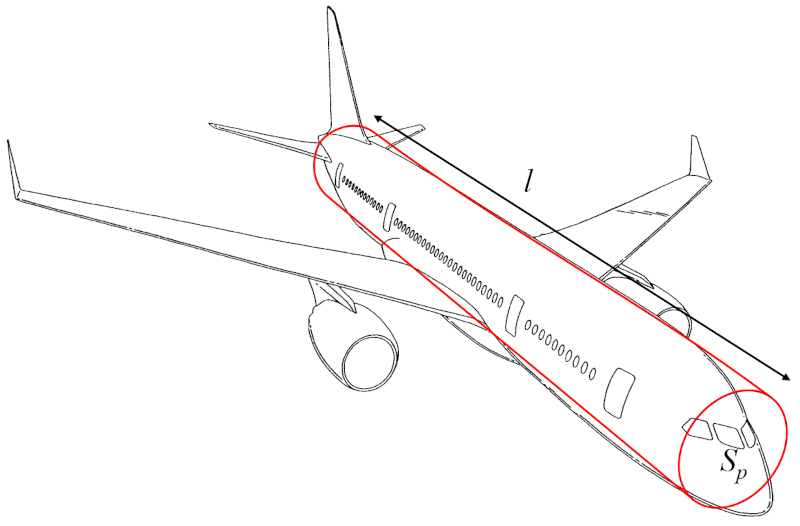
El volumen, por lo tanto, se puede calcular utilizando el perfil total del objeto ($S_p$) (el radio o diámetro) y el distancia a lo largo del ala ($l$) (la altura del cilindro).
Por lo tanto, la masa del cuerpo de la aeronave ($m_p$) se determina a partir de el densidad del cuerpo de la aeronave ($\rho_a$), el perfil total del objeto ($S_p$) y el distancia a lo largo del ala ($l$), de la siguiente manera:
| $ m_p = \rho_a S_p l $ |
ID:(15990, 0)
Momento de inercia para cabeceo
Descripción
El momento de inercia eje del ala ($I_e$) puede aproximarse como el momento de inercia de un cilindro que representa el fuselaje de la aeronave, rotando alrededor de un eje perpendicular al eje longitudinal del cilindro, paralelo a las alas:
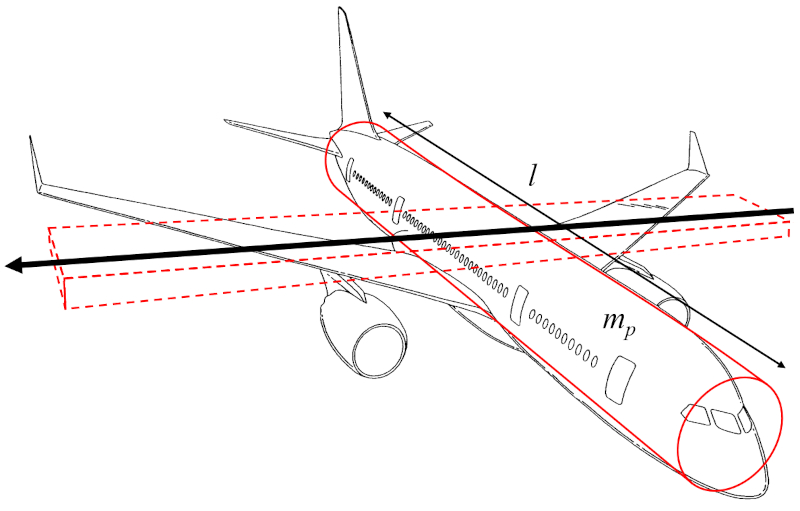
Dado que el ancho del ala ($w$) es significativamente menor que el distancia a lo largo del ala ($l$), se puede despreciar el término que involucra $w^2$, y trabajar únicamente con la masa del cuerpo de la aeronave ($m_p$) y el término el distancia a lo largo del ala ($l$) al cuadrado.
Por lo tanto, el momento de inercia eje del ala ($I_e$) se calcula a partir de la masa del cuerpo de la aeronave ($m_p$) y el distancia a lo largo del ala ($l$), de la siguiente manera:
 $ I_e = \displaystyle\frac{1}{12} m_p l ^2$ |
ID:(15991, 0)
Momento de inercia para guiñado
Descripción
El momento de inercia eje vertical ($I_r$) puede aproximarse como la suma del momento de inercia de un cilindro que representa el fuselaje de la aeronave, rotando alrededor de un eje perpendicular a su eje longitudinal, y el momento de inercia de un paralelepípedo que representa las alas, rotando en torno a un eje perpendicular a ellas:
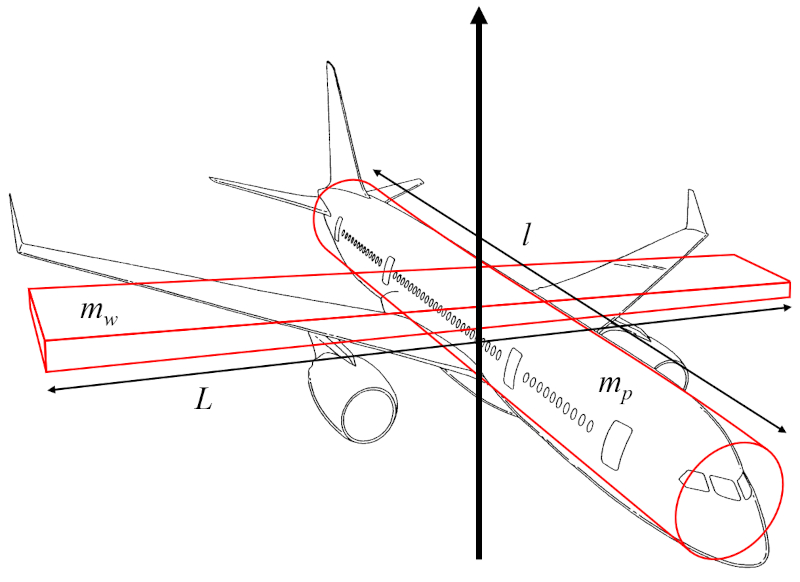
Si para la estimación de el momento de inercia eje vertical ($I_r$) se asume que el radio del cilindro del fuselaje es mucho menor que el distancia a lo largo del ala ($l$) y que el ancho del ala ($w$) es mucho menor que la envergadura de las alas ($L$), entonces el momento de inercia del cilindro depende principalmente de la masa del cuerpo de la aeronave ($m_p$) y el distancia a lo largo del ala ($l$), mientras que el del paralelepípedo depende de la masa de las alas ($m_w$) y la envergadura de las alas ($L$).
Por lo tanto, el momento de inercia eje vertical ($I_r$) se calcula a partir de la masa del cuerpo de la aeronave ($m_p$), la masa de las alas ($m_w$), la envergadura de las alas ($L$), y el distancia a lo largo del ala ($l$), de la siguiente manera:
| $ I_r = \displaystyle\frac{1}{12}( m_p l ^2 + m_w L ^2)$ |
ID:(15993, 0)
Momento de inercia para rodar
Descripción
El momento de inercia eje del avión ($I_a$) puede aproximarse como el momento de inercia de un paralelepípedo recto que representa el ala de la aeronave, rotando alrededor de un eje paralelo a su ancho:
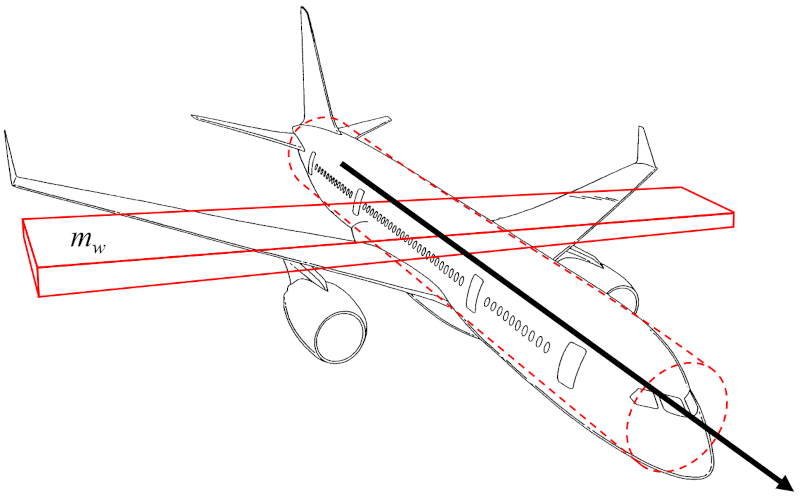
Dado que el cuerpo de la aeronave es relativamente estrecho, se puede, en una primera aproximación, despreciar el momento de inercia del cilindro que lo representa. De esta forma, el momento de inercia eje del avión ($I_a$) resulta proporcional a la masa de las alas ($m_w$) y al cuadrado de la envergadura de las alas ($L$).
Por lo tanto, el momento de inercia eje del avión ($I_a$) se calcula a partir de la masa de las alas ($m_w$) y la envergadura de las alas ($L$), de la siguiente manera:
| $ I_a = \displaystyle\frac{1}{6} m_w L ^2$ |
ID:(15992, 0)
Masa de las alas
Ecuación
La masa de las alas ($m_w$) se calcula a partir de el densidad del cuerpo de la aeronave ($\rho_a$), la superficie que genera sustentación ($S_w$) y la altura del ala ($d$), de la siguiente manera:
| $ m_w = \rho_a S_w d $ |
ID:(15984, 0)
Masa del cuerpo de la aeronave
Ecuación
La masa del cuerpo de la aeronave ($m_p$) se calcula a partir de el densidad del cuerpo de la aeronave ($\rho_a$), el perfil total del objeto ($S_p$) y el distancia a lo largo del ala ($l$), de la siguiente manera:
| $ m_p = \rho_a S_p l $ |
ID:(15985, 0)
Momento de inercia para cabeceo
Ecuación
El momento de inercia eje del ala ($I_e$) se calcula a partir de la masa del cuerpo de la aeronave ($m_p$) y el distancia a lo largo del ala ($l$), de la siguiente manera:
| $ I_e = \displaystyle\frac{1}{12} m_p l ^2$ |
ID:(15987, 0)
Momento de inercia para guiñado
Ecuación
El momento de inercia eje vertical ($I_r$) se calcula a partir de la masa del cuerpo de la aeronave ($m_p$), la masa de las alas ($m_w$), la envergadura de las alas ($L$) y el distancia a lo largo del ala ($l$), de la siguiente manera:
| $ I_r = \displaystyle\frac{1}{12}( m_p l ^2 + m_w L ^2)$ |
ID:(15988, 0)
Momento de inercia para rodar
Ecuación
El momento de inercia eje del avión ($I_a$) se calcula a partir de la masa de las alas ($m_w$) y la envergadura de las alas ($L$), de la siguiente manera:
| $ I_a = \displaystyle\frac{1}{6} m_w L ^2$ |
ID:(15986, 0)