Benützer:
Trägheitsmoment
Storyboard 
Um ein Flugzeug zu manövrieren, muss es in die gewünschte Position gedreht werden, um die Flugroute und/oder die Flughöhe zu ändern. Dazu ist das Flugzeug mit Querrudern an den Flügelspitzen, Steuerflächen an den Hinterflügeln (Stabilisatoren) und einem Seitenruder am Heck ausgestattet, die Kräfte erzeugen. Diese Kräfte wirken in einem Abstand zum Schwerpunkt und erzeugen Drehmomente, die es ermöglichen, das Flugzeug um seine verschiedenen Achsen zu drehen.
Das Ausmaß der Rotation hängt von den Trägheitsmomenten ab, wobei der Rumpf und die Flügel eine wesentliche Rolle spielen. Daher ist es wichtig, diese Trägheitsmomente abzuschätzen, um die Reaktion des Flugzeugs auf Manöver vorherzusagen und eine präzise Steuerung während des Flugs zu gewährleisten.
ID:(2117, 0)
Vereinfachtes Trägheitsmomentmodell
Beschreibung
Man kann annehmen, dass der Schwerpunkt des Flugzeugs im Zentrum des Rumpfes, auf der Höhe der Flügel, liegt. Daher besteht das einfachste Modell zur Beschreibung seiner Dynamik darin, den Rumpf als Zentralzylinder und die Flügel als dünne Rechtecke zu betrachten.
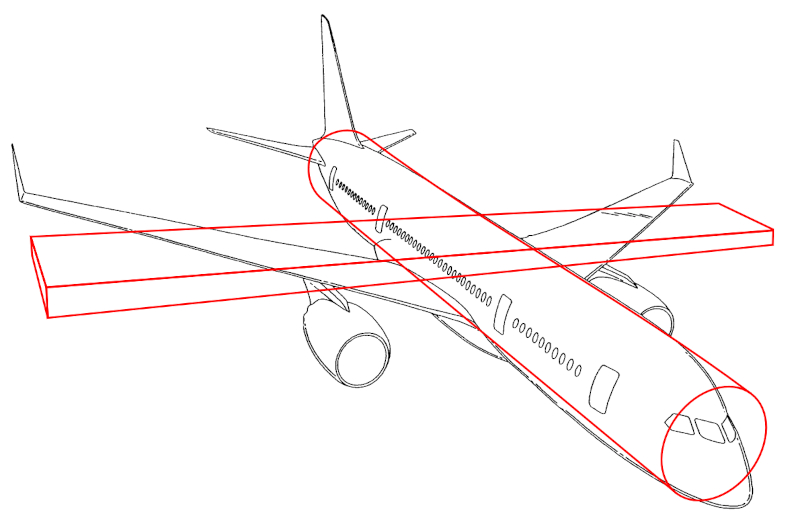
In einer ersten Näherung kann der Trägheitsmoment des Flugzeugrumpfes um seine Längsachse vernachlässigt werden, da der Trägheitsmoment der Flügel bei den Drehungen um diese Achse dominiert.
Ebenso kann man bei Nickbewegungen zunächst den Trägheitsmoment der Flügel um ihre eigene Achse außer Acht lassen, da dieser im Vergleich zu anderen Kräften einen geringeren Einfluss hat.
Um das Modell zu verfeinern, können die Beiträge dieser Trägheitsmomente sowie die drei dünnen Rechtecke, die das Seitenruder und die beiden Höhenruder darstellen, hinzugefügt werden. Dies würde eine genauere Simulation der Flugzeugdynamik ermöglichen, insbesondere bei komplexeren Manövern.
ID:(15983, 0)
Flügelmasse
Beschreibung
Die Flügelmasse ($m_w$) kann als das Volumen eines rechtwinkligen Parallelepipeds multipliziert mit der Dichte des Flugzeugs approximiert werden:
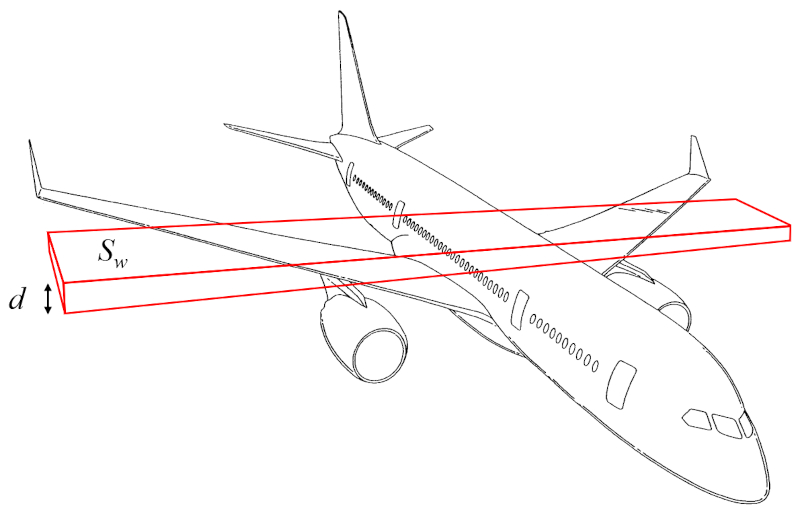
Das Volumen kann somit aus die Oberfläche, die Auftrieb erzeugt ($S_w$) und die Flügelhöhe ($d$) berechnet werden.
Daher wird die Flügelmasse ($m_w$) unter Verwendung von der Dichte des Flugzeugkörpers ($\rho_a$), die Oberfläche, die Auftrieb erzeugt ($S_w$) und die Flügelhöhe ($d$) wie folgt bestimmt:
| $ m_w = \rho_a S_w d $ |
ID:(15989, 0)
Flugzeugkörpermasse
Beschreibung
Die Flugzeugkörpermasse ($m_p$) kann als das Volumen eines Zylinders multipliziert mit der Dichte des Flugzeugs approximiert werden:
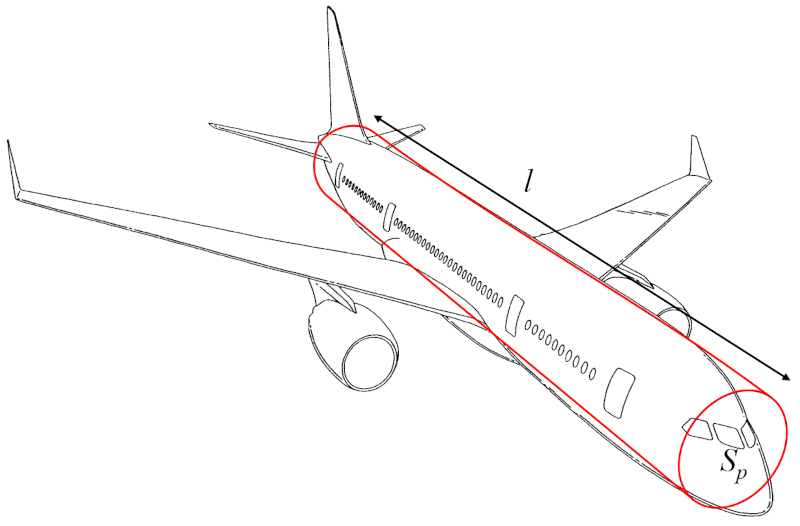
Das Volumen kann daher unter Verwendung von der Gesamtobjektprofil ($S_p$) (dem Radius oder Durchmesser) und der Abstand entlang des Flügels ($l$) (der Höhe des Zylinders) berechnet werden.
Daher wird die Flugzeugkörpermasse ($m_p$) aus der Dichte des Flugzeugkörpers ($\rho_a$), der Gesamtobjektprofil ($S_p$) und der Abstand entlang des Flügels ($l$) wie folgt bestimmt:
| $ m_p = \rho_a S_p l $ |
ID:(15990, 0)
Trägheitsmoment beim Nicken
Beschreibung
Der Trägheitsmoment der Flügelachse ($I_e$) kann als das Trägheitsmoment eines Zylinders approximiert werden, der den Rumpf des Flugzeugs darstellt und sich um eine Achse dreht, die senkrecht zur Achse des Zylinders und parallel zu den Flügeln verläuft:
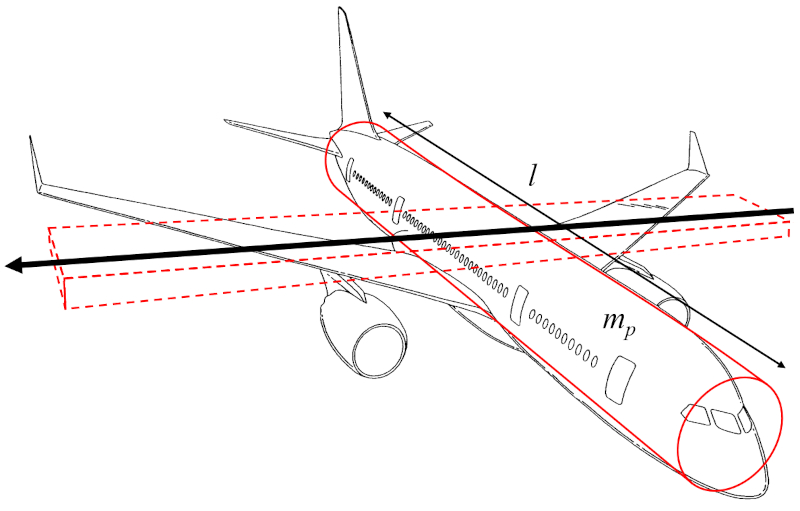
Da der Flügelbreite ($w$) deutlich kleiner ist als der Abstand entlang des Flügels ($l$), kann der Term mit $w^2$ vernachlässigt werden, und es wird nur mit die Flugzeugkörpermasse ($m_p$) und dem Quadrat von der Abstand entlang des Flügels ($l$) gearbeitet.
Daher wird der Trägheitsmoment der Flügelachse ($I_e$) wie folgt aus die Flugzeugkörpermasse ($m_p$) und der Abstand entlang des Flügels ($l$) berechnet:
 $ I_e = \displaystyle\frac{1}{12} m_p l ^2$ |
ID:(15991, 0)
Trägheitsmoment für Gier
Beschreibung
Der Trägheitsmoment der vertikalen Achse ($I_r$) kann als die Summe des Trägheitsmoments eines Zylinders, der den Rumpf des Flugzeugs darstellt und sich um eine Achse dreht, die senkrecht zur Längsachse des Zylinders verläuft, sowie des Trägheitsmoments eines rechtwinkligen Parallelepipeds, das die Flügel darstellt und sich um eine Achse dreht, die senkrecht dazu verläuft, angenähert werden:
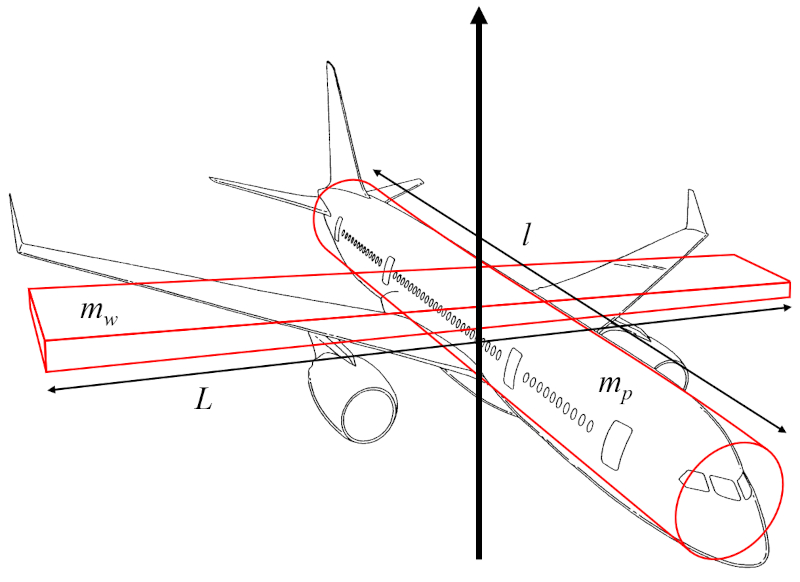
Wenn man bei der Schätzung von der Trägheitsmoment der vertikalen Achse ($I_r$) davon ausgeht, dass der Radius des Zylinders des Rumpfes viel kleiner ist als der Abstand entlang des Flügels ($l$) und der Flügelbreite ($w$) viel kleiner ist als die Spannweite der Flügel ($L$), hängt das Trägheitsmoment des Zylinders hauptsächlich von die Flugzeugkörpermasse ($m_p$) und der Abstand entlang des Flügels ($l$) ab, während das Trägheitsmoment des Parallelepipeds von die Flügelmasse ($m_w$) und die Spannweite der Flügel ($L$) abhängt.
Daher wird der Trägheitsmoment der vertikalen Achse ($I_r$) wie folgt aus die Flugzeugkörpermasse ($m_p$), die Flügelmasse ($m_w$), ($$)6337 ($$)10333
| $ I_r = \displaystyle\frac{1}{12}( m_p l ^2 + m_w L ^2)$ |
ID:(15993, 0)
Trägheitsmoment beim Rollen
Beschreibung
Der Trägheitsmoment der Achse der Ebene ($I_a$) kann als das Trägheitsmoment eines rechtwinkligen Parallelepipeds angenähert werden, das den Flügel des Flugzeugs darstellt und sich um eine Achse dreht, die parallel zur Flügelbreite verläuft:
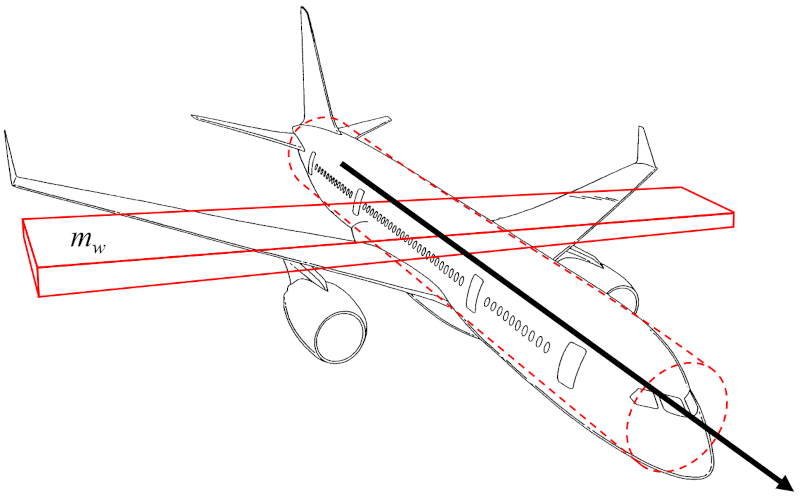
Da der Rumpf des Flugzeugs relativ schmal ist, kann in einer ersten Näherung das Trägheitsmoment des Zylinders, der ihn darstellt, vernachlässigt werden. Somit ist der Trägheitsmoment der Achse der Ebene ($I_a$) proportional zu die Flügelmasse ($m_w$) und dem Quadrat von die Spannweite der Flügel ($L$).
Daher wird der Trägheitsmoment der Achse der Ebene ($I_a$) wie folgt aus die Flügelmasse ($m_w$) und die Spannweite der Flügel ($L$) berechnet:
| $ I_a = \displaystyle\frac{1}{6} m_w L ^2$ |
ID:(15992, 0)
Flügelmasse
Gleichung
Die Flügelmasse ($m_w$) wird aus der Dichte des Flugzeugkörpers ($\rho_a$), die Oberfläche, die Auftrieb erzeugt ($S_w$) und die Flügelhöhe ($d$) berechnet, wie folgt:
| $ m_w = \rho_a S_w d $ |
ID:(15984, 0)
Flugzeugkörpermasse
Gleichung
Die Flugzeugkörpermasse ($m_p$) wird aus der Dichte des Flugzeugkörpers ($\rho_a$), der Gesamtobjektprofil ($S_p$) und der Abstand entlang des Flügels ($l$) berechnet, wie folgt:
| $ m_p = \rho_a S_p l $ |
ID:(15985, 0)
Trägheitsmoment beim Nicken
Gleichung
Die Flügelmasse ($m_w$) wird aus die Flugzeugkörpermasse ($m_p$) und der Abstand entlang des Flügels ($l$) berechnet, wie folgt:
| $ I_e = \displaystyle\frac{1}{12} m_p l ^2$ |
ID:(15987, 0)
Trägheitsmoment für Gier
Gleichung
Der Trägheitsmoment der vertikalen Achse ($I_r$) wird aus die Flügelmasse ($m_w$), die Spannweite der Flügel ($L$) und der Abstand entlang des Flügels ($l$) berechnet, wie folgt:
| $ I_r = \displaystyle\frac{1}{12}( m_p l ^2 + m_w L ^2)$ |
ID:(15988, 0)
Trägheitsmoment beim Rollen
Gleichung
Der Trägheitsmoment der Achse der Ebene ($I_a$) wird aus die Flügelmasse ($m_w$) und die Spannweite der Flügel ($L$) berechnet, wie folgt:
| $ I_a = \displaystyle\frac{1}{6} m_w L ^2$ |
ID:(15986, 0)