Segeln
Storyboard 
Wenn das Objekt (Flugzeug / Vogel) einen leicht negativen Anstellwinkel beibehält, kann ein Teil der Auftriebskraft durch Gegenwirkung zum Boosten beitragen. Im Durchschnitt ist der verbleibende Auftrieb nicht viel geringer als die Schwerkraft, das Objekt wird lange in der Luft gehalten. Sie können von einem extrem langsamen kontrollierten Abstieg oder Gleiten sprechen.
ID:(466, 0)
Segeln
Storyboard 
Wenn das Objekt (Flugzeug / Vogel) einen leicht negativen Anstellwinkel beibehält, kann ein Teil der Auftriebskraft durch Gegenwirkung zum Boosten beitragen. Im Durchschnitt ist der verbleibende Auftrieb nicht viel geringer als die Schwerkraft, das Objekt wird lange in der Luft gehalten. Sie können von einem extrem langsamen kontrollierten Abstieg oder Gleiten sprechen.
Variablen
Berechnungen
Berechnungen
Gleichungen
Die Auftriebskraft ($F_L$), zusammen mit die Spannweite der Flügel ($L$), die Dichte ($\rho$), der Flügel-Höchstgeschwindigkeitsfaktor ($c_t$), der Flügelbodengeschwindigkeitsfaktor ($c_b$), die Obere Flügellänge ($l_t$), die Länge des unteren Flügels ($l_b$) und die Geschwindigkeit in Bezug auf das Medium ($v$), findet sich in
Wenn wir die Oberfläche, die Auftrieb erzeugt ($S_w$) betrachten, gegeben durch die Spannweite der Flügel ($L$), die Obere Flügellänge ($l_t$) und die Länge des unteren Flügels ($l_b$),
und f r der Koeffizient Fahrstuhl ($C_L$), definiert als
erhalten wir
hnlich wie die Gleichung f r die Auftriebskraft ($F_L$) unter Verwendung von die Dichte ($\rho$), der Koeffizient Fahrstuhl ($C_L$), die Oberfläche, die Auftrieb erzeugt ($S_w$) und die Geschwindigkeit in Bezug auf das Medium ($v$) abgeleitet wurde
entspricht in dieser Analogie das, was die Oberfläche, die Auftrieb erzeugt ($S_w$) entspricht, der Gesamtobjektprofil ($S_p$) und der Koeffizient Fahrstuhl ($C_L$) entspricht der Widerstandskoeffizient ($C_W$), woraus die Widerstandskraft ($F_W$) berechnet wird:
Der Widerstandsbeiwert wird gemessen und bei turbulenten Str mungen ber aerodynamischen K rpern werden blicherweise Werte um 0,4 ermittelt.
Wenn wir die Auftriebskraft ($F_L$), die Widerstandskraft ($F_W$), die Körpermasse ($m$), die Gravitationsbeschleunigung ($g$) und der Gleitwinkel ($\phi$) in Betracht ziehen, ist die Kraft beim Gleiten in vertikaler Richtung:
und in horizontaler Richtung:
Dadurch k nnen wir die Widerstandskraft ($F_W$) eliminieren, was zu folgendem f hrt:
$F_L=F_W\displaystyle\frac{\cos\phi}{\sin\phi} \rightarrow F_W(\sin^2\phi+\cos^2\phi)=mg\sin\phi$
Daher ist die Auftriebskraft ($F_L$):
Wenn wir die Auftriebskraft ($F_L$), die Widerstandskraft ($F_W$), die Körpermasse ($m$), die Gravitationsbeschleunigung ($g$) und der Gleitwinkel ($\phi$) in Betracht ziehen, ist die Kraft beim Gleiten in vertikaler Richtung:
und in horizontaler Richtung:
Dadurch k nnen wir die Auftriebskraft ($F_L$) eliminieren, was zu folgendem f hrt:
$F_L=F_W\displaystyle\frac{\cos\phi}{\sin\phi} \rightarrow F_W(\sin^2\phi+\cos^2\phi)=mg\sin\phi$
die Widerstandskraft ($F_W$) sollte sein:
Betrachten wir die Auftriebskraft ($F_L$), die Widerstandskraft ($F_W$), die Körpermasse ($m$), die Gravitationsbeschleunigung ($g$) und der Gleitwinkel ($\phi$). Mit diesen Kr ften wird die Auftriebskraft wie folgt berechnet:
und die Widerstandskraft wie folgt:
Wir k nnen der Gleitwinkel ($\phi$) bestimmen, indem wir die Auftriebskraft ($F_L$) durch die Widerstandskraft ($F_W$) teilen, was zu folgendem Ergebnis f hrt:
$\tan\phi=\displaystyle\frac{F_W}{F_L}$
Dabei wird die Widerstandskraft ($F_W$) mit folgender Gleichung berechnet:
unter Verwendung von der Gesamtobjektprofil ($S_p$) und der Widerstandskoeffizient ($C_W$). Ebenso wird die Auftriebskraft ($F_L$) wie folgt berechnet:
unter Verwendung von die Oberfläche, die Auftrieb erzeugt ($S_w$) und der Koeffizient Fahrstuhl ($C_L$).
Mit beiden Kr ften k nnen wir den erforderlichen Anstellwinkel f r den Gleitflug wie folgt bestimmen:
Beispiele
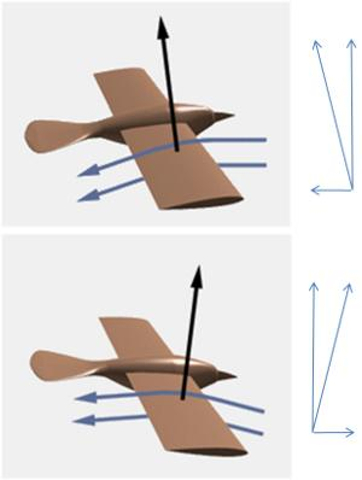
Eine Methode des Fliegens nennt sich Gleiten. Bei dieser Technik werden die Fl gel sowohl f r den Vortrieb als auch f r das Verbleiben in der Luft genutzt. Um dies zu erreichen, ist es notwendig, den Anstellwinkel des Fl gels so einzustellen, dass die Auftriebskraft der Schwerkraft entgegenwirkt. Das Gleiten wird somit zu einem kontrollierten Abstieg, bei dem der Abstieg genutzt wird, um Auftrieb zu erzeugen und dadurch die Geschwindigkeit auf kontrollierte Weise zu reduzieren.
Der Schl ssel zum Gleiten besteht darin, das Flugzeug oder den Vogel nach vorne zu kippen, das hei t, einen negativen Winkel zu haben, dargestellt durch ERROR:6121,0. Mit diesem negativen Winkel zeigt der die Auftriebskraft ($F_L$) Vektor nach oben und vorw rts anstatt nach hinten. Dies resultiert in einer Zugkraft anstelle von die Widerstandskraft ($F_W$), die das Flugzeug oder den Vogel antreibt und Geschwindigkeit erzeugt, was wiederum den notwendigen Auftrieb erzeugt.
Dieser Mechanismus erm glicht das Fliegen, aber es ist wichtig zu verstehen, dass es im Grunde genommen ein langsamer und kontrollierter Abstieg ist, da kein vollst ndig vertikaler eine Auftriebskraft ($F_L$) erreicht wird, um das Eigengewicht vollst ndig auszugleichen. Daher ist es notwendig, den Gleiter auf hohe H hen zu bringen oder dem Vogel zu erm glichen, anf ngliche H he durch seine eigene Antriebskraft zu gewinnen. Danach suchen beide nach aufsteigenden Luftstr mungen, die es ihnen erm glichen, innerhalb eines Aufwindes zu gleiten, der st rker ist als die Sinkgeschwindigkeit des Gleiters. Auf diese Weise k nnen sie ber lange Zeitr ume in der Luft bleiben, ohne landen zu m ssen.
In hnlicher Weise, wie der Anstellwinkel eines Flügels ($\alpha$) als der Winkel zwischen der Mittellinie des Fl gels und dem Horizont definiert ist, kann sein negatives Gegenst ck als der Gleitwinkel ($\phi$) festgelegt werden.
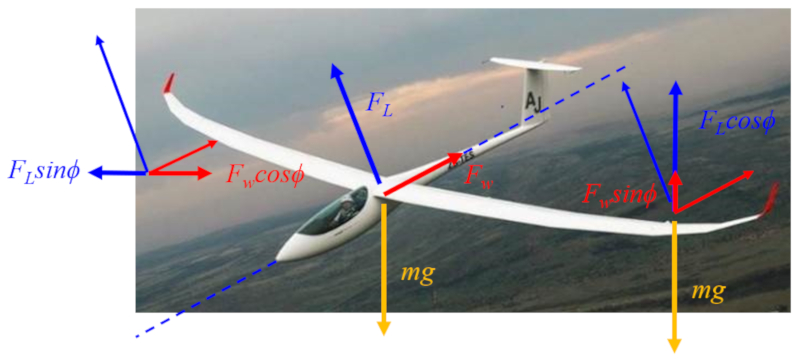
In Bezug auf die Kr fte haben wir folgende Aktionen:
• die Auftriebskraft ($F_L$) wirkt senkrecht zur Achse des Flugzeugs oder Vogels.
• die Widerstandskraft ($F_W$) wirkt entlang der Achse des Flugzeugs oder Vogels.
• die Erdanziehungskraft ($F_g$) ($mg$) wirkt vertikal.
Diese drei Kr fte sind in der Mitte des Diagramms dargestellt:
Auf der linken Seite sieht man die horizontale Komponente, bei der der Auftrieb den Luftwiderstand ausgleicht und als Schub wirkt.
Auf der rechten Seite sind die vertikalen Komponenten zu sehen, bei denen beide aerodynamischen Kr fte (Auftrieb und Luftwiderstand) dem Gewicht entgegenwirken, das auf den Schwerpunkt wirkt.
Obwohl sich die Kr fte gegenseitig aufheben, sinkt der Segelflieger, da seine Flugrichtung durch den Gleitwinkel bestimmt wird.
Der Planungswinkel ist der Neigungswinkel, in dem die horizontale Komponente der Zugkraft der horizontalen Reibung entgegenwirkt, w hrend die Summe aus Unterst tzung und Reibung in vertikaler Richtung der Schwerkraft entgegenwirkt. Diese Situation erm glicht einen Abstieg mit einem Winkel, der dem Gleitwinkel entspricht, der klein sein kann und einen sehr langsamen Abstieg erm glicht.
Wenn wir die Auftriebskraft ($F_L$), die Widerstandskraft ($F_W$), die Körpermasse ($m$), die Gravitationsbeschleunigung ($g$) und der Gleitwinkel ($\phi$) in Betracht ziehen, ist die Kraft beim Gleiten in vertikaler Richtung:
und in horizontaler Richtung:
Dadurch k nnen wir die Auftriebskraft ($F_L$) eliminieren, was zu folgendem f hrt:
$F_L=F_W\displaystyle\frac{\cos\phi}{\sin\phi} \rightarrow F_W(\sin^2\phi+\cos^2\phi)=mg\sin\phi$
die Widerstandskraft ($F_W$) sollte sein:
Wenn wir die Auftriebskraft ($F_L$), die Widerstandskraft ($F_W$), die Körpermasse ($m$), die Gravitationsbeschleunigung ($g$) und der Gleitwinkel ($\phi$) in Betracht ziehen, ist die Kraft beim Gleiten in vertikaler Richtung:
und in horizontaler Richtung:
Dadurch k nnen wir die Widerstandskraft ($F_W$) eliminieren, was zu folgendem f hrt:
$F_L=F_W\displaystyle\frac{\cos\phi}{\sin\phi} \rightarrow F_W(\sin^2\phi+\cos^2\phi)=mg\sin\phi$
Daher ist die Auftriebskraft ($F_L$):
Betrachten wir die Auftriebskraft ($F_L$), die Widerstandskraft ($F_W$), die Körpermasse ($m$), die Gravitationsbeschleunigung ($g$) und der Gleitwinkel ($\phi$). Mit diesen Kr ften wird die Auftriebskraft wie folgt berechnet:
und die Widerstandskraft wie folgt:
Wir k nnen der Gleitwinkel ($\phi$) bestimmen, indem wir die Auftriebskraft ($F_L$) durch die Widerstandskraft ($F_W$) teilen, was zu folgendem Ergebnis f hrt:
$\tan\phi=\displaystyle\frac{F_W}{F_L}$
Dabei wird die Widerstandskraft ($F_W$) mit folgender Gleichung berechnet:
unter Verwendung von der Gesamtobjektprofil ($S_p$) und der Widerstandskoeffizient ($C_W$). Ebenso wird die Auftriebskraft ($F_L$) wie folgt berechnet:
unter Verwendung von die Oberfläche, die Auftrieb erzeugt ($S_w$) und der Koeffizient Fahrstuhl ($C_L$).
Mit beiden Kr ften k nnen wir den erforderlichen Anstellwinkel f r den Gleitflug wie folgt bestimmen:
Im Falle des Gleitflugs besteht das Ziel darin, eine konstante Geschwindigkeit aufrechtzuerhalten, weshalb die Auftriebskraft ($F_L$) ausreichenden Vortrieb erzeugen muss, um die Widerstandskraft ($F_W$) auszugleichen.
Um dieses ERROR:6120,0 zu erreichen, erzeugt der Vogel oder das Flugzeug einen negativen ein Anstellwinkel eines Flügels ($\alpha$), was bedeutet, dass ein Teil von die Auftriebskraft ($F_L$) in Schub umgewandelt wird. Diese Kraftkomponente entspricht dem Sinus des Winkels.
Die Neigung f hrt auch zu einer Verringerung von die Widerstandskraft ($F_W$), da ein Teil davon zum Auftrieb beitr gt. In diesem Fall ist die Komponente, die immer noch zum Widerstand beitr gt, diese Kraft multipliziert mit dem Kosinus des Winkels.
Daher kann die Gleichung der Kraft in der horizontalen Ebene wie folgt ausgedr ckt werden:
Anstelle von der Anstellwinkel eines Flügels ($\alpha$) werden wir mit der Gleitwinkel ($\phi$) arbeiten.
Im vertikalen Flugzeug bewirkt der Gleitwinkel ($\phi$) eine Reduzierung von die Auftriebskraft ($F_L$) um einen Faktor gleich dem Kosinus des Winkels. Andererseits bewirkt es, dass die Widerstandskraft ($F_W$) mit einem Faktor gleich dem Sinus des Winkels zur Auftriebskraft beitr gt. Beide Kr fte m ssen das Gewicht ausgleichen, das von die Körpermasse ($m$) und die Gravitationsbeschleunigung ($g$) erzeugt wird, daher ergibt sich:
Die Auftriebskraft ($F_L$) ist mit die Körpermasse ($m$), die Gravitationsbeschleunigung ($g$) und der Gleitwinkel ($\phi$) gleich:
Die Widerstandskraft ($F_W$) ist mit die Körpermasse ($m$), die Gravitationsbeschleunigung ($g$) und der Gleitwinkel ($\phi$) gleich:
Die Auftriebskraft ($F_L$) und die Widerstandskraft ($F_W$) h ngen von die Körpermasse ($m$), die Gravitationsbeschleunigung ($g$) und der Gleitwinkel ($\phi$) ab. Beide Gleichungen erlauben es uns, der Gleitwinkel ($\phi$) in Bezug auf die Auftriebskraft ($F_L$) und die Widerstandskraft ($F_W$) zu berechnen.
Da die Auftriebskraft ($F_L$) und die Widerstandskraft ($F_W$) Funktionen von die Körpermasse ($m$), die Geschwindigkeit in Bezug auf das Medium ($v$), die Oberfläche, die Auftrieb erzeugt ($S_w$), der Gesamtobjektprofil ($S_p$), der Koeffizient Fahrstuhl ($C_L$) und der Widerstandskoeffizient ($C_W$) sind, k nnen wir zeigen, dass der Gleitwinkel ($\phi$) wie folgt ist:
Um einen h heren Druck unterhalb als oberhalb des Fl gels zu erzeugen und Auftrieb zu generieren, wird das Bernoulli-Prinzip angewendet und die fehlende Energieerhaltungsdichte durch ein Koeffizient Fahrstuhl ($C_L$) korrigiert. Der Druck ber dem Fl gel, die Auftriebskraft ($F_L$), kann unter Verwendung von die Dichte ($\rho$), die Oberfläche, die Auftrieb erzeugt ($S_w$), der Koeffizient Fahrstuhl ($C_L$) und die Geschwindigkeit in Bezug auf das Medium ($v$) mithilfe der folgenden Formel gesch tzt werden:
Die Widerstandskraft ($F_W$) se puede utilizar con die Dichte ($\rho$), der Widerstandskoeffizient ($C_W$), der Gesamtobjektprofil ($S_p$) y die Geschwindigkeit in Bezug auf das Medium ($v$) de acuerdo con la siguiente f rmula:
ID:(466, 0)