Gliding
Storyboard 
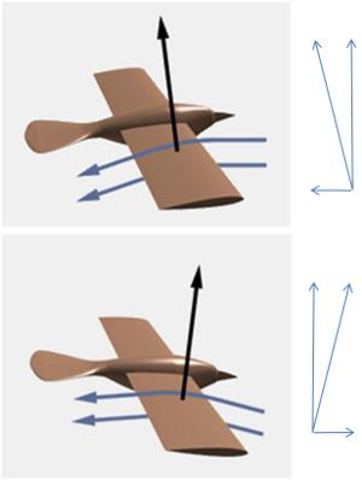
If the object (airplane / bird) maintains a slightly negative angle of attack, it can make part of the lifting force contribute to boost by countering the resistance. On the average that the remaining lift is not much less than the force of gravity, the object is long maintained in the air. You can talk about an extremely slow controlled descent or glide.
ID:(466, 0)
Gliding
Storyboard 
If the object (airplane / bird) maintains a slightly negative angle of attack, it can make part of the lifting force contribute to boost by countering the resistance. On the average that the remaining lift is not much less than the force of gravity, the object is long maintained in the air. You can talk about an extremely slow controlled descent or glide.
Variables
Calculations
Calculations
Equations
The lift force ($F_L$), along with the wing span ($L$), the density ($\rho$), the wing top speed factor ($c_t$), the wing bottom speed factor ($c_b$), the upper wing length ($l_t$), the bottom wing length ($l_b$), and the speed with respect to the medium ($v$), is found in
If we consider the surface that generates lift ($S_w$), given by the wing span ($L$), the upper wing length ($l_t$), and the bottom wing length ($l_b$),
and for the coefficient of lift ($C_L$), defined as
we obtain
Similarly to how the equation for the lift force ($F_L$) was derived using the density ($\rho$), the coefficient of lift ($C_L$), the surface that generates lift ($S_w$), and the speed with respect to the medium ($v$)
in this analogy, what corresponds to the surface that generates lift ($S_w$) will be equivalent to the total object profile ($S_p$) and the coefficient of lift ($C_L$) to the coefficient of resistance ($C_W$), thus the resistance force ($F_W$) is calculated:
The drag coefficient is measured and, in turbulent flows over aerodynamic bodies, values are generally found around 0.4.
If we consider the lift force ($F_L$), the resistance force ($F_W$), the body mass ($m$), the gravitational Acceleration ($g$), and the glide angle ($\phi$), the force during gliding in the vertical direction is:
and in the horizontal direction:
This allows us to eliminate the resistance force ($F_W$), resulting in:
$F_L=F_W\displaystyle\frac{\cos\phi}{\sin\phi} \rightarrow F_W(\sin^2\phi+\cos^2\phi)=mg\sin\phi$
Therefore, the lift force ($F_L$) is:
If we consider the lift force ($F_L$), the resistance force ($F_W$), the body mass ($m$), the gravitational Acceleration ($g$), and the glide angle ($\phi$), the force during gliding in the vertical direction is:
and in the horizontal direction is:
This allows us to eliminate the lift force ($F_L$), resulting in:
$F_L=F_W\displaystyle\frac{\cos\phi}{\sin\phi} \rightarrow F_W(\sin^2\phi+\cos^2\phi)=mg\sin\phi$
the resistance force ($F_W$) should be:
Let's consider the lift force ($F_L$), the resistance force ($F_W$), the body mass ($m$), the gravitational Acceleration ($g$), and the glide angle ($\phi$). With these forces, the lift force is calculated as:
and the drag force as:
We can determine the glide angle ($\phi$) by dividing the lift force ($F_L$) by the resistance force ($F_W$), resulting in:
$\tan\phi=\displaystyle\frac{F_W}{F_L}$
Where the resistance force ($F_W$) is calculated using the equation:
with the total object profile ($S_p$) and the coefficient of resistance ($C_W$). Similarly, the lift force ($F_L$) is calculated as:
with the surface that generates lift ($S_w$) and the coefficient of lift ($C_L$).
With both forces, we can determine the necessary angle of attack for gliding as:
Examples
One method of flying is known as gliding. In this technique, the wings are used both for propulsion and to remain airborne. To achieve this, it is necessary to adjust the wing's angle of attack in a way that the lift force counteracts gravity. As a result, gliding becomes a controlled descent where the descent is used to generate lift and thereby reduce speed in a controlled manner.
The key to gliding is to tilt the aircraft or bird forward, in other words, to have a negative angle represented by ERROR:6121,0. With this negative angle, the the lift force ($F_L$) vector points upward and forward instead of backward. This results in a pulling force rather than the resistance force ($F_W$), propelling the aircraft or bird and generating speed, which, in turn, creates the necessary lift.
This mechanism allows for flight, but it's essential to understand that it's essentially a slow and controlled descent since it doesn't achieve a completely vertical a lift force ($F_L$) to counteract its own weight. Therefore, it's necessary to take the glider to high altitudes or allow the bird to gain initial height through its own propulsion. Afterward, both seek ascending air currents that enable them to glide within an updraft stronger than the glider's descent rate. This way, they can remain in flight for extended periods without the need to land.
Similarly to how the angle of attack of a wing ($\alpha$) is defined as the angle between the wing's centerline and the horizon, its negative counterpart can be defined as the glide angle ($\phi$).
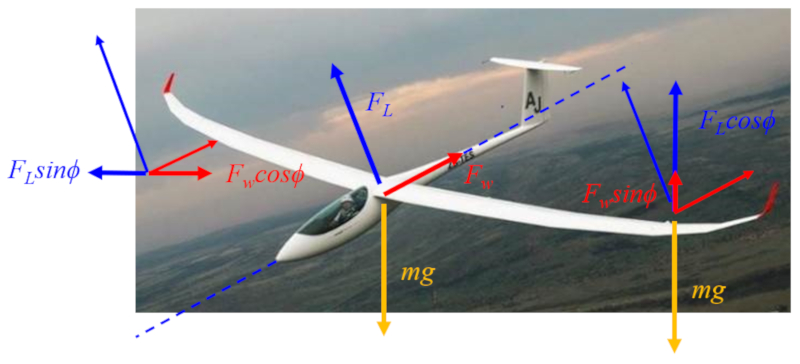
When it comes to forces, we have the following actions:
• the lift force ($F_L$) acts perpendicularly to the aircraft or bird's axis.
• the resistance force ($F_W$) acts along the aircraft or bird's axis.
• the gravitational force ($F_g$) ($mg$) acts vertically.
These three forces are depicted at the center of the diagram:
On the left side, you can see the horizontal component, where lift counters the drag, acting as thrust.
On the right side, the vertical components are visible, where both aerodynamic forces (lift and drag) oppose the weight acting on the center of mass.
Although the forces balance each other out, the glider descends because its flight direction is determined by the glide angle.
The angle of planning is that angle of inclination in which the horizontal component of the traction force counteracts the horizontal friction while the sum of the support and friction in the vertical direction counteracts the force of gravity. This situation allows a descent with an angle equal to the gliding angle that can be small allowing a very slow descent.
If we consider the lift force ($F_L$), the resistance force ($F_W$), the body mass ($m$), the gravitational Acceleration ($g$), and the glide angle ($\phi$), the force during gliding in the vertical direction is:
and in the horizontal direction is:
This allows us to eliminate the lift force ($F_L$), resulting in:
$F_L=F_W\displaystyle\frac{\cos\phi}{\sin\phi} \rightarrow F_W(\sin^2\phi+\cos^2\phi)=mg\sin\phi$
the resistance force ($F_W$) should be:
If we consider the lift force ($F_L$), the resistance force ($F_W$), the body mass ($m$), the gravitational Acceleration ($g$), and the glide angle ($\phi$), the force during gliding in the vertical direction is:
and in the horizontal direction:
This allows us to eliminate the resistance force ($F_W$), resulting in:
$F_L=F_W\displaystyle\frac{\cos\phi}{\sin\phi} \rightarrow F_W(\sin^2\phi+\cos^2\phi)=mg\sin\phi$
Therefore, the lift force ($F_L$) is:
Let's consider the lift force ($F_L$), the resistance force ($F_W$), the body mass ($m$), the gravitational Acceleration ($g$), and the glide angle ($\phi$). With these forces, the lift force is calculated as:
and the drag force as:
We can determine the glide angle ($\phi$) by dividing the lift force ($F_L$) by the resistance force ($F_W$), resulting in:
$\tan\phi=\displaystyle\frac{F_W}{F_L}$
Where the resistance force ($F_W$) is calculated using the equation:
with the total object profile ($S_p$) and the coefficient of resistance ($C_W$). Similarly, the lift force ($F_L$) is calculated as:
with the surface that generates lift ($S_w$) and the coefficient of lift ($C_L$).
With both forces, we can determine the necessary angle of attack for gliding as:
In the case of gliding, the goal is to maintain a constant velocity, so the lift force ($F_L$) must generate sufficient propulsion to counteract the resistance force ($F_W$).
To achieve this ERROR:6120,0, the bird or aircraft generates a negative a angle of attack of a wing ($\alpha$), which means that part of the lift force ($F_L$) is converted into thrust. This component of force is equal to the sine of the angle.
The inclination also leads to a reduction in the resistance force ($F_W$), as a portion of it contributes to lift. In this case, the component that still contributes to resistance is this force multiplied by the cosine of the angle.
Therefore, the equation of force in the horizontal plane can be expressed as:
Instead of using the angle of attack of a wing ($\alpha$), we will work with the glide angle ($\phi$).
In the vertical plane, the glide angle ($\phi$) results in a reduction of the lift force ($F_L$) by a factor equal to the cosine of the angle. On the other hand, it causes the resistance force ($F_W$) to contribute to lift with a factor equal to the sine of the angle. Both forces must counteract the weight generated by the body mass ($m$) and the gravitational Acceleration ($g$), so we have:
The lift force ($F_L$) is with the body mass ($m$), the gravitational Acceleration ($g$) and the glide angle ($\phi$) equal to:
The resistance force ($F_W$) is with the body mass ($m$), the gravitational Acceleration ($g$) and the glide angle ($\phi$) equal to:
The lift force ($F_L$) and the resistance force ($F_W$) depend on the body mass ($m$), the gravitational Acceleration ($g$), and the glide angle ($\phi$). Both equations allow us to calculate the glide angle ($\phi$) in terms of the lift force ($F_L$) and the resistance force ($F_W$).
Since the lift force ($F_L$) and the resistance force ($F_W$) are functions of the body mass ($m$), the speed with respect to the medium ($v$), the surface that generates lift ($S_w$), the total object profile ($S_p$), the coefficient of lift ($C_L$), and the coefficient of resistance ($C_W$), we can demonstrate that the glide angle ($\phi$) is:
To generate higher pressure below than above the wing and generate lift, Bernoulli's principle is employed, correcting for the lack of energy density conservation using ERROR:6119.1. The pressure over the wing, the lift force ($F_L$), can be estimated using the density ($\rho$), the surface that generates lift ($S_w$), the coefficient of lift ($C_L$), and the speed with respect to the medium ($v$) through the following formula:
The resistance force ($F_W$) kann mit the density ($\rho$), the coefficient of resistance ($C_W$), the total object profile ($S_p$) und the speed with respect to the medium ($v$) entsprechend berechnet werden folgende Formel:
ID:(466, 0)