Flug
Storyboard 
Um in konstanter Höhe zu fliegen, muss das Objekt (Flugzeug / Vogel) den Anstellwinkel des Flügels an den Antrieb anpassen, um dem Gewicht entgegenzuwirken und die gewünschte Geschwindigkeit beizubehalten.
Variablen
Berechnungen
Berechnungen
Gleichungen
Die Auftriebskraft ($F_L$), zusammen mit die Spannweite der Flügel ($L$), die Dichte ($\rho$), der Flügel-Höchstgeschwindigkeitsfaktor ($c_t$), der Flügelbodengeschwindigkeitsfaktor ($c_b$), die Obere Flügellänge ($l_t$), die Länge des unteren Flügels ($l_b$) und die Geschwindigkeit in Bezug auf das Medium ($v$), findet sich in
Wenn wir die Oberfläche, die Auftrieb erzeugt ($S_w$) betrachten, gegeben durch die Spannweite der Flügel ($L$), die Obere Flügellänge ($l_t$) und die Länge des unteren Flügels ($l_b$),
und f r der Koeffizient Fahrstuhl ($C_L$), definiert als
erhalten wir
hnlich wie die Gleichung f r die Auftriebskraft ($F_L$) unter Verwendung von die Dichte ($\rho$), der Koeffizient Fahrstuhl ($C_L$), die Oberfläche, die Auftrieb erzeugt ($S_w$) und die Geschwindigkeit in Bezug auf das Medium ($v$) abgeleitet wurde
entspricht in dieser Analogie das, was die Oberfläche, die Auftrieb erzeugt ($S_w$) entspricht, der Gesamtobjektprofil ($S_p$) und der Koeffizient Fahrstuhl ($C_L$) entspricht der Widerstandskoeffizient ($C_W$), woraus die Widerstandskraft ($F_W$) berechnet wird:
Der Widerstandsbeiwert wird gemessen und bei turbulenten Str mungen ber aerodynamischen K rpern werden blicherweise Werte um 0,4 ermittelt.
Unter Verwendung der Beziehungen von die Gesamtwiderstandskraft ($F_R$) mit die Auftriebskraft ($F_L$), die Widerstandskraft ($F_W$) und der Anstellwinkel eines Flügels ($\alpha$) k nnen wir unter Verwendung der Widerstandskraft mit die Dichte ($\rho$), der Widerstandskoeffizient ($C_W$), der Gesamtobjektprofil ($S_p$) und die Geschwindigkeit in Bezug auf das Medium ($v$):
und der Auftriebskraft mit die Oberfläche, die Auftrieb erzeugt ($S_w$) und der Koeffizient Fahrstuhl ($C_L$):
unter Verwendung der Beziehung f r der Koeffizient Fahrstuhl ($C_L$) mit die Proportionalitätskonstante Koeffizient Nachhaltigkeit ($c$):
unter Verwendung der Beziehung f r den Sinus des kleinen Anstellwinkels $\alpha$:
und des Kosinus:
bei der Bedingung, das Gewicht des Vogels oder Flugzeugs f r die Körpermasse ($m$) und die Gravitationsbeschleunigung ($g$) auszubalancieren:
erhalten wir:
Die Leistung wird definiert als Energie $\Delta W$ pro Zeit $\Delta t$ gem der Gleichung:
Da die Energie gleich der Kraft $F$ multipliziert mit der zur ckgelegten Strecke $\Delta s$ ist, haben wir:
Daher erhalten wir:
$P=\displaystyle\frac{\Delta W}{\Delta t}= F_R \displaystyle\frac{\Delta s}{\Delta t}$
Da jedoch die zur ckgelegte Strecke in einem Zeitintervall die Geschwindigkeit $v$ ist:
Schlie lich k nnen wir den Ausdruck f r die Leistung wie folgt schreiben:
Die Gesamtwiderstandskraft ($F_R$) ist eine Funktion von die Dichte ($\rho$), die Oberfläche, die Auftrieb erzeugt ($S_w$), der Gesamtobjektprofil ($S_p$), der Widerstandskoeffizient ($C_W$), die Proportionalitätskonstante Koeffizient Nachhaltigkeit ($c$), die Körpermasse ($m$) und die Gravitationsbeschleunigung ($g$), was gleich ist
daher, unter Verwendung der Gleichung f r die Power of flight ($P$)
erhalten wir:
Die horizontale Komponente des Auftriebs entspricht der Kraft $F_L$ multipliziert mit dem Sinus des Anstellwinkels $\alpha$:
$F_L \sin\alpha $
und die horizontale Komponente des Widerstands entspricht der Kraft $F_W$ multipliziert mit dem Kosinus des Anstellwinkels $\alpha$:
$F_W \cos\alpha $
Daher wird die Gesamtwiderstandskraft wie folgt berechnet:
Beispiele
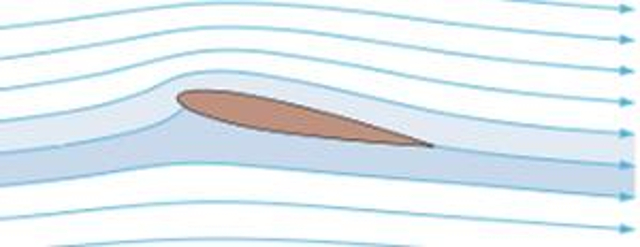
Wenn wir annehmen, dass der Str mung um einen Fl gel laminar ist, k nnen wir mehrere Schichten um den Fl gel herum beobachten. Diejenigen auf der Oberseite sind aufgrund der nach oben gerichteten Kr mmung tendenziell etwas l nger, w hrend die unteren Schichten tendenziell k rzer und daher n her am Fl gel sind.
Angenommen, die Str mung ist so, dass diese Schichten konvergieren, sodass Punkte auf beiden Seiten des Fl gels, die nah beieinander liegen, nach dem Abl sen der Str mung wieder in die gleiche relative Position zur ckkehren, wird die Geschwindigkeit der oberen Schichten zwangsl ufig h her sein als die der unteren Schichten. Es ist wichtig zu beachten, dass dies nur eine Annahme ist, und es besteht keine echte Notwendigkeit f r eine Konvergenz; tats chlich k nnten sie ohne Probleme auch aus dem Takt geraten.
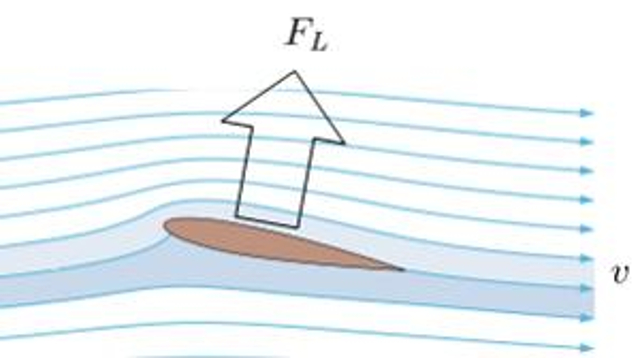
Da die Geschwindigkeit in den oberen Schichten des Fl gels gr er ist als in den unteren Schichten, dass der Druck auf der Oberseite des Fl gels geringer ist als auf der Unterseite.
Das bedeutet effektiv, dass von unten auf den Fl gel eine gr ere Kraft wirkt als von oben, was zur Erzeugung einer Auftriebskraft f hrt.
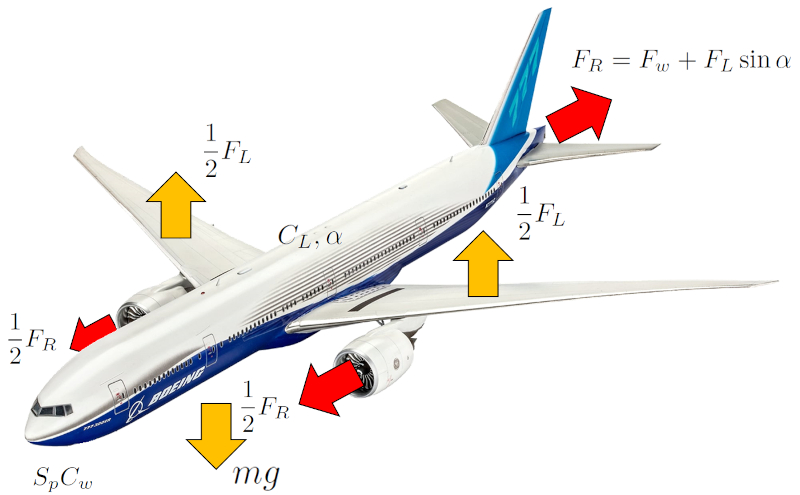
Die Kr fte, die auf ein Flugzeug oder einen Vogel einwirken, k nnen in zwei grundlegende Kategorien unterteilt werden:
Kr fte, die die Kontrolle ber die Bewegung des Schwerpunkts beeinflussen:
• die Auftriebskraft ($F_L$), die die Erdanziehungskraft ($F_g$) entgegenwirkt.
• die Antriebskraft ($F_p$), die die Widerstandskraft ($F_W$) entgegenwirkt.
Kr fte zur Erzielung der Rotation des Flugzeugs oder Vogels um den Schwerpunkt, die durch die Querruder an den Fl geln und das Seitenruder erreicht werden:
• Die Querruder erm glichen die Erzeugung eines Drehmoments, indem sie den Auftrieb an jedem Fl gel asymmetrisch ver ndern.
• Das Seitenruder steuert die Richtung des Flugzeugs oder Vogels, indem es den Luftstrom umlenkt.
Wichtige Parameter zur Steuerung der Bewegung des Schwerpunkts sind:
• die Oberfläche, die Auftrieb erzeugt ($S_w$) und der Gesamtobjektprofil ($S_p$).
• der Koeffizient Fahrstuhl ($C_L$) und der Widerstandskoeffizient ($C_W$), wobei letzteres von der Anstellwinkel eines Flügels ($\alpha$) abh ngt.
Die Schwerkraft ($F_g$) basiert auf die Gravitationsmasse ($m_g$) des Objekts und auf einer Konstanten, die die Intensit t der Gravitation an der Oberfl che des Planeten widerspiegelt. Letztere wird durch die Gravitationsbeschleunigung ($g$) identifiziert, was $9.8 m/s^2$ entspricht.
Daraus folgt, dass:
Um einen h heren Druck unterhalb als oberhalb des Fl gels zu erzeugen und Auftrieb zu generieren, wird das Bernoulli-Prinzip angewendet und die fehlende Energieerhaltungsdichte durch ein Koeffizient Fahrstuhl ($C_L$) korrigiert. Der Druck ber dem Fl gel, die Auftriebskraft ($F_L$), kann unter Verwendung von die Dichte ($\rho$), die Oberfläche, die Auftrieb erzeugt ($S_w$), der Koeffizient Fahrstuhl ($C_L$) und die Geschwindigkeit in Bezug auf das Medium ($v$) mithilfe der folgenden Formel gesch tzt werden:
Um die Gesamtwiderstandskraft ($F_R$) zu berechnen, gehen wir von kleinen Winkeln aus und betrachten eine Situation, in der der Winkel so beschaffen ist, dass er die Körpermasse ($m$) beibeh lt. Unter Verwendung dieser Annahme und der Variablen der Koeffizient Fahrstuhl ($C_L$), der Widerstandskoeffizient ($C_W$), die Oberfläche, die Auftrieb erzeugt ($S_w$), der Gesamtobjektprofil ($S_p$), die Gravitationsbeschleunigung ($g$), die Proportionalitätskonstante Koeffizient Nachhaltigkeit ($c$), die Dichte ($\rho$) und die Geschwindigkeit in Bezug auf das Medium ($v$) erhalten wir den folgenden Ausdruck:
Die Gesamtwiderstandskraft setzt sich aus den horizontalen Komponenten der Widerstandskraft des Profils des Fl gels $F_W$ und der Auftriebskraft $F_L$ zusammen, die aus dem Anstellwinkel $\alpha$ berechnet werden k nnen:
Die Widerstandskraft ($F_W$) se puede utilizar con die Dichte ($\rho$), der Widerstandskoeffizient ($C_W$), der Gesamtobjektprofil ($S_p$) y die Geschwindigkeit in Bezug auf das Medium ($v$) de acuerdo con la siguiente f rmula:
Die Leistung $P$ ist die Energie pro Zeiteinheit, die aufgebracht werden muss, um eine gegebene Kraft $F_R$ aufrechtzuerhalten. Daher kann sie durch Multiplikation der Kraft mit der Geschwindigkeit $v$ berechnet werden:
Um die Power of flight ($P$) zu erhalten, muss man die Gesamtwiderstandskraft ($F_R$) mit die Geschwindigkeit in Bezug auf das Medium ($v$) multiplizieren. Da die Gesamtwiderstandskraft ($F_R$) eine Funktion von die Dichte ($\rho$), die Oberfläche, die Auftrieb erzeugt ($S_w$), der Gesamtobjektprofil ($S_p$), der Widerstandskoeffizient ($C_W$), die Proportionalitätskonstante Koeffizient Nachhaltigkeit ($c$), die Körpermasse ($m$) und die Gravitationsbeschleunigung ($g$) ist, was gleich ist:
ergibt sich das Potenzial als
ID:(1463, 0)