Planifier
Storyboard 
Si l'objet (avion/oiseau) maintient un angle d'attaque légèrement négatif, il peut faire en sorte que partie de la force de portance contribue à la poussée en contrant la traînée. Tant que la portance restante n'est pas nettement inférieure à la force de gravité, l'objet peut rester en l'air pendant une période prolongée. On peut parler d'une descente contrôlée extrêmement lente ou de planeur.
ID:(466, 0)
Planifier
Storyboard 
Si l'objet (avion/oiseau) maintient un angle d'attaque légèrement négatif, il peut faire en sorte que partie de la force de portance contribue à la poussée en contrant la traînée. Tant que la portance restante n'est pas nettement inférieure à la force de gravité, l'objet peut rester en l'air pendant une période prolongée. On peut parler d'une descente contrôlée extrêmement lente ou de planeur.
Variables
Calculs
Calculs
Équations
A force de levage ($F_L$), en compagnie de a envergure des ailes ($L$), a densité ($\rho$), le facteur de vitesse maximale de l'aile ($c_t$), le facteur de vitesse en bas d'aile ($c_b$), a longueur de l'aile supérieure ($l_t$), a longueur de l'aile inférieure ($l_b$) et a vitesse par rapport au milieu ($v$), se trouve dans
Si nous consid rons a surface génératrice de portance ($S_w$), d fini par a envergure des ailes ($L$), a longueur de l'aile supérieure ($l_t$) et a longueur de l'aile inférieure ($l_b$),
et pour le coefficient de portance ($C_L$), d fini comme
nous obtenons
De mani re similaire la fa on dont l' quation pour a force de levage ($F_L$) a t d riv e en utilisant a densité ($\rho$), le coefficient de portance ($C_L$), a surface génératrice de portance ($S_w$) et a vitesse par rapport au milieu ($v$)
dans cette analogie, ce qui correspond a surface génératrice de portance ($S_w$) sera quivalent le profil total de l'objet ($S_p$) et le coefficient de portance ($C_L$) Le coefficient de résistance ($C_W$), ce qui permet de calculer a force de résistance ($F_W$) :
Le coefficient de tra n e est mesur et, dans les coulements turbulents sur les corps a rodynamiques, les valeurs sont g n ralement autour de 0.4.
Si nous consid rons a force de levage ($F_L$), a force de résistance ($F_W$), a masse corporelle ($m$), a accélération gravitationnelle ($g$) et le angle de plané ($\phi$), la force lors du planeur dans la direction verticale est :
et dans la direction horizontale :
Cela nous permet d' liminer a force de résistance ($F_W$), ce qui donne :
$F_L=F_W\displaystyle\frac{\cos\phi}{\sin\phi} \rightarrow F_W(\sin^2\phi+\cos^2\phi)=mg\sin\phi$
Par cons quent, a force de levage ($F_L$) est :
Si nous consid rons a force de levage ($F_L$), a force de résistance ($F_W$), a masse corporelle ($m$), a accélération gravitationnelle ($g$) et le angle de plané ($\phi$), la force lors du planeur dans la direction verticale est :
et dans la direction horizontale est :
Cela nous permet d' liminer a force de levage ($F_L$), r sultant en :
$F_L=F_W\displaystyle\frac{\cos\phi}{\sin\phi} \rightarrow F_W(\sin^2\phi+\cos^2\phi)=mg\sin\phi$
a force de résistance ($F_W$) devrait tre :
Consid rons a force de levage ($F_L$), a force de résistance ($F_W$), a masse corporelle ($m$), a accélération gravitationnelle ($g$) et le angle de plané ($\phi$). Avec ces forces, la force de portance est calcul e comme suit :
et la force de tra n e comme suit :
Nous pouvons d terminer le angle de plané ($\phi$) en divisant a force de levage ($F_L$) par a force de résistance ($F_W$), ce qui donne :
$\tan\phi=\displaystyle\frac{F_W}{F_L}$
O A force de résistance ($F_W$) est calcul l'aide de l' quation suivante :
avec le profil total de l'objet ($S_p$) et le coefficient de résistance ($C_W$). De m me, a force de levage ($F_L$) est calcul comme suit :
avec a surface génératrice de portance ($S_w$) et le coefficient de portance ($C_L$).
Avec ces deux forces, nous pouvons d terminer l'angle d'attaque n cessaire pour le planeur comme suit :
Exemples
Une m thode de vol est connue sous le nom de vol voile. Dans cette technique, les ailes sont utilis es la fois pour la propulsion et pour rester en l'air. Pour y parvenir, il est n cessaire d'ajuster l'angle d'attaque de l'aile de mani re ce que la force de portance contrebalance la gravit . En cons quence, le vol voile devient une descente contr l e o la descente est utilis e pour g n rer de la portance et ainsi r duire la vitesse de mani re contr l e.
La cl du vol plan consiste incliner l'avion ou l'oiseau vers l'avant, c'est- -dire avoir un angle n gatif repr sent par ERROR:6121,0. Avec cet angle n gatif, le vecteur a force de levage ($F_L$) pointe vers le haut et vers l'avant au lieu de vers l'arri re. Cela r sulte en une force de traction plut t qu'en a force de résistance ($F_W$), propulsant ainsi l'avion ou l'oiseau et g n rant de la vitesse, ce qui son tour cr e la portance n cessaire.
Ce m canisme permet le vol, mais il est essentiel de comprendre qu'il s'agit essentiellement d'une descente lente et contr l e, car il n'atteint pas un une force de levage ($F_L$) vertical pour compenser compl tement son propre poids. Par cons quent, il est n cessaire de monter le planeur de hautes altitudes ou de permettre l'oiseau de gagner de la hauteur initialement gr ce sa propre propulsion. Ensuite, les deux cherchent des courants ascendants qui leur permettent de planer l'int rieur d'une ascendance plus forte que la vitesse de descente du planeur. De cette mani re, ils peuvent rester en vol pendant de longues p riodes sans avoir besoin d'atterrir.
De mani re similaire la d finition de le accélération maximale ($\alpha$) comme l'angle entre la ligne m diane de l'aile et l'horizon, son quivalent n gatif peut tre d fini comme le angle de plané ($\phi$).
En ce qui concerne les forces, nous avons les actions suivantes :
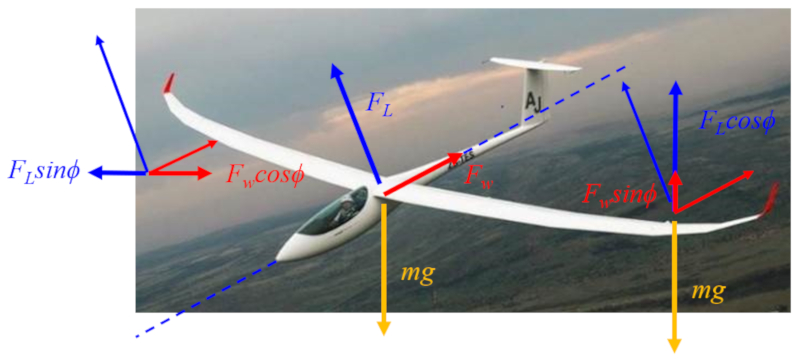
• a force de levage ($F_L$) agit perpendiculairement l'axe de l'avion ou de l'oiseau.
• a force de résistance ($F_W$) agit le long de l'axe de l'avion ou de l'oiseau.
• a force gravitationnelle ($F_g$) ($mg$) agit verticalement.
Ces trois forces sont repr sent es au centre du sch ma :
Sur le c t gauche, vous pouvez voir la composante horizontale, o la portance contrecarre la tra n e, agissant comme une pouss e.
Sur le c t droit, les composantes verticales sont visibles, o les deux forces a rodynamiques (portance et tra n e) s'opposent au poids agissant sur le centre de masse.
Bien que les forces s' quilibrent mutuellement, le planeur descend car sa direction de vol est d termin e par l'angle de plan.
Si nous consid rons a force de levage ($F_L$), a force de résistance ($F_W$), a masse corporelle ($m$), a accélération gravitationnelle ($g$) et le angle de plané ($\phi$), la force lors du planeur dans la direction verticale est :
et dans la direction horizontale est :
Cela nous permet d' liminer a force de levage ($F_L$), r sultant en :
$F_L=F_W\displaystyle\frac{\cos\phi}{\sin\phi} \rightarrow F_W(\sin^2\phi+\cos^2\phi)=mg\sin\phi$
a force de résistance ($F_W$) devrait tre :
Si nous consid rons a force de levage ($F_L$), a force de résistance ($F_W$), a masse corporelle ($m$), a accélération gravitationnelle ($g$) et le angle de plané ($\phi$), la force lors du planeur dans la direction verticale est :
et dans la direction horizontale :
Cela nous permet d' liminer a force de résistance ($F_W$), ce qui donne :
$F_L=F_W\displaystyle\frac{\cos\phi}{\sin\phi} \rightarrow F_W(\sin^2\phi+\cos^2\phi)=mg\sin\phi$
Par cons quent, a force de levage ($F_L$) est :
Consid rons a force de levage ($F_L$), a force de résistance ($F_W$), a masse corporelle ($m$), a accélération gravitationnelle ($g$) et le angle de plané ($\phi$). Avec ces forces, la force de portance est calcul e comme suit :
et la force de tra n e comme suit :
Nous pouvons d terminer le angle de plané ($\phi$) en divisant a force de levage ($F_L$) par a force de résistance ($F_W$), ce qui donne :
$\tan\phi=\displaystyle\frac{F_W}{F_L}$
O A force de résistance ($F_W$) est calcul l'aide de l' quation suivante :
avec le profil total de l'objet ($S_p$) et le coefficient de résistance ($C_W$). De m me, a force de levage ($F_L$) est calcul comme suit :
avec a surface génératrice de portance ($S_w$) et le coefficient de portance ($C_L$).
Avec ces deux forces, nous pouvons d terminer l'angle d'attaque n cessaire pour le planeur comme suit :
Dans le cas du vol plan , l'objectif est de maintenir une vitesse constante, ce qui signifie que a force de levage ($F_L$) doit g n rer une propulsion suffisante pour contrer a force de résistance ($F_W$).
Pour atteindre cette ERROR:6120,0, l'oiseau ou l'a ronef g n re un un accélération maximale ($\alpha$) n gatif, ce qui signifie qu'une partie de a force de levage ($F_L$) est convertie en pouss e. Cette composante de force est gale au sinus de l'angle.
L'inclinaison entra ne galement une r duction de a force de résistance ($F_W$), car une partie de celle-ci contribue la portance. Dans ce cas, la composante qui contribue toujours la r sistance est cette force multipli e par le cosinus de l'angle.
Par cons quent, l' quation de la force dans le plan horizontal peut tre exprim e comme suit :
Au lieu d'utiliser le accélération maximale ($\alpha$), nous travaillerons avec le angle de plané ($\phi$).
Dans le plan vertical, le angle de plané ($\phi$) entra ne une r duction de a force de levage ($F_L$) par un facteur gal au cosinus de l'angle. D'autre part, il fait en sorte que a force de résistance ($F_W$) contribue la portance avec un facteur gal au sinus de l'angle. Les deux forces doivent compenser le poids g n r par a masse corporelle ($m$) et a accélération gravitationnelle ($g$), donc nous obtenons :
A force de levage ($F_L$) est avec a masse corporelle ($m$), a accélération gravitationnelle ($g$) et le angle de plané ($\phi$) gal xa0:
A force de résistance ($F_W$) est avec a masse corporelle ($m$), a accélération gravitationnelle ($g$) et le angle de plané ($\phi$) gal xa0:
A force de levage ($F_L$) et a force de résistance ($F_W$) d pendent de a masse corporelle ($m$), a accélération gravitationnelle ($g$) et le angle de plané ($\phi$). Les deux quations nous permettent de calculer le angle de plané ($\phi$) en fonction de a force de levage ($F_L$) et a force de résistance ($F_W$).
tant donn que a force de levage ($F_L$) et a force de résistance ($F_W$) sont des fonctions de a masse corporelle ($m$), a vitesse par rapport au milieu ($v$), a surface génératrice de portance ($S_w$), le profil total de l'objet ($S_p$), le coefficient de portance ($C_L$) et le coefficient de résistance ($C_W$), nous pouvons d montrer que le angle de plané ($\phi$) est :
Pour g n rer une pression plus lev e en dessous qu'au-dessus de l'aile et produire de la portance, le principe de Bernoulli est utilis pour corriger le manque de conservation de la densit d' nergie avec un coefficient de portance ($C_L$). La pression sur l'aile, a force de levage ($F_L$), peut tre estim e en utilisant a densité ($\rho$), a surface génératrice de portance ($S_w$), le coefficient de portance ($C_L$), et a vitesse par rapport au milieu ($v$) gr ce la formule suivante :
A force de résistance ($F_W$) peut tre calcul en utilisant a densité ($\rho$), le coefficient de résistance ($C_W$), le profil total de l'objet ($S_p$) et a vitesse par rapport au milieu ($v$) selon le formule suivante :
ID:(466, 0)