Benützer:
Kontrolle
Storyboard 
Zur Manövrierung des Flugzeugs werden Höhenruder, Querruder und das Seitenruder verwendet. Alle nutzen den Auftrieb, der durch das Profil des Flügels erzeugt wird, um Kräfte an entfernten Punkten vom Massenschwerpunkt zu erzeugen und somit Drehmomente zu induzieren, die das Flugzeug rotieren lassen.
ID:(2055, 0)
Kontrolle, Benutzung des Auftriebes
Konzept
Die Querruder sind Teile der Tragflächen, die es ermöglichen, den hinteren Rand nach oben (Erzeugung einer Abtriebskraft) oder nach unten (Erzeugung einer Auftriebskraft) zu krümmen. Sie befinden sich alle an Punkten, die weit vom Massenschwerpunkt entfernt sind, um einen größeren Abstand und somit ein größeres Drehmoment zu erreichen, was sie in der Rotation effektiver macht.
Aufgrund der Geometrie gibt es drei Achsen, um die sich das Flugzeug dreht. Das Ruder-Querruder erzeugt eine Drehung um eine vertikale Achse. Die Querruder an den kleineren hinteren Tragflächen (Stabilisatoren genannt) ermöglichen eine Drehung um eine Achse senkrecht zur Flugzeugachse, um die Nase des Flugzeugs anzuheben und abzusenken. Schließlich gibt es die Querruder an den Haupttragflächen, die es dem Flugzeug ermöglichen, sich um seine zentrale Achse zu drehen.
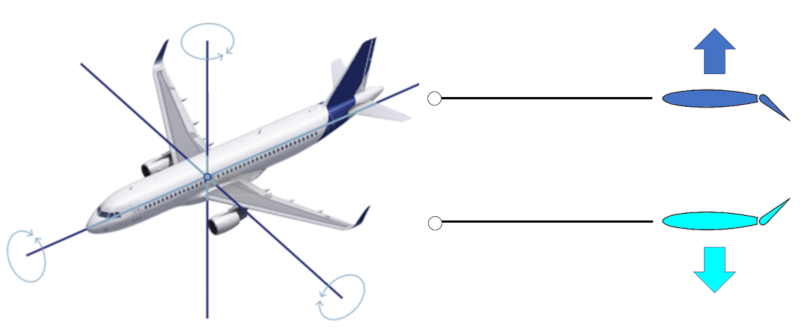
Es gibt eine Art von Querruder, die zusätzlich an den Haupttragflächen in der Nähe des Rumpfes ausfahrbar sind, bekannt als Klappen, die sowohl die Flügelfläche als auch den Anstellwinkel erhöhen/reduzieren.
Schließlich gibt es Oberflächen, die angehoben werden können, um den Luftstrom über der Tragfläche zu stören und als Bremsklappen verwendet werden, bekannt als Spoiler.
ID:(11081, 0)
Pitch-Kontrolle
Konzept
Um die Nase des Flugzeugs nach oben oder unten zu neigen, werden die Höhenruder verwendet. Beide Höhenruder werden symmetrisch eingesetzt, um eine die Kraft auf den Auftriebselementen ($F_e$) symmetrische Wirkung zu erzeugen. Indem sie am Heck des Flugzeugs platziert werden, wird eine ($$) größere Effektivität erzielt, da sie sich in der Nähe des Schwerpunkts befinden. Dies ermöglicht ausreichende Kontrolle, um die Nase des Flugzeugs anzuheben oder abzusenken.
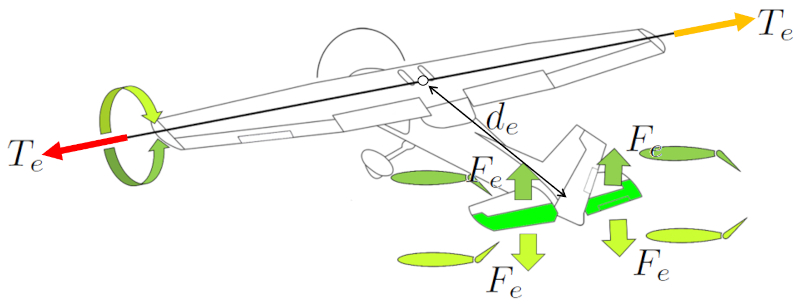
Bei älteren Flugzeugen erfolgt die Steuerung der hinteren Querruder über einen Steuerknüppel, bei dem das Drücken nach vorne dazu führt, dass die Nase des Flugzeugs sinkt, während das Ziehen nach hinten die Nase anhebt. Bei Flugzeugen der Airbus-Familie erfolgt diese Steuerung über einen Joystick.
Im Falle von Vögeln gibt es eine ähnliche Lösung, wobei der Schwanz jedoch nicht durch ein Seitenruder unterbrochen ist.
ID:(15161, 0)
Rollkontrolle
Konzept
Um eine Rollbewegung um ihre Längsachse auszuführen, verwendet das Flugzeug die Querruder. Diese erzeugen ein eine Kraft auf die Querruder ($F_a$), das in Kombination mit eine Abstand Schwerpunkt und Querruder ($d_a$) eine ein Von den Querrudern erzeugtes Drehmoment ($T_a$) induziert. Die Querruder befinden sich an den Spitzen der Flügel des Flugzeugs, um ihre die Abstand Schwerpunkt und Querruder ($d_a$) relativ zum Schwerpunkt zu maximieren und eine größere eine Entfernung Schwerpunkt und Aufzüge ($d_e$) zu erreichen.
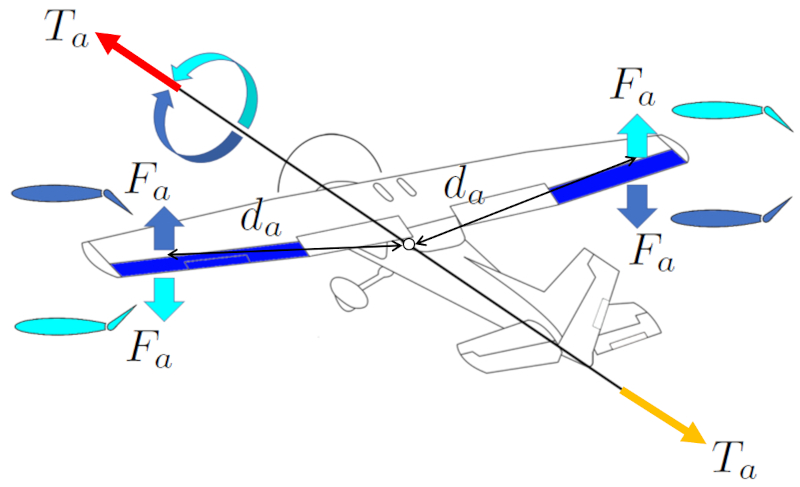
Die Querruder arbeiten asymmetrisch, was bedeutet, dass, wenn das Querruder des rechten Flügels Auftrieb nach oben erzeugt, das Querruder des linken Flügels das Gegenteil tut, und umgekehrt. Auf diese Weise erzeugen diese Kräfte ein Drehmoment, das es dem Flugzeug ermöglicht, im Uhrzeigersinn oder gegen den Uhrzeigersinn zu drehen.
Das Ziel der Rotation besteht darin, mit der Auftriebskraft eine Kraft zu erzeugen, die orthogonal zur zentralen Achse steht und zu einer Kurve im Flugzeug führt. Dies verstärkt die Wirkung des Seitenruders und unterstützt das Drehmanöver des Flugzeugs. Tatsächlich ist dies die Art und Weise, wie Vögel ihre Drehmanöver durchführen, da sie kein Seitenruder haben.
Um das Drehmanöver auszuführen, verwendet der Pilot das Steuerhorn, das eine Art Lenkrad ist und sich in dieselbe Richtung wie das Flugzeug dreht. In anderen Fällen, wie bei den Steuerknüppeln in Airbus-Flugzeugen, gibt es kein Lenkrad, und der Steuerknüppel wird in die gewünschte Richtung geneigt, um die Kurve zu machen.
Eine der Herausforderungen beim Ausführen einer Rotation um die zentrale Achse des Flugzeugs besteht darin, dass die Auftriebskraft verwendet wird, um die Flugbahn abzuweichen, was zu einem Abfall des Auftriebs führt. Das bedeutet, dass das Flugzeug und der Vogel während eines Drehmanövers tendieren, an Höhe zu verlieren, es sei denn, die Leistung wird erhöht.
ID:(15160, 0)
Gierkontrolle
Konzept
Um in einem Flugzeug Kurven zu fliegen, wird das Seitenruder verwendet. Es erzeugt eine eine Kraft am Ruder ($F_r$), die in Kombination mit eine Schwerpunkt und Ruderabstand ($d_r$) eine eine Kraft am Ruder ($F_r$) induziert. Das Seitenruder befindet sich am Heck des Flugzeugs, um eine maximale die Schwerpunkt und Ruderabstand ($d_r$) zu erreichen und eine größere eine Kraft am Ruder ($F_r$) zu erzielen.
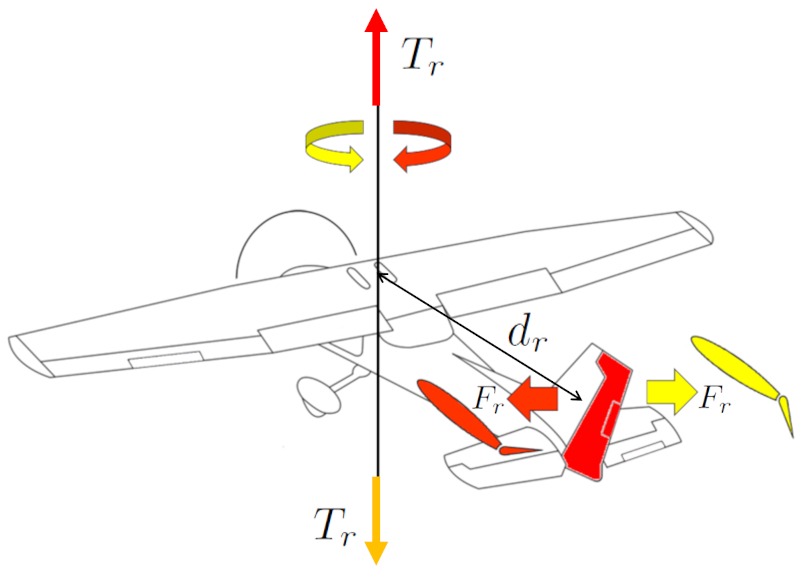
Der Pilot steuert diese Bewegung mithilfe der Pedale. Die Richtung der Kurve wird durch die Ausrichtung der Pedale bestimmt.
ID:(15162, 0)
Auftriebsbeiwert
Gleichung
Aus Messungen geht hervor, dass der Auftriebskoeffizient $C_L$ proportional zum Anstellwinkel $\alpha$ ist:
 $ C_L = c \alpha $ |
Nach einem bestimmten Winkel nimmt die Kurve ab und erreicht schließlich den Wert Null. Dies liegt daran, dass über diesem kritischen Winkel die Wirbel vollständig die obere Fläche des Flügels bedecken und somit der Auftrieb verloren geht. Dieses Phänomen wird als \"Strömungsabriss\" bezeichnet.
ID:(4441, 0)
Auftriebskraft
Gleichung
Um einen höheren Druck unterhalb als oberhalb des Flügels zu erzeugen und Auftrieb zu generieren, wird das Bernoulli-Prinzip angewendet und die fehlende Energieerhaltungsdichte durch ein Koeffizient Fahrstuhl ($C_L$) korrigiert. Der Druck über dem Flügel, die Auftriebskraft ($F_L$), kann unter Verwendung von die Dichte ($\rho$), die Oberfläche, die Auftrieb erzeugt ($S_w$), der Koeffizient Fahrstuhl ($C_L$) und die Geschwindigkeit in Bezug auf das Medium ($v$) mithilfe der folgenden Formel geschätzt werden:
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
Die Auftriebskraft ($F_L$), zusammen mit die Spannweite der Flügel ($L$), die Dichte ($\rho$), der Flügel-Höchstgeschwindigkeitsfaktor ($c_t$), der Flügelbodengeschwindigkeitsfaktor ($c_b$), die Obere Flügellänge ($l_t$), die Länge des unteren Flügels ($l_b$) und die Geschwindigkeit in Bezug auf das Medium ($v$), findet sich in
| $ F_L = \rho L ( c_b l_b - c_t l_t ) v ^2$ |
Wenn wir die Oberfläche, die Auftrieb erzeugt ($S_w$) betrachten, gegeben durch die Spannweite der Flügel ($L$), die Obere Flügellänge ($l_t$) und die Länge des unteren Flügels ($l_b$),
| $ S_w = \displaystyle\frac{1}{2} L ( l_t + l_b )$ |
und für der Koeffizient Fahrstuhl ($C_L$), definiert als
| $ C_L = 4\displaystyle\frac{ c_t l_t - c_b l_b }{ l_t + l_b }$ |
erhalten wir
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
ID:(4417, 0)
Durch das Nicken erzeugte Kraft
Gleichung
| $ T_e = d_e F_e $ |
ID:(15163, 0)
Pitch-Drehmoment
Gleichung
| $ T_e = I_e \alpha_e $ |
ID:(15166, 0)
Kraft, die das Gieren erzeugt
Gleichung
| $ T_r = d_r F_r $ |
ID:(15165, 0)
Gierdrehmoment
Gleichung
| $ T_r = I_r \alpha_r $ |
ID:(15168, 0)
Kraft die das Rollen erzeugt
Gleichung
| $ T_a = d_a F_a $ |
ID:(15164, 0)
Rolldrehmoment
Gleichung
| $ T_a = I_a \alpha_a $ |
ID:(15167, 0)