Vuelo
Storyboard 
Para volar a una altura constante el objeto(avión/ave) debe ajustar el angulo de ataque del ala a la propulsión de modo de contrarrestar el peso y mantener la velocidad deseada.
Variables
Cálculos
Cálculos
Ecuaciones
La fuerza de sustentación ($F_L$), junto con la envergadura de las alas ($L$), la densidad ($\rho$), el factor de velocidad superior del ala ($c_t$), el factor de velocidad inferior del ala ($c_b$), la largo superior del ala ($l_t$), la largo inferior del ala ($l_b$) y la velocidad respecto del medio ($v$), se encuentra en
Si consideramos la superficie que genera sustentación ($S_w$), definido por la envergadura de las alas ($L$), la largo superior del ala ($l_t$) y la largo inferior del ala ($l_b$),
y para el coeficiente de sustentación ($C_L$), definido como
obtenemos
De forma similar a c mo se deriv la ecuaci n para la fuerza de sustentación ($F_L$) utilizando la densidad ($\rho$), el coeficiente de sustentación ($C_L$), la superficie que genera sustentación ($S_w$) y la velocidad respecto del medio ($v$)
en esta analog a, lo que corresponde a la superficie que genera sustentación ($S_w$) ser equivalente a el perfil total del objeto ($S_p$) y el coeficiente de sustentación ($C_L$) a el coeficiente de resistencia ($C_W$), con lo que se calcula la fuerza de resistencia ($F_W$):
El coeficiente de resistencia se mide y, en flujos turbulentos sobre cuerpos aerodin micos, generalmente se registran valores alrededor de 0.4.
Utilizando las relaciones de la fuerza total de resistencia ($F_R$) con la fuerza de sustentación ($F_L$), la fuerza de resistencia ($F_W$) y el angulo de ataque del ala ($\alpha$):
podemos calcular la fuerza de resistencia utilizando la densidad ($\rho$), el coeficiente de resistencia ($C_W$), el perfil total del objeto ($S_p$) y la velocidad respecto del medio ($v$):
y la fuerza de sustentaci n con la superficie que genera sustentación ($S_w$) y el coeficiente de sustentación ($C_L$):
utilizando la relaci n para el coeficiente de sustentación ($C_L$) con la constante de proporcionalidad del coeficiente de sustentación ($c$):
usando la relaci n para el seno del ngulo de ataque $\alpha$ peque o:
y el coseno:
con la condici n de equilibrar el peso del ave o avi n para la masa del cuerpo ($m$) y la aceleración gravitacional ($g$):
obtenemos:
La potencia en vuelo ($P$) en el tiempo de despegue ($t$) seg n la ecuaci n:
Dado que la variaci n de la energía del objeto volando ($E$) es igual a la fuerza total de resistencia ($F_R$) multiplicada por la variaci n el camino recorrido ($s$), tenemos:
De esta manera, obtenemos:
$P=\displaystyle\frac{dE}{dt}= F_R \displaystyle\frac{ds}{dt}$
Sin embargo, dado que la distancia recorrida en un intervalo de tiempo es la velocidad respecto del medio ($v$):
Finalmente, podemos escribir la expresi n de la potencia como:
La fuerza total de resistencia ($F_R$) est relacionado con la densidad ($\rho$), la superficie que genera sustentación ($S_w$), el perfil total del objeto ($S_p$), el coeficiente de resistencia ($C_W$), la constante de proporcionalidad del coeficiente de sustentación ($c$), la masa del cuerpo ($m$) y la aceleración gravitacional ($g$) seg n la ecuaci n
entonces, utilizando la ecuaci n para la potencia en vuelo ($P$)
obtenemos:
La componente horizontal de la fuerza de sustentación ($F_L$) corresponde a la fuerza de sustentación ($F_L$) multiplicada por el seno del ERROR:6121,0:
$F_L \sin\alpha $
y la componente horizontal de la fuerza de resistencia ($F_W$) corresponde a la fuerza de resistencia ($F_W$) multiplicada por el coseno del ngulo de ERROR:6121,0:
$F_W \cos\alpha $
Por lo tanto, la fuerza total de resistencia ($F_R$) se calcula como:
Ejemplos
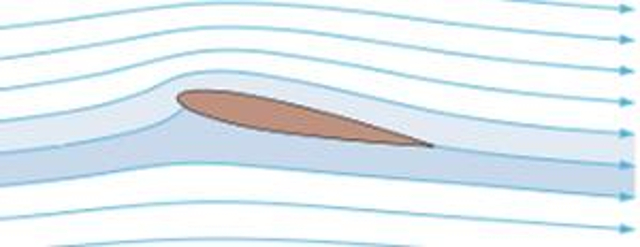
Si asumimos que el flujo alrededor de un ala es laminar, podemos observar m ltiples capas que rodean el ala. Aquellas en la parte superior son un poco m s largas debido a la curvatura hacia arriba, mientras que las capas inferiores tienden a ser m s cortas y, por lo tanto, m s cercanas al ala.
Si suponemos que el flujo es tal que estas capas convergen de manera que puntos cercanos separados por el ala vuelven a estar en la misma posici n relativa una vez que termina la bifurcaci n, entonces la velocidad de las capas superiores ser necesariamente mayor que la de las capas inferiores. Es importante tener en cuenta que esta es solo una suposici n y no existe una necesidad real de que converjan; de hecho, podr an terminar desfasadas sin ning n problema.
Dado que la velocidad en las capas superiores del ala es mayor que en las inferiores, esto implica que la presi n en la parte superior del ala es menor que en la parte inferior.
Este fen meno significa que, en efecto, existe una fuerza mayor desde abajo del ala que act a sobre el ala, lo que da lugar a una fuerza de sustentaci n.
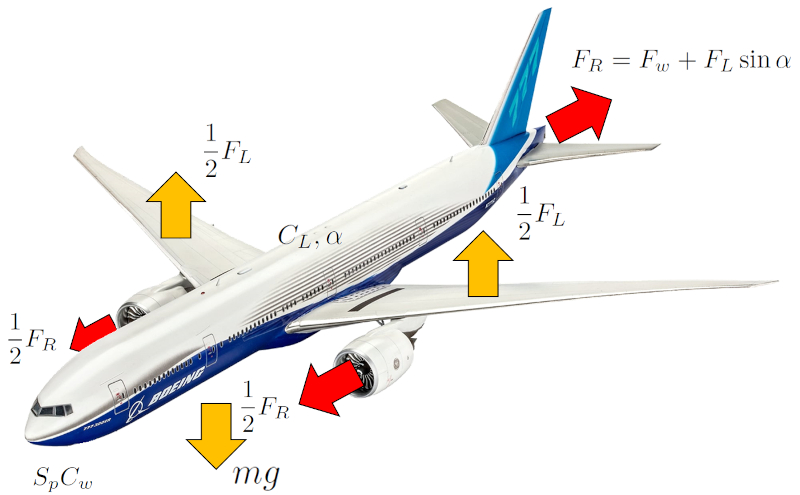
Las fuerzas que influyen en la aeronave o el ave se dividen en dos categor as fundamentales:
Fuerzas que afectan el control del movimiento del centro de masa:
• la fuerza de sustentación ($F_L$), que contrarresta a la fuerza gravitacional ($F_g$).
• la fuerza de propulsión ($F_p$), que se opone a la fuerza de resistencia ($F_W$).
Fuerzas para lograr la rotaci n de la aeronave o el ave alrededor del centro de masa, que se alcanzan mediante los alerones en las alas y el tim n:
• Los alerones permiten generar un momento de giro al modificar de forma asim trica la sustentaci n en cada ala.
• El tim n controla la direcci n de la aeronave o el ave al desviar el flujo de aire.
Los par metros clave para controlar el movimiento del centro de masa son:
• la superficie que genera sustentación ($S_w$) y el perfil total del objeto ($S_p$).
• el coeficiente de sustentación ($C_L$) y el coeficiente de resistencia ($C_W$), siendo esta ltima dependiente de el angulo de ataque del ala ($\alpha$).
La fuerza gravitacional ($F_g$) se basa en la masa gravitacional ($m_g$) del objeto y en una constante que refleja la intensidad de la gravedad en la superficie del planeta. Esta ltima es identificada por la aceleración gravitacional ($g$), que es igual a $9.8 m/s^2$.
En consecuencia, se concluye que:
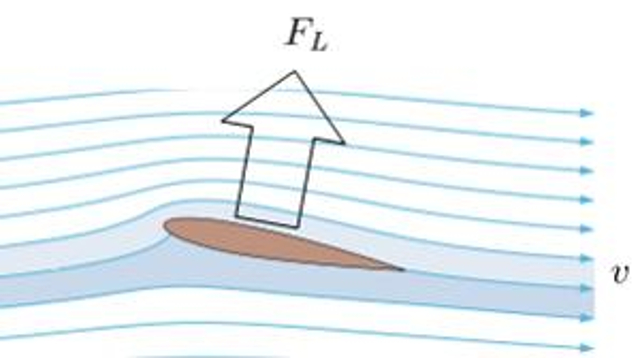
Para crear una presi n mayor debajo que encima del ala y generar sustentaci n, se emplea la Ley de Bernoulli, corrigiendo la falta de conservaci n de la densidad de energ a mediante un coeficiente de sustentación ($C_L$). La presi n sobre el ala, la fuerza de sustentación ($F_L$), se puede estimar utilizando la densidad ($\rho$), la superficie que genera sustentación ($S_w$), el coeficiente de sustentación ($C_L$) y la velocidad respecto del medio ($v$) mediante la siguiente f rmula:
Para calcular la fuerza total de resistencia ($F_R$), suponemos ngulos peque os y consideramos una situaci n en la que el ngulo permite mantener la masa del cuerpo ($m$). Utilizando esta aproximaci n y las variables el coeficiente de sustentación ($C_L$), el coeficiente de resistencia ($C_W$), la superficie que genera sustentación ($S_w$), el perfil total del objeto ($S_p$), la aceleración gravitacional ($g$), la constante de proporcionalidad del coeficiente de sustentación ($c$), la densidad ($\rho$) y la velocidad respecto del medio ($v$), obtenemos la siguiente expresi n:
La fuerza total de resistencia ($F_R$) se compone de las componentes horizontales de la fuerza de resistencia ($F_W$) y de la fuerza de sustentación ($F_L$), que se puede calcular a partir del ERROR:6121,0:
La fuerza de resistencia ($F_W$) se puede calcular utilizando la densidad ($\rho$), el coeficiente de resistencia ($C_W$), el perfil total del objeto ($S_p$) y la velocidad respecto del medio ($v$) de acuerdo con la siguiente f rmula:
La potencia en vuelo ($P$) es la energ a por unidad de tiempo que se necesita suministrar para mantener una la fuerza total de resistencia ($F_R$) dada. Por lo tanto, se puede calcular en funci n de dicha fuerza multiplic ndola por la velocidad respecto del medio ($v$):
Para obtener la potencia en vuelo ($P$), es necesario multiplicar la fuerza total de resistencia ($F_R$) por la velocidad respecto del medio ($v$). Dado que la fuerza total de resistencia ($F_R$) es una funci n de la densidad ($\rho$), la superficie que genera sustentación ($S_w$), el perfil total del objeto ($S_p$), el coeficiente de resistencia ($C_W$), la constante de proporcionalidad del coeficiente de sustentación ($c$), la masa del cuerpo ($m$) y la aceleración gravitacional ($g$), que es igual a
el potencial es
ID:(1463, 0)