Flight
Storyboard 
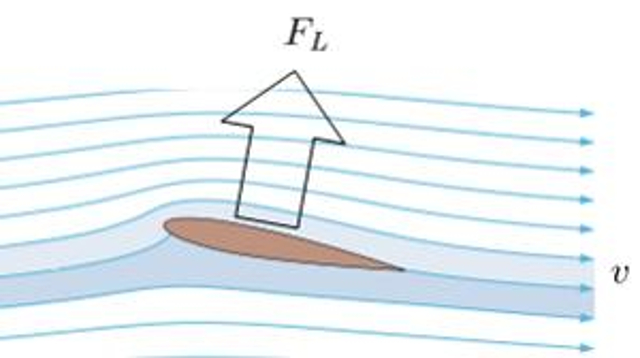
To fly at a constant height the object (airplane / bird) must adjust the angle of attack of the wing to the propulsion so as to counteract the weight and maintain the desired speed.
Variables
Calculations
Calculations
Equations
The lift force ($F_L$), along with the wing span ($L$), the density ($\rho$), the wing top speed factor ($c_t$), the wing bottom speed factor ($c_b$), the upper wing length ($l_t$), the bottom wing length ($l_b$), and the speed with respect to the medium ($v$), is found in
If we consider the surface that generates lift ($S_w$), given by the wing span ($L$), the upper wing length ($l_t$), and the bottom wing length ($l_b$),
and for the coefficient of lift ($C_L$), defined as
we obtain
Similarly to how the equation for the lift force ($F_L$) was derived using the density ($\rho$), the coefficient of lift ($C_L$), the surface that generates lift ($S_w$), and the speed with respect to the medium ($v$)
in this analogy, what corresponds to the surface that generates lift ($S_w$) will be equivalent to the total object profile ($S_p$) and the coefficient of lift ($C_L$) to the coefficient of resistance ($C_W$), thus the resistance force ($F_W$) is calculated:
The drag coefficient is measured and, in turbulent flows over aerodynamic bodies, values are generally found around 0.4.
Using the relationships of the total resistance force ($F_R$) with the lift force ($F_L$), the resistance force ($F_W$), and the angle of attack of a wing ($\alpha$):
we can calculate using the resistance force with the density ($\rho$), the coefficient of resistance ($C_W$), the total object profile ($S_p$), and the speed with respect to the medium ($v$):
and the lift force with the surface that generates lift ($S_w$) and the coefficient of lift ($C_L$):
using the relationship for the coefficient of lift ($C_L$) with the proportionality constant coefficient sustainability ($c$):
using the relationship for the sine of the small angle of attack $\alpha$:
and the cosine:
with the condition to balance the weight of the bird or aircraft for the body mass ($m$) and the gravitational Acceleration ($g$):
we obtain:
The power is defined as the energy $\Delta W$ per time $\Delta t$ according to the equation:
Since energy is equal to force $F$ multiplied by the distance traveled $\Delta s$, we have:
Thus, we obtain:
$P=\displaystyle\frac{\Delta W}{\Delta t}= F_R \displaystyle\frac{\Delta s}{\Delta t}$
However, since the distance traveled in a time interval is the velocity $v$:
Finally, we can write the expression for power as:
The total resistance force ($F_R$) is a function of the density ($\rho$), the surface that generates lift ($S_w$), the total object profile ($S_p$), the coefficient of resistance ($C_W$), the proportionality constant coefficient sustainability ($c$), the body mass ($m$), and the gravitational Acceleration ($g$), which is equal to
therefore, using the equation for the power of flight ($P$)
we obtain:
The horizontal component of the lift force corresponds to the force $F_L$ multiplied by the sine of the angle of attack $\alpha$:
$F_L \sin\alpha $
And the horizontal component of the drag force corresponds to the force $F_W$ multiplied by the cosine of the angle of attack $\alpha$:
$F_W \cos\alpha $
Therefore, the total resistance force can be calculated as:
Examples
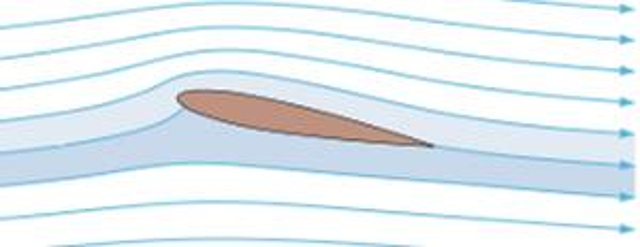
If we assume that the flow around a wing is laminar, we can observe multiple layers surrounding the wing. Those on the upper side tend to be slightly longer due to the upward curvature, while the lower layers tend to be shorter and, therefore, closer to the wing.
Supposing that the flow is such that these layers converge in a way that points close together on either side of the wing return to the same relative position once the flow separates, the speed of the upper layers will necessarily be higher than that of the lower layers. It's important to keep in mind that this is just an assumption, and there is no real necessity for them to converge; in fact, they could end up being out of phase without any issues.
Since the velocity in the upper layers of the wing is greater than in the lower layers, this implies that the pressure on the upper surface of the wing is lower than on the lower surface.
This effectively means that there is a greater force from below the wing compared to above the wing, which leads to the generation of lift force.
The forces that influence an aircraft or bird can be categorized into two fundamental groups:
Forces that impact the control of the center of mass's movement:
• the lift force ($F_L$), which counteracts the gravitational force ($F_g$).
• the propulsion force ($F_p$), which opposes the resistance force ($F_W$).
Forces aimed at achieving the rotation of the aircraft or bird around the center of mass, achieved through the ailerons on the wings and the rudder:
• Ailerons allow the generation of a turning moment by asymmetrically altering lift on each wing.
• The rudder controls the direction of the aircraft or bird by redirecting the airflow.
Key parameters for controlling the center of mass's movement are:
• the surface that generates lift ($S_w$) and the total object profile ($S_p$).
• the coefficient of lift ($C_L$) and the coefficient of resistance ($C_W$), the latter being dependent on the angle of attack of a wing ($\alpha$).
The gravitational Force ($F_g$) is based on the gravitational mass ($m_g$) of the object and on a constant reflecting the intensity of gravity at the planet's surface. The latter is identified by the gravitational Acceleration ($g$), which is equal to $9.8 m/s^2$.
Consequently, it is concluded that:
To generate higher pressure below than above the wing and generate lift, Bernoulli's principle is employed, correcting for the lack of energy density conservation using ERROR:6119.1. The pressure over the wing, the lift force ($F_L$), can be estimated using the density ($\rho$), the surface that generates lift ($S_w$), the coefficient of lift ($C_L$), and the speed with respect to the medium ($v$) through the following formula:
To calculate the total resistance force ($F_R$), we assume small angles and consider a situation where the angle is such that it maintains the body mass ($m$). Using this approximation and the variables the coefficient of lift ($C_L$), the coefficient of resistance ($C_W$), the surface that generates lift ($S_w$), the total object profile ($S_p$), the gravitational Acceleration ($g$), the proportionality constant coefficient sustainability ($c$), the density ($\rho$), and the speed with respect to the medium ($v$), we obtain the following expression:
The total force of resistance is composed of the horizontal components of the wing profile's resistance force $F_W$ and the lift force $F_L$, which can be calculated from the angle of attack $\alpha$:
The resistance force ($F_W$) kann mit the density ($\rho$), the coefficient of resistance ($C_W$), the total object profile ($S_p$) und the speed with respect to the medium ($v$) entsprechend berechnet werden folgende Formel:
Power $P$ is the energy per unit of time that needs to be supplied to sustain a given force $F_R$. Therefore, it can be calculated based on the force by multiplying it by the velocity $v$:
To obtain the power of flight ($P$), you need to multiply the total resistance force ($F_R$) by the speed with respect to the medium ($v$). Since the total resistance force ($F_R$) is a function of the density ($\rho$), the surface that generates lift ($S_w$), the total object profile ($S_p$), the coefficient of resistance ($C_W$), the proportionality constant coefficient sustainability ($c$), the body mass ($m$), and the gravitational Acceleration ($g$), which is equal to
the potential is
ID:(1463, 0)