Vol
Storyboard 
Pour voler à une altitude constante, l'objet (avion/oiseau) doit ajuster l'angle d'attaque de l'aile de manière à contrer le poids avec la poussée et maintenir la vitesse souhaitée.
Variables
Calculs
Calculs
Équations
A force de levage ($F_L$), en compagnie de a envergure des ailes ($L$), a densité ($\rho$), le facteur de vitesse maximale de l'aile ($c_t$), le facteur de vitesse en bas d'aile ($c_b$), a longueur de l'aile supérieure ($l_t$), a longueur de l'aile inférieure ($l_b$) et a vitesse par rapport au milieu ($v$), se trouve dans
Si nous consid rons a surface génératrice de portance ($S_w$), d fini par a envergure des ailes ($L$), a longueur de l'aile supérieure ($l_t$) et a longueur de l'aile inférieure ($l_b$),
et pour le coefficient de portance ($C_L$), d fini comme
nous obtenons
De mani re similaire la fa on dont l' quation pour a force de levage ($F_L$) a t d riv e en utilisant a densité ($\rho$), le coefficient de portance ($C_L$), a surface génératrice de portance ($S_w$) et a vitesse par rapport au milieu ($v$)
dans cette analogie, ce qui correspond a surface génératrice de portance ($S_w$) sera quivalent le profil total de l'objet ($S_p$) et le coefficient de portance ($C_L$) Le coefficient de résistance ($C_W$), ce qui permet de calculer a force de résistance ($F_W$) :
Le coefficient de tra n e est mesur et, dans les coulements turbulents sur les corps a rodynamiques, les valeurs sont g n ralement autour de 0.4.
En utilisant les relations de a force de résistance totale ($F_R$) avec a force de levage ($F_L$), a force de résistance ($F_W$), et le accélération maximale ($\alpha$) :
nous pouvons calculer en utilisant la force de r sistance avec a densité ($\rho$), le coefficient de résistance ($C_W$), le profil total de l'objet ($S_p$), et a vitesse par rapport au milieu ($v$) :
et la force de portance avec a surface génératrice de portance ($S_w$) et le coefficient de portance ($C_L$) :
en utilisant la relation pour le coefficient de portance ($C_L$) avec a constante de proportionnalité du coefficient de portance ($c$) :
en utilisant la relation pour le sinus du petit angle d'attaque $\alpha$ :
et le cosinus :
avec la condition d' quilibrer le poids de l'oiseau ou de l'a ronef pour a masse corporelle ($m$) et a accélération gravitationnelle ($g$) :
nous obtenons :
La puissance est d finie comme l' nergie $\Delta W$ par temps $\Delta t$, selon l\' quation:
Puisque l\' nergie est gale la force $F$ multipli e par la distance parcourue $\Delta s$, nous avons:
Ainsi, on obtient :
$P=\displaystyle\frac{\Delta W}{\Delta t}= F_R \displaystyle\frac{\Delta s}{\Delta t}$
Cependant, puisque la distance parcourue dans un intervalle de temps est la vitesse $v$:
Enfin, nous pouvons crire l\'expression de la puissance comme:
A force de résistance totale ($F_R$) d pend de a densité ($\rho$), a surface génératrice de portance ($S_w$), le profil total de l'objet ($S_p$), le coefficient de résistance ($C_W$), a constante de proportionnalité du coefficient de portance ($c$), a masse corporelle ($m$) et a accélération gravitationnelle ($g$), ce qui est gal
par cons quent, en utilisant l' quation pour a profil total de l'objet ($P$)
nous obtenons :
La composante horizontale de la force de sustentation correspond la force $F_L$ multipli e par le sinus de l'angle d'attaque $\alpha$:
$F_L \sin\alpha $
et la composante horizontale de la force de r sistance correspond la force $F_W$ multipli e par le cosinus de l\'angle d\'attaque $\alpha$:
$F_W \cos\alpha $
Par cons quent, la force totale de r sistance se calcule de la mani re suivante :
Exemples
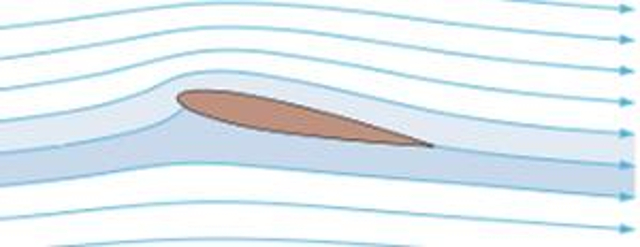
Si l'on suppose que l' coulement autour d'une aile est laminaire, nous pouvons observer plusieurs couches entourant l'aile. Celles situ es sur le dessus sont g n ralement un peu plus longues en raison de la courbure vers le haut, tandis que les couches inf rieures ont tendance tre plus courtes et donc plus proches de l'aile.
En supposant que l' coulement soit tel que ces couches convergent de mani re ce que des points proches de chaque c t de l'aile reviennent la m me position relative une fois que l' coulement se s pare, la vitesse des couches sup rieures sera n cessairement plus lev e que celle des couches inf rieures. Il est important de noter que ceci n'est qu'une hypoth se, et il n'y a aucune r elle n cessit pour qu'elles convergent; en fait, elles pourraient tr s bien tre d phas es sans aucun probl me.
tant donn que la vitesse dans les couches sup rieures de l'aile est plus lev e que dans les couches inf rieures, cela signifie que la pression sur la surface sup rieure de l'aile est inf rieure celle sur la surface inf rieure.
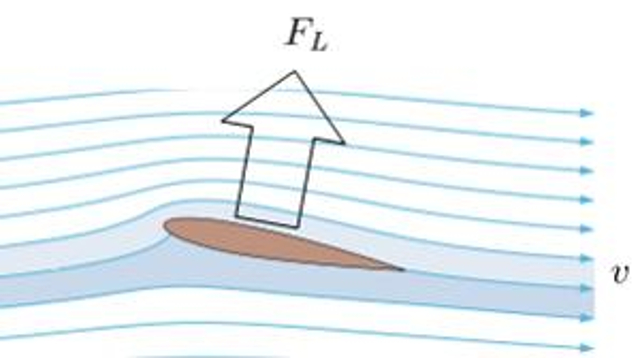
Cela signifie effectivement qu'il existe une force plus importante agissant depuis le dessous de l'aile par rapport au dessus de l'aile, ce qui conduit la g n ration d'une force de portance.
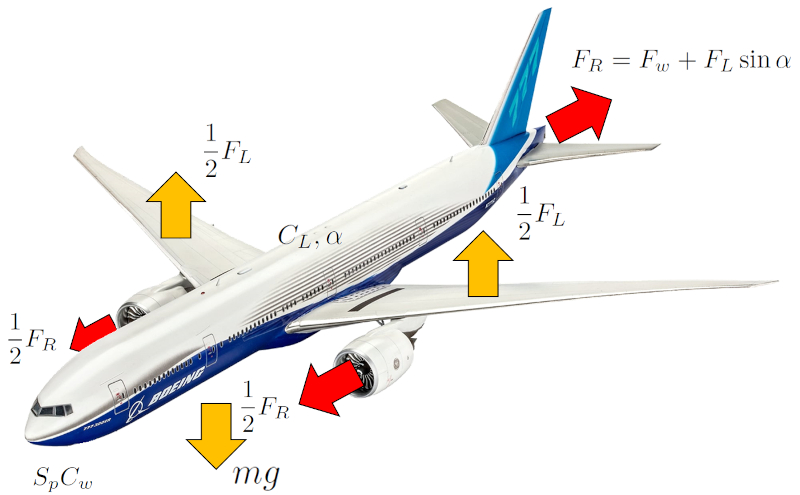
Les forces qui influencent un avion ou un oiseau peuvent tre class es en deux cat gories fondamentales :
Forces qui affectent le contr le du mouvement du centre de masse :
• a force de levage ($F_L$), qui s'oppose a force gravitationnelle ($F_g$).
• a force de propulsion ($F_p$), qui s'oppose a force de résistance ($F_W$).
Forces visant obtenir la rotation de l'avion ou de l'oiseau autour du centre de masse, obtenues gr ce aux ailerons sur les ailes et au gouvernail de direction :
• Les ailerons permettent de g n rer un moment de torsion en modifiant de mani re asym trique la portance sur chaque aile.
• Le gouvernail de direction contr le la direction de l'avion ou de l'oiseau en redirigeant le flux d'air.
Les param tres cl s pour contr ler le mouvement du centre de masse sont :
• a surface génératrice de portance ($S_w$) et le profil total de l'objet ($S_p$).
• le coefficient de portance ($C_L$) et le coefficient de résistance ($C_W$), ce dernier d pendant de le accélération maximale ($\alpha$).
A force gravitationnelle ($F_g$) est bas sur a masse gravitationnelle ($m_g$) de l'objet et sur une constante qui refl te l'intensit de la gravit la surface de la plan te. Cette derni re est identifi e par a accélération gravitationnelle ($g$), qui est gal $9.8 m/s^2$.
Par cons quent, on en conclut que :
Pour g n rer une pression plus lev e en dessous qu'au-dessus de l'aile et produire de la portance, le principe de Bernoulli est utilis pour corriger le manque de conservation de la densit d' nergie avec un coefficient de portance ($C_L$). La pression sur l'aile, a force de levage ($F_L$), peut tre estim e en utilisant a densité ($\rho$), a surface génératrice de portance ($S_w$), le coefficient de portance ($C_L$), et a vitesse par rapport au milieu ($v$) gr ce la formule suivante :
Pour calculer a force de résistance totale ($F_R$), nous supposons de petits angles et consid rons une situation o l'angle est tel qu'il maintient a masse corporelle ($m$). En utilisant cette approximation et les variables le coefficient de portance ($C_L$), le coefficient de résistance ($C_W$), a surface génératrice de portance ($S_w$), le profil total de l'objet ($S_p$), a accélération gravitationnelle ($g$), a constante de proportionnalité du coefficient de portance ($c$), a densité ($\rho$) et a vitesse par rapport au milieu ($v$), nous obtenons l'expression suivante :
La force totale de r sistance est compos e des composantes horizontales de la force de r sistance du profil de l'aile $F_W$ et de la force de portance $F_L$, qui peuvent tre calcul es partir de l'angle d\'attaque $\alpha$:
A force de résistance ($F_W$) peut tre calcul en utilisant a densité ($\rho$), le coefficient de résistance ($C_W$), le profil total de l'objet ($S_p$) et a vitesse par rapport au milieu ($v$) selon le formule suivante :
La puissance $P$ est l' nergie par unit de temps qui doit tre fournie pour maintenir une force $F_R$ donn e. Par cons quent, elle peut tre calcul e en fonction de cette force en la multipliant par la vitesse $v$:
Pour obtenir a profil total de l'objet ($P$), il est n cessaire de multiplier a force de résistance totale ($F_R$) par a vitesse par rapport au milieu ($v$). Puisque a force de résistance totale ($F_R$) est une fonction de a densité ($\rho$), a surface génératrice de portance ($S_w$), le profil total de l'objet ($S_p$), le coefficient de résistance ($C_W$), a constante de proportionnalité du coefficient de portance ($c$), a masse corporelle ($m$) et a accélération gravitationnelle ($g$), qui est gale
le potentiel est
ID:(1463, 0)