Controle, uso do elevador
Imagem 
Os ailerons são partes das asas que permitem curvar a sua extremidade para cima (gerando força para baixo) ou para baixo (gerando força para cima). Todos eles estão posicionados em pontos afastados do centro de massa para alcançar uma maior distância e, assim, um maior torque, tornando-os mais eficientes na rotação.
Devido à geometria, existem três eixos ao redor dos quais a aeronave gira. O aileron do leme gera uma rotação em torno de um eixo vertical. Os ailerons nas asas traseiras menores (conhecidos como estabilizadores) permitem uma rotação em torno de um eixo perpendicular ao eixo da aeronave, permitindo levantar e baixar o nariz da aeronave. Por fim, existem os ailerons nas asas principais que permitem que a aeronave gire em torno de seu eixo central.
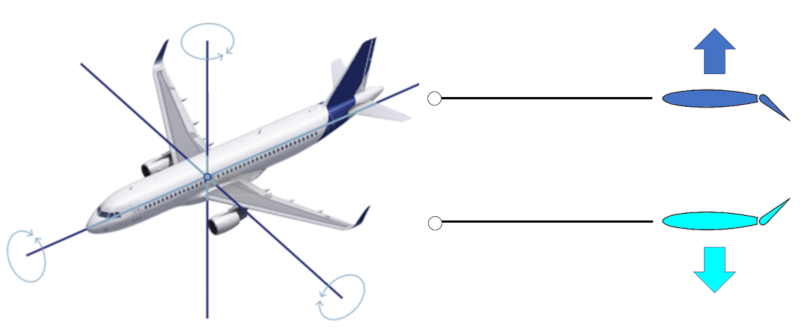
Existe um tipo de aileron que, adicionalmente, é extensível nas asas principais, próximo ao corpo da aeronave, conhecido como flaps, que permitem aumentar/reduzir tanto a área da asa quanto o ângulo de ataque.
Por último, existem superfícies que podem ser elevadas para perturbar o fluxo de ar sobre a asa e são usadas para frenagem, conhecidas como spoilers.
ID:(11081, 0)
Controle de tom
Nota 
Para inclinar o nariz da aeronave para cima ou para baixo, são utilizados os elevadores. Ambos são empregados de forma simétrica para gerar um efeito la força nos elevadores ($F_e$) simétrico. Colocando-os na cauda da aeronave, alcança-se uma ERROR:10215.1 maior eficácia ao posicioná-los próximo ao centro de massa. Isso proporciona controle suficiente para elevar ou baixar o nariz da aeronave.
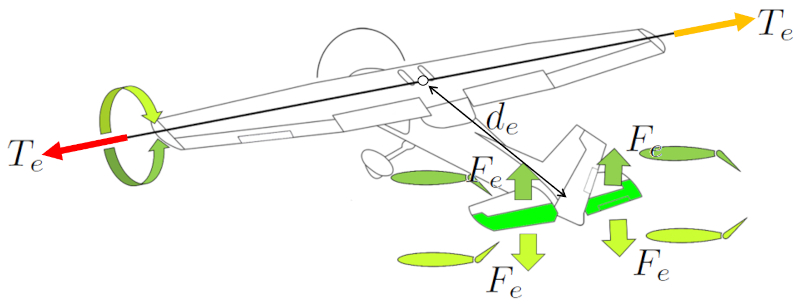
Em aeronaves mais antigas, o controle dos ailerons traseiros é realizado através de um manche, onde empurrar para a frente faz o nariz da aeronave descer, e puxar para trás eleva o nariz. Nas aeronaves da família Airbus, esse controle é feito com um joystick.
No caso das aves, existe uma solução semelhante, embora neste caso, a cauda não seja interrompida por um leme.
ID:(15161, 0)
Controle de rolagem
Exercício 
Para realizar um rolamento em torno do seu eixo, a aeronave utiliza os ailerons. Estes geram uma força nos ailerons ($F_a$) que, em conjunto com uma centro de distância de massa e ailerons ($d_a$), induzem um torque gerado pelos ailerons ($T_a$). Os ailerons estão localizados nas pontas das asas da aeronave para maximizar sua la centro de distância de massa e ailerons ($d_a$) em relação ao centro de massa e obter uma maior uma centro de distância de massa e elevadores ($d_e$).
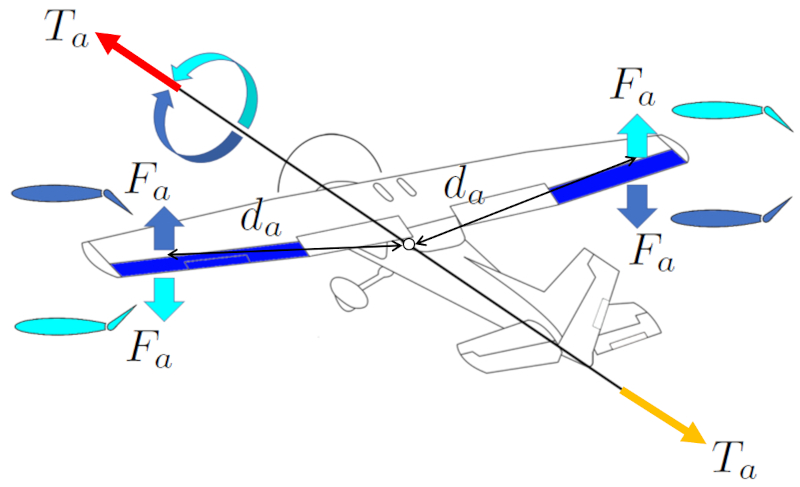
Os ailerons operam de maneira assimétrica, o que significa que se o aileron da asa direita gera sustentação para cima, o da asa esquerda faz o oposto, e vice-versa. Dessa forma, essas forças geram um torque que permite girar no sentido horário ou anti-horário.
O objetivo da rotação é gerar, com a força de sustentação, uma força ortogonal ao eixo central, resultando em uma curva na aeronave. Isso reforça a ação do leme, auxiliando na manobra de viragem da aeronave. De fato, essa é a forma como as aves realizam suas manobras de viragem, já que não possuem um leme.
Para realizar a manobra de viragem, o piloto utiliza o controle de coluna, que possui um volante que gira na mesma direção que a aeronave. Em outros casos, como no joystick das aeronaves Airbus, não há um volante, e o joystick é inclinado na direção desejada para realizar a curva.
Um dos problemas que surgem ao realizar uma rotação em torno do eixo central da aeronave é que a força de sustentação é utilizada para desviar a trajetória, resultando em uma diminuição da sustentação. Isso significa que, durante uma manobra de viragem, a aeronave e a ave tendem a perder altitude a menos que a potência seja aumentada.
ID:(15160, 0)
Controle de guinada
Script 
Para realizar curvas em uma aeronave, utiliza-se o leme de direção. Ele gera uma uma la force à la barre ($F_r$), que, combinada com uma centro de massa e distância do leme ($d_r$), induz uma uma la force à la barre ($F_r$). O leme de direção está localizado na cauda da aeronave para maximizar uma la centro de massa e distância do leme ($d_r$) e alcançar um maior uma la force à la barre ($F_r$).
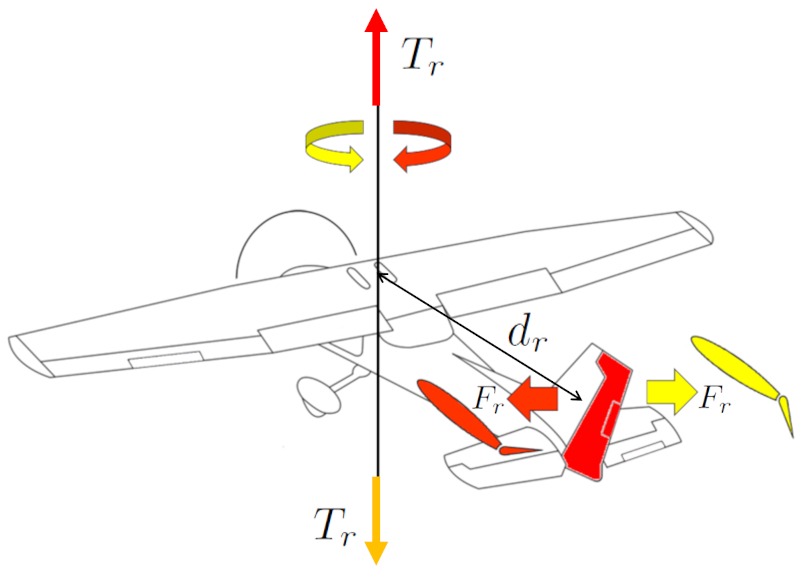
O piloto controla esse movimento utilizando os pedais. A direção da curva é determinada pela direção dos pedais.
ID:(15162, 0)



