Contrôle
Storyboard 
Pour manuvrer l'aéronef, les gouvernes de profondeur, les ailerons et le gouvernail sont utilisés. Ils exploitent tous la portance générée par le profil de l'aile pour créer des forces à des points éloignés du centre de masse, induisant ainsi des couples qui font tourner l'aéronef.
ID:(2055, 0)
Contrôle, utilisation de l'ascenseur
Image 
Les ailerons sont des parties des ailes qui permettent de courber leur extrémité vers le haut (générant une force vers le bas) ou vers le bas (générant une force vers le haut). Ils sont tous situés à des points éloignés du centre de masse pour obtenir une plus grande distance et ainsi un couple plus élevé, ce qui les rend plus efficaces lors de la rotation.
En raison de la géométrie, il existe trois axes autour desquels l'avion tourne. L'aileron de direction génère une rotation autour d\'un axe vertical. Les ailerons des petites ailes arrière (appelés stabilisateurs) permettent une rotation autour d\'un axe perpendiculaire à l\'axe de l\'avion pour lever et abaisser le nez de celui-ci. Enfin, il y a les ailerons des ailes qui permettent à l\'avion de tourner autour de son axe central.
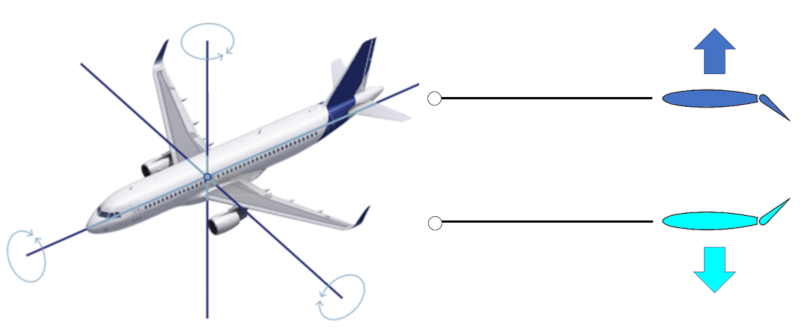
Il existe un type d\'ailerons, appelés volets, qui sont également extensibles sur les ailes principales près du fuselage, ce qui permet d\'augmenter/réduire à la fois la surface de l\'aile et l\'angle d\'attaque.
Enfin, il existe des surfaces qui peuvent être relevées pour perturber le flux d\'air sur l\'aile, utilisées pour freiner, et qui sont appelées spoilers.
ID:(11081, 0)
Contrôle du pas
Noter 
Pour incliner le nez de l'avion vers le haut ou vers le bas, on utilise les élévateurs. Les deux élévateurs sont utilisés de manière symétrique pour générer un effet symétrique a la force des ascenseurs ($F_e$). En les plaçant à l'arrière de l'avion, on obtient une ERROR:10215.1 plus grande efficacité en les situant près du centre de masse. Cela offre un contrôle suffisant pour relever ou abaisser le nez de l'avion.
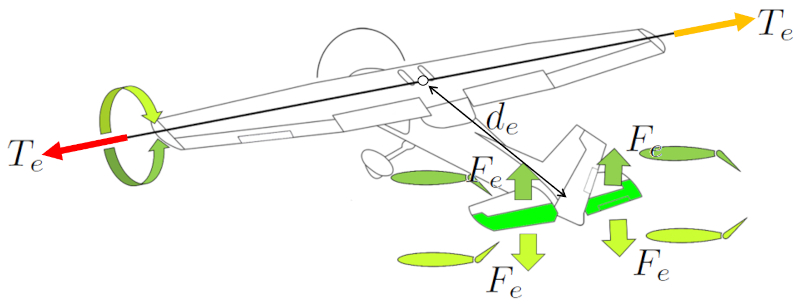
Sur les avions plus anciens, le contrôle des ailerons arrière s'effectue à l'aide d'un manche, où pousser vers l'avant fait descendre le nez de l'avion, et tirer vers l'arrière relève le nez. Sur les avions de la famille Airbus, ce contrôle s'effectue à l'aide d'un joystick.
Dans le cas des oiseaux, une solution similaire existe, bien que dans ce cas, la queue ne soit pas interrompue par un gouvernail.
ID:(15161, 0)
Contrôle du roulis
Exercer 
Pour effectuer un roulis autour de son axe, l'aéronef utilise les ailerons. Ils génèrent une une forcer sur les ailerons ($F_a$) qui, combinée à Une distance centre de masse et ailerons ($d_a$), induit une un couple généré par les ailerons ($T_a$). Les ailerons sont situés aux extrémités des ailes de l'aéronef pour maximiser leur a distance centre de masse et ailerons ($d_a$) par rapport au centre de masse et obtenir une plus grande une distance centre de masse et ascenseurs ($d_e$).
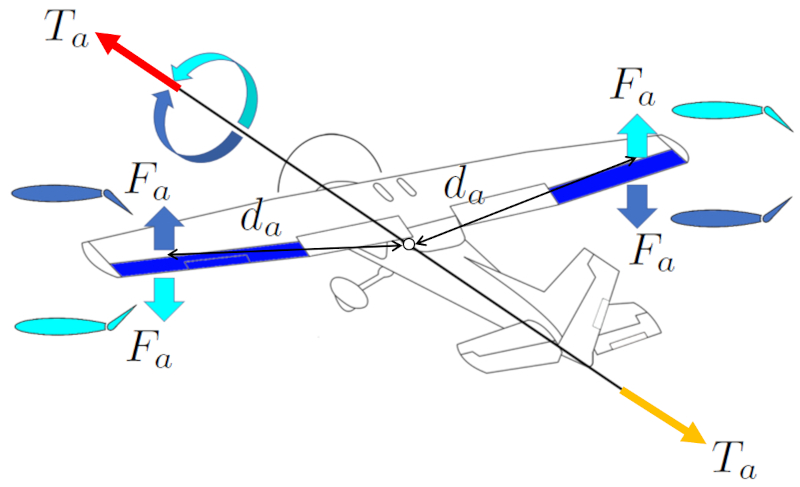
Les ailerons fonctionnent de manière asymétrique, ce qui signifie que si l'aileron de l'aile droite génère une portance vers le haut, celui de l'aile gauche fait le contraire, et vice versa. De cette manière, ces forces génèrent un couple qui permet de tourner dans le sens des aiguilles d'une montre ou dans le sens contraire.
L'objectif de la rotation est de générer, avec la force de portance, une force orthogonale à l'axe central, ce qui entraîne une courbe dans l'aéronef. Cela renforce l'action du gouvernail, aidant ainsi à la manuvre de virage de l'aéronef. En fait, c'est ainsi que les oiseaux réalisent leurs manuvres de virage, car ils ne possèdent pas de gouvernail.
Pour effectuer la manuvre de virage, le pilote utilise le contrôle de colonne, qui comporte un volant qui tourne dans la même direction que l'aéronef. Dans d'autres cas, comme avec le joystick des avions Airbus, il n'y a pas de volant, et le joystick est incliné dans la direction souhaitée pour effectuer la courbe.
Un des problèmes qui surviennent lors de la réalisation d'une rotation autour de l'axe central de l'aéronef est que la force de portance est utilisée pour dévier la trajectoire, ce qui entraîne une diminution de la portance. Cela signifie que, lors d'une manuvre de virage, l'aéronef et l'oiseau ont tendance à perdre de l'altitude à moins que la puissance ne soit augmentée.
ID:(15160, 0)
Contrôle du lacet
Script 
Pour effectuer des virages dans une aéronef, on utilise le gouvernail de direction. Il génère une une força no comando ($F_r$), qui, combinée à Une centre de masse et distance du gouvernail ($d_r$), induit une une força no comando ($F_r$). Le gouvernail de direction est situé à l'arrière de l'aéronef pour maximiser une a centre de masse et distance du gouvernail ($d_r$) et obtenir une plus grande une força no comando ($F_r$).
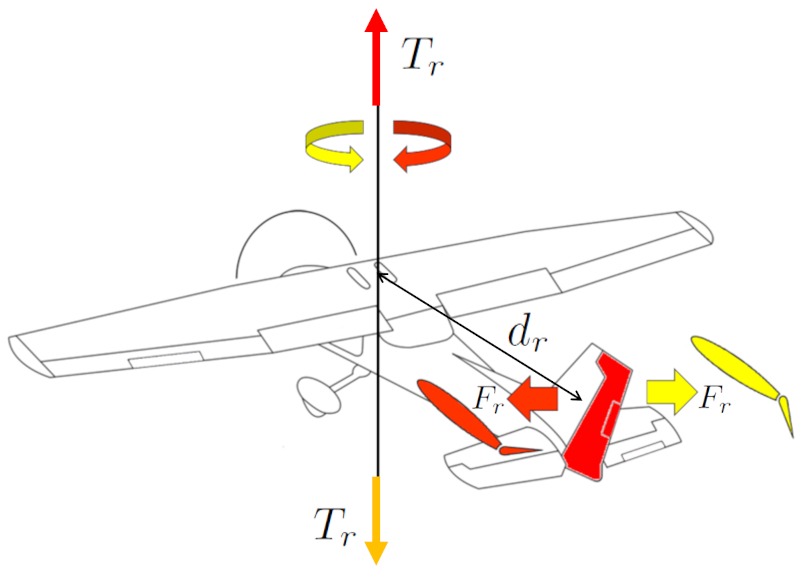
Le pilote contrôle ce mouvement à l'aide des pédales. La direction de la courbe est déterminée par la direction des pédales.
ID:(15162, 0)



