Control
Storyboard 
Para maniobrar la aeronave, se utilizan los elevadores, los alerones y el timón. Todos aprovechan la sustentación generada por el perfil del ala para crear fuerzas en puntos distantes del centro de masa y así inducir torques que provocan la rotación de la aeronave.
ID:(2055, 0)
Control, uso de sustentación
Imagen 
Los alerones son partes de las alas que permiten curvar su extremo hacia arriba (generando fuerza hacia abajo) o hacia abajo (generando fuerza hacia arriba). Todos se encuentran en puntos alejados del centro de masa para lograr una mayor distancia y, por lo tanto, un mayor torque, lo que los hace más efectivos en la rotación.
Debido a la geometría, hay tres ejes alrededor de los cuales el avión gira. El alerón del timón genera una rotación alrededor de un eje vertical. Los alerones de las alas traseras más pequeñas (llamados estabilizadores) permiten una rotación alrededor de un eje perpendicular al eje del avión para subir y bajar el morro del avión. Por último, están los alerones de las alas que permiten que el avión gire alrededor de su eje central.
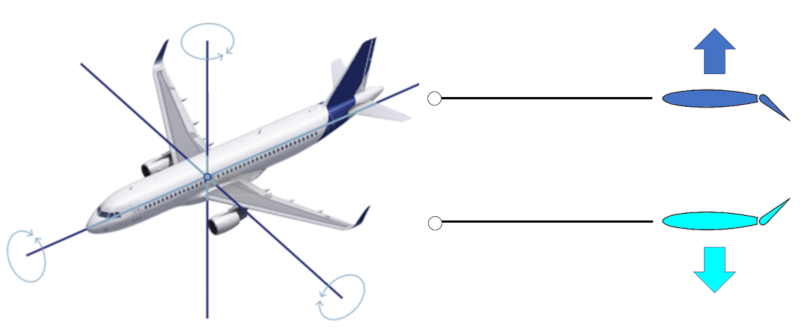
Existen un tipo de alerón que, adicionalmente, es extensible en las alas principales cerca del fuselaje, conocidos como flaps, que permiten aumentar/reducir tanto la superficie del ala como el ángulo de ataque.
Por último, existen superficies que se pueden elevar para perturbar el flujo sobre el ala y se utilizan para frenar, conocidas como spoilers.
ID:(11081, 0)
Control de cabeceo
Nota 
Para realizar giros en la aeronave, se utilizan los elevadores. Estos generan una fuerza en los elevadores ($F_e$) que con una distancia centro de masa y elevadores ($d_e$) induce un torque generado por los elevadores ($T_e$). Los elevadores se encuentra en la cola del avión de modo de maximizar ERROR:10215,0 y lograr un mayor ERROR:10218,0.
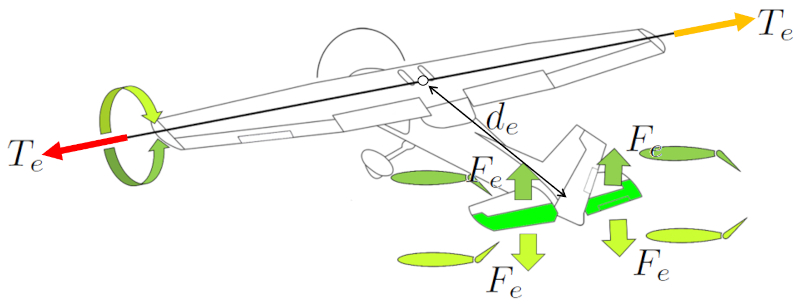
En aviones más antiguos, el control de los alerones traseros se realiza mediante una barra de mando, donde al empujar hacia adelante, la nariz del avión desciende, y al jalar hacia atrás, la nariz se eleva. En los aviones de la familia Airbus, este control se realiza mediante un joystick.
En el caso de las aves, existe una solución similar, aunque en este caso, la cola no está interrumpida por un timón.
ID:(15161, 0)
Aceleración angular de cabeceo
Cita 
A travez de los elevadores se genera una fuerza que induce un torque generado por los elevadores ($T_e$). Este a su vez, dependiendo de el momento de inercia eje del ala ($I_e$) genera una aceleración angular eje del ala ($\alpha_e$) que se muestra en la grafica.

La posibilidad de controlar el angulo de cabeceo es clave en el proceso de despegar en que se debe levantar la nariz lo que aumenta la sustentación. Luego al aterrizar en que es necesario bajar la nariz para reducir la sustentación y con ello decender.
ID:(11079, 0)
Control de rodar
Ejercicio 
Para realizar giros en una aeronave, se utilizan los ailerones. Estos generan una una fuerza en los alerones ($F_a$) que, en conjunto con una distancia centro de masa y alerones ($d_a$), inducen una un torque generado por los alerones ($T_a$). Los ailerones se encuentran en las puntas de las alas de la aeronave para maximizar su la distancia centro de masa y alerones ($d_a$) con respecto al centro de masa y lograr una mayor una distancia centro de masa y elevadores ($d_e$).
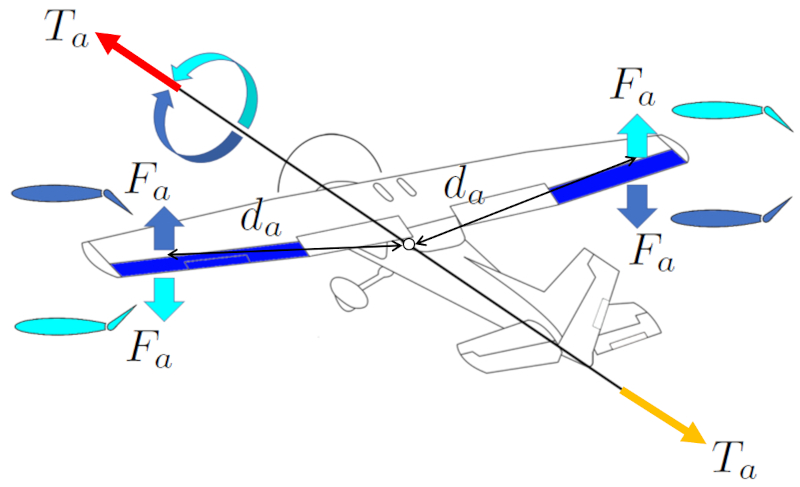
Los ailerones operan de manera asimétrica, lo que significa que si el ailerón del ala derecha genera sustentación hacia arriba, el ailerón del ala izquierda lo hace hacia abajo, y viceversa. De esta forma, estas fuerzas generan un torque que permite girar en sentido horario o antihorario.
El objetivo de la rotación es generar, con la fuerza de sustentación, una fuerza ortogonal al eje central, lo que lleva a una curva en la aeronave. Esto refuerza la acción del timón, ayudando en la maniobra de viraje de la aeronave. De hecho, esta es la forma en que las aves realizan sus maniobras de viraje, ya que no tienen un timón.
Para realizar la maniobra de viraje, el piloto utiliza el control de columna, que tiene un tipo de volante que gira en la misma dirección que la aeronave. En otros casos, como en el joystick de las aeronaves Airbus, no hay un volante, y se inclina el joystick en la dirección deseada para realizar la curva.
Uno de los problemas que surgen al realizar una rotación en torno al eje central de la aeronave es que la fuerza de sustentación se utiliza para desviar la trayectoria, lo que resulta en una disminución de la sustentación. Esto significa que, durante una maniobra de viraje, la aeronave y el ave tienden a perder altura a menos que se incremente la potencia.
ID:(15160, 0)
Aceleración angular de rodar
Ecuación 
A travez de los alerones se genera una fuerza que induce un torque generado por los alerones ($T_a$). Este a su vez, dependiendo de el momento de inercia eje del avión ($I_a$) genera una aceleración angular eje del avión ($\alpha_a$) que se muestra en la grafica.

Los alerones permiten modificar la inclinación del avión ya sea que esta se genero por ejemplo por vientos curzados o se desea para realizar un viraje. Esto ultimo ocurre pues al ladear el avión la fuerza de sustentación crea una componente lateral que lo desvia.
ID:(11078, 0)
Control de guiñada
Script 
Para realizar giros en una aeronave, se utiliza el timón. Este genera una fuerza en el timón ($F_r$), que, combinada con una distancia centro de masa y timón ($d_r$), induce una fuerza en el timón ($F_r$). El timón se encuentra ubicado en la cola del avión para maximizar una la distancia centro de masa y timón ($d_r$) y lograr un mayor una fuerza en el timón ($F_r$).
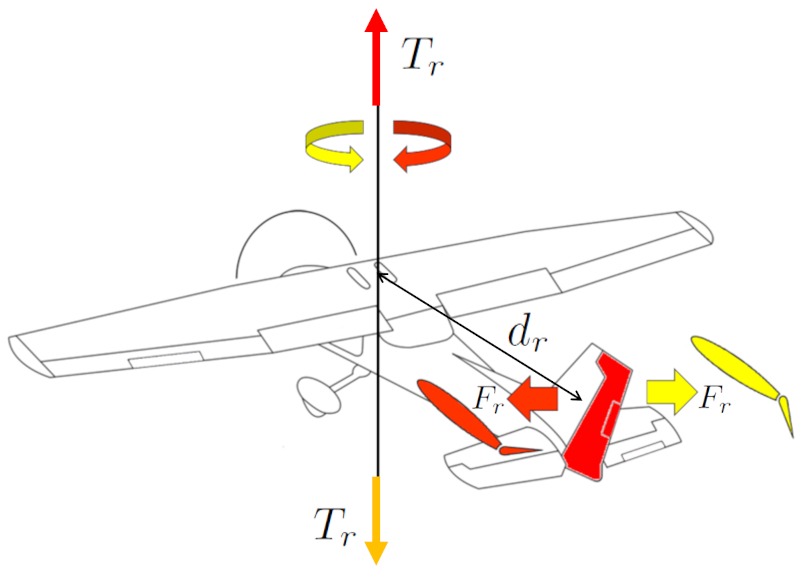
El piloto controla este movimiento utilizando los pedales. La dirección del giro se determina mediante la dirección de los pedales.
ID:(15162, 0)
Aceleración angular de guiñada
Variable 
A travez de el timón se genera una fuerza que induce un torque generado por el timón ($T_r$). Este a su vez, dependiendo de la aceleración angular eje vertical ($\alpha_r$) genera una aceleración angular eje vertical ($\alpha_r$) que se muestra en la grafica.

La posibilidad de controlar el angulo de guiñada sirve para girar la aeronave con mayor precisión de lo que permiten los alerones. Ademas estos ultimos no son efectivos para ello a bajas velocidades o con vientos atravezados.
ID:(11077, 0)
