Usuario:
Velocidad angular instantánea
Storyboard 
La velocidad angular media se define como el ángulo recorrido en un intervalo de tiempo, sin tener en cuenta las posibles fluctuaciones de la velocidad angular.
Para determinar la velocidad angular en un instante específico, es necesario considerar un intervalo de tiempo extremadamente pequeño, de modo que la velocidad angular no tenga variaciones notables en ese período.
Por lo tanto, la velocidad angular instantánea se obtiene calculando la velocidad angular media en el límite de un intervalo de tiempo que tiende a cero. Desde un punto de vista matemático, esto equivale a la derivada del ángulo respecto al tiempo y representa la pendiente de la curva ángulo-tiempo.
ID:(1447, 0)
Velocidad angular como derivada
Concepto
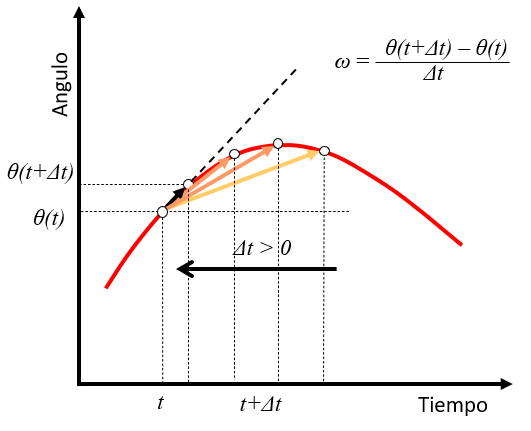
Si se toma un tiempo $t$ con un ángulo $\theta(t)$ y se observa un punto en un tiempo futuro $t+\Delta t$ con un ángulo $\theta(t+\Delta t)$ se puede estimar la velocidad como el ángulo recorrido
$\theta(t+\Delta t)-\theta(t)$
recorrido en el tiempo $\Delta t$
$\omega\sim\displaystyle\frac{\theta(t+\Delta t)-\theta(t)}{\Delta t}$
A medida que se va reduciendo el valor del tiempo $\Delta t$ la velocidad angular va tomando el rol de la tangente a la curva posición en el tiempo:
Autopista con salida
Esto generaliza lo que ya se había visto para lo que es el caso de velocidad angular constante.
ID:(11407, 0)
Segmento área angulo recorrido
Descripción
Si observamos que la velocidad angular $\omega$ es igual al ángulo $\Delta\theta$ multiplicado por el tiempo $\Delta t$, podemos afirmar que el desplazamiento es
$\Delta\theta = \omega\Delta t$
Dado que el producto $\omega\Delta t$ es el área bajo la curva de velocidad angular en función del tiempo, y esto, a su vez, es igual al desplazamiento recorrido:
ID:(11417, 0)
Ángulo como integral de la velocidad angular
Descripción
La integral de una función corresponde al área debajo de la curva que define la función. Por lo tanto, la integral de la velocidad entre los tiempos $t_0$ y $t$ corresponde al ángulo recorrido entre la posición inicial $\theta_0$ y $\theta$.
Esto se puede expresar matemáticamente como:
| $ \theta = \theta_0 +\displaystyle\int_{t_0}^t \omega d\tau$ |
Esta relación se muestra gráficamente a continuación:
Esta fórmula es útil para calcular el ángulo recorrido por un objeto en situaciones en las que se conoce la función de velocidad. La integral de la función de velocidad proporciona una medida del desplazamiento total del objeto entre los dos tiempos $t_0$ y $t$, lo que se puede utilizar para calcular el ángulo recorrido por el objeto dividiendo el desplazamiento por el radio del círculo. Este concepto es especialmente útil en aplicaciones de física e ingeniería en las que se involucra el movimiento de rotación.
ID:(11409, 0)
Velocidad tangencial, regla de la mano derecha
Imagen
La orientación de la velocidad tangencial puede ser obtenida utilizando la regla de la mano derecha. Si los dedos se colocan en dirección del eje de rotación y se rotan hacia el vector de posición (radio), el pulgar apuntará en la dirección de la velocidad tangencial:
ID:(11599, 0)
Velocidad tangencial
Descripción
Si un objeto se somete a un modo de mantener un radio constante, girará como se indica en la figura. Al observar la figura, se notará que la masa realiza un movimiento de traslación con una velocidad tangencial que es igual al radio por la velocidad angular:
Sin embargo, si se corta el elemento que une el objeto al eje, este continuará moviéndose tangencialmente en línea recta.
ID:(310, 0)
Modelo
Top
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
$ \vec{\omega} = \displaystyle\frac{ d\vec{\theta} }{ dt }$
&omega = @DIF( &theta , t )
$ \vec{v} = \vec{\omega} \times \vec{r} $
&v = &omega x &r
$ \omega =\displaystyle\frac{ d\theta }{ dt }$
omega = @DIF( theta , t , 1)
$ \theta = \theta_0 +\displaystyle\int_{t_0}^t \omega d\tau$
theta = theta_0 + @INT( oemga, tau, t_0, t)
$ v_t = r \omega $
v_t = r * omega
ID:(15423, 0)
Velocidad angular instantánea
Ecuación
La la velocidad angular media ($\bar{\omega}$), calculada a partir de una variación del angulo ($\Delta\theta$) y el tiempo transcurrido ($\Delta t$) mediante la ecuación
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
,
es una aproximación de la la velocidad angular instantánea ($\omega$) real que tiende a distorsionarse a medida que la velocidad angular fluctúa durante el intervalo de tiempo. Por lo tanto, se introduce el concepto de la velocidad angular instantánea ($\omega$) determinada en un tiempo muy pequeño. En este caso, hablamos de un intervalo de tiempo infinitesimalmente pequeño.
| $ \omega =\displaystyle\frac{ d\theta }{ dt }$ |
Si consideramos el ángulo recorrido como la variación del angulo ($\Delta\theta$) en el tiempo $t+\Delta t$ y en $t$:
$\Delta\theta = \theta(t+\Delta t)-\theta(t)$
y usamos el tiempo transcurrido ($\Delta t$), entonces, en el límite de tiempos infinitesimalmente cortos:
$\omega=\displaystyle\frac{\Delta\theta}{\Delta t}=\displaystyle\frac{\theta(t+\Delta t)-\theta(t)}{\Delta t}\rightarrow lim_{\Delta t\rightarrow 0}\displaystyle\frac{\theta(t+\Delta t)-\theta(t)}{\Delta t}=\displaystyle\frac{d\theta}{dt}$
Esta última expresión corresponde a la derivada de la función de ángulo $\theta(t)$, que a su vez es la pendiente de la representación gráfica de dicha función en el tiempo.
que corresponde a la derivada del ángulo.
ID:(3232, 0)
Integración de la velocidad angular
Ecuación
Como el tiempo ($t$) es la derivada de el ángulo ($\theta$) respecto a la velocidad angular instantánea ($\omega$), es decir,
| $ \omega =\displaystyle\frac{ d\theta }{ dt }$ |
,
la integración de el tiempo ($t$) entre el tiempo inicial ($t_0$) y el tiempo ($t$) corresponde al ángulo recorrido entre el ángulo inicial ($\theta_0$) y el ángulo ($\theta$), como se demuestra en
| $ \theta = \theta_0 +\displaystyle\int_{t_0}^t \omega d\tau$ |
.
ID:(11408, 0)
Velocidad tangencial
Ecuación
Si se divide el camino expresado como arco de un circulo se tendrá que con es
| $ \Delta s=r \Delta\theta $ |
por el tiempo transcurrido
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
y como la velocidad angular con es
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
se tiene con la relación
| $ v_t = r \omega $ |
ID:(10968, 0)
Velocidad tangencial, forma vectorial
Ecuación
La velocidad angular instantánea ($\omega$) se define como un vector cuya dirección coincide con el eje de rotación. Dado que el eje de rotación el radio ($r$) y la velocidad angular instantánea ($\omega$) son perpendiculares a la velocidad ($v$), se puede expresar como el producto vectorial entre la velocidad angular instantánea ($\omega$) y el eje de rotación el radio ($r$):
| $ v = r \omega $ |
la velocidad ($v$) se puede escribir en forma vectorial como la velocidad (vector) ($\vec{v}$), resultado del producto cruz entre la velocidad angular ($\vec{\omega}$) y el radio (vector) ($\vec{r}$):
| $ \vec{v} = \vec{\omega} \times \vec{r} $ |
Dado que la velocidad ($v$) está con la velocidad angular instantánea ($\omega$) y el radio ($r$) es igual a:
| $ v = r \omega $ |
podemos calcular la velocidad (vector) ($\vec{v}$) utilizando el producto cruzado con el versor del eje, denotado como $\hat{n}$, y el versor radial, denotado como $\hat{r}$:
$\hat{t} = \hat{n} \times \hat{r}$
Por lo tanto, si definimos
$\vec{v}=v\hat{t}$
,
$\vec{r}=r\hat{r}$
y
$\vec{\omega}=\omega\hat{n}$
,
entonces podemos expresar la velocidad como
$\vec{v}=v\hat{t}=v\hat{n}\times\hat{r}=r\omega\hat{n}\times\hat{r}=\vec{\omega}\times\vec{r}$
es decir
| $ \vec{v} = \vec{\omega} \times \vec{r} $ |
ID:(11597, 0)
Velocidad angular instantánea en más dimensiones
Ecuación
En general, la velocidad angular instantánea ($\omega$) debe entenderse como una entidad tridimensional, es decir, un vector la velocidad angular ($\vec{\omega}$). Cada componente se puede definir como la derivada de el ángulo ($\theta$) respecto a el tiempo ($t$):
| $ \omega =\displaystyle\frac{ d\theta }{ dt }$ |
Por lo tanto, se puede expresar con la derivada en el tiempo ($t$) de el ángulo (vector) ($\vec{\theta}$) como la velocidad angular ($\vec{\omega}$):
| $ \vec{\omega} = \displaystyle\frac{ d\vec{\theta} }{ dt }$ |
ID:(9878, 0)