User:
Instant angular speed
Storyboard 
The average angular velocity is defined by considering the angle traversed over a time interval, without taking into account any possible fluctuations in angular velocity.
To determine the angular velocity at a specific instant, it is necessary to consider an extremely small time interval, so that the angular velocity does not exhibit significant changes during that period.
Therefore, the instantaneous angular velocity is obtained by calculating the average angular velocity as the limit of a time interval approaching zero. From a mathematical standpoint, this is equivalent to taking the derivative of the angle with respect to time and represents the slope of the angle-time curve.
ID:(1447, 0)
Angular speed as a derivative
Concept
If we take a time $t$ with an angle $\theta(t)$ and observe a point at a future time $t+\Delta t$ with an angle $\theta(t+\Delta t)$, we can estimate the velocity as the angle traveled
$\theta(t+\Delta t)-\theta(t)$
in the time $\Delta t$.
$\omega\sim\displaystyle\frac{\theta(t+\Delta t)-\theta(t)}{\Delta t}$
As the value of time $\Delta t$ is reduced, the angular velocity takes on the role of the tangent to the position curve at that time:
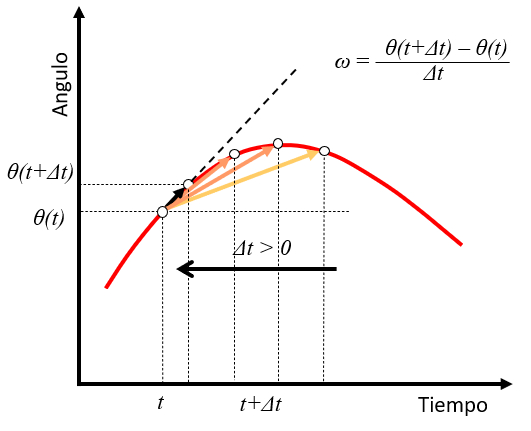
This generalizes what has already been seen for the case of constant angular velocity.
ID:(11407, 0)
Segment area angle traveled
Description
If we observe that the angular velocity $\omega$ is equal to the angle $\Delta\theta$ multiplied by the time $\Delta t$, we can state that the displacement is
$\Delta\theta = \omega\Delta t$
Since the product $\omega\Delta t$ represents the area under the curve of angular velocity versus time, and this area is also equal to the displacement traveled:
ID:(11417, 0)
Angle as an integral of angular velocity
Description
The integral of a function corresponds to the area under the curve that defines the function. Therefore, the integral of velocity between times $t_0$ and $t$ corresponds to the angle traveled between the initial position $\theta_0$ and $\theta$.
This can be expressed mathematically as:
| $ \theta = \theta_0 +\displaystyle\int_{t_0}^t \omega d\tau$ |
This relationship is shown graphically below:
This formula is useful for calculating the angle traveled by an object in situations where the velocity function is known. The integral of the velocity function provides a measure of the total displacement of the object between the two times $t_0$ and $t$, which can be used to calculate the angle traveled by the object by dividing the displacement by the radius of the circle. This concept is particularly useful in physics and engineering applications where rotational motion is involved.
ID:(11409, 0)
Tangential speed, right hand rule
Image
The orientation of the tangential velocity can be obtained using the right-hand rule. If the fingers point towards the axis of rotation and then are curled towards the position vector (radius), the thumb will point in the direction of the tangential velocity:
ID:(11599, 0)
Tangential speed
Description
If an object is subjected to a mode of maintaining a constant radius, it will rotate as indicated in the figure. Upon observing the figure, one would notice that the mass undergoes a translational motion with a tangential velocity that is equal to the radius times the angular velocity:
However, if the element connecting the object to the axis is cut, the object will continue to move tangentially in a straight line.
ID:(310, 0)
Model
Top
Calculations
Variables
Parameters
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used Equation
$ \vec{\omega} = \displaystyle\frac{ d\vec{\theta} }{ dt }$
&omega = @DIF( &theta , t )
$ \vec{v} = \vec{\omega} \times \vec{r} $
&v = &omega x &r
$ \omega =\displaystyle\frac{ d\theta }{ dt }$
omega = @DIF( theta , t , 1)
$ \theta = \theta_0 +\displaystyle\int_{t_0}^t \omega d\tau$
theta = theta_0 + @INT( oemga, tau, t_0, t)
$ v_t = r \omega $
v_t = r * omega
ID:(15423, 0)
Instantaneous Angular Velocity
Equation
The the mean angular velocity ($\bar{\omega}$), calculated from ($$) and the time elapsed ($\Delta t$) using the equation
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
,
is an approximation of the real the instantaneous Angular Speed ($\omega$) that tends to distort as the angular velocity fluctuates over the time interval. Therefore, the concept of the instantaneous Angular Speed ($\omega$) determined at a very small time is introduced. In this case, we are talking about an infinitesimally small time interval.
| $ \omega =\displaystyle\frac{ d\theta }{ dt }$ |
If we consider the angle covered as the angle variation ($\Delta\theta$) at time $t+\Delta t$ and at $t$:
$\Delta\theta = \theta(t+\Delta t)-\theta(t)$
and use the time elapsed ($\Delta t$), then, in the limit of infinitesimally short times:
$\omega=\displaystyle\frac{\Delta\theta}{\Delta t}=\displaystyle\frac{\theta(t+\Delta t)-\theta(t)}{\Delta t}\rightarrow lim_{\Delta t\rightarrow 0}\displaystyle\frac{\theta(t+\Delta t)-\theta(t)}{\Delta t}=\displaystyle\frac{d\theta}{dt}$
This last expression corresponds to the derivative of the angle function $\theta(t)$, which in turn is the slope of the graphical representation of that function over time.
which corresponds to the derivative of the angle.
ID:(3232, 0)
Angular Speed integration
Equation
As the time ($t$) represents the derivative of the angle ($\theta$) with respect to the instantaneous Angular Speed ($\omega$), i.e.,
| $ \omega =\displaystyle\frac{ d\theta }{ dt }$ |
,
integrating the time ($t$) between the start Time ($t_0$) and the time ($t$) corresponds to the angle traveled between the initial Angle ($\theta_0$) and the angle ($\theta$), as demonstrated in
| $ \theta = \theta_0 +\displaystyle\int_{t_0}^t \omega d\tau$ |
ID:(11408, 0)
Tangential speed
Equation
Si se divide el camino expresado como arco de un circulo se tendrá que con es
| $ \Delta s=r \Delta\theta $ |
por el tiempo transcurrido
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
y como la velocidad angular con es
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
se tiene con la relación
| $ v_t = r \omega $ |
ID:(10968, 0)
Tangential speed, vector shape
Equation
The instantaneous Angular Speed ($\omega$) is defined as a vector whose direction coincides with the axis of rotation. Since the rotation axis the radius ($r$) and the instantaneous Angular Speed ($\omega$) are perpendicular to the speed ($v$), it can be expressed as the cross product between the instantaneous Angular Speed ($\omega$) and the rotation axis the radius ($r$):
| $ v = r \omega $ |
the speed ($v$) can be written in vector form as the speed (Vector) ($\vec{v}$), resulting from the cross product of the angular Speed ($\vec{\omega}$) with the radius (vector) ($\vec{r}$):
| $ \vec{v} = \vec{\omega} \times \vec{r} $ |
Since the speed ($v$) is with the instantaneous Angular Speed ($\omega$) and the radio ($r$) equals:
| $ v = r \omega $ |
we can calculate the speed (Vector) ($\vec{v}$) using the cross product with the axis unit vector, denoted as $\hat{n}$, and the radial unit vector, denoted as $\hat{r}$:
$\hat{t} = \hat{n} \times \hat{r}$
Therefore, if we define
$\vec{v}=v\hat{t}$
,
$\vec{r}=r\hat{r}$
and
$\vec{\omega}=\omega\hat{n}$
,
then we can express the velocity as
$\vec{v}=v\hat{t}=v\hat{n}\times\hat{r}=r\omega\hat{n}\times\hat{r}=\vec{\omega}\times\vec{r}$
meaning
| $ \vec{v} = \vec{\omega} \times \vec{r} $ |
ID:(11597, 0)
Instantaneous angular velocity in more dimensions
Equation
In general, the instantaneous Angular Speed ($\omega$) should be understood as a three-dimensional entity, that is, a vector the angular Speed ($\vec{\omega}$). Each component can be defined as the derivative of the angle ($\theta$) with respect to the time ($t$):
| $ \omega =\displaystyle\frac{ d\theta }{ dt }$ |
Thus, it can be expressed with the derivative in the time ($t$) of the angle (vector) ($\vec{\theta}$) as the angular Speed ($\vec{\omega}$):
| $ \vec{\omega} = \displaystyle\frac{ d\vec{\theta} }{ dt }$ |
ID:(9878, 0)