Aceleración angular instantanea
Storyboard 
Para describir cómo evoluciona la velocidad angular en el tiempo, es necesario estudiar su variación a lo largo del tiempo.
La relación de la variación de la velocidad angular equivale al cambio en la velocidad angular en el tiempo transcurrido, que al dividirse por este, corresponde a la aceleración angular.
Para un intervalo de tiempo infinitesimal, la aceleración angular corresponde a la aceleración angular instantánea.
ID:(1452, 0)
Aceleración angular como derivada
Imagen 
Si se toma un intervalo de tiempo $t$ con una velocidad angular $\omega(t)$ y se observa un punto en un momento futuro $t+\Delta t$ con una velocidad angular $\omega(t+\Delta t)$, la aceleración angular puede estimarse como la variación
$\omega(t+\Delta t)-\omega(t)$
en el transcurso del tiempo $\Delta t$:
$\alpha\sim\displaystyle\frac{\omega(t+\Delta t)-\omega(t)}{\Delta t}$
A medida que el valor de $\Delta t$ disminuye, la aceleración toma el papel de la tangente a la curva de velocidad en ese momento:
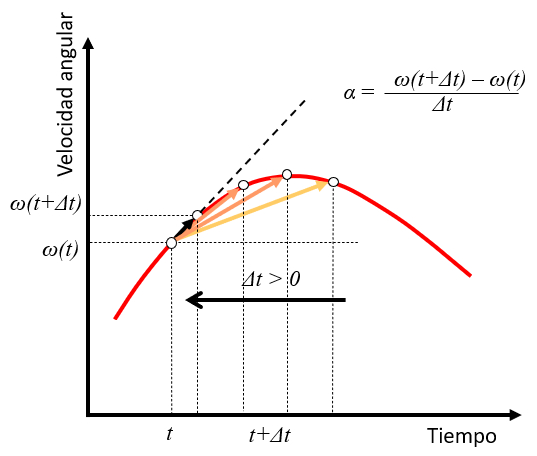
Esto generaliza lo que ya se ha visto en el caso de la aceleración angular constante.
ID:(11413, 0)
Velocidad angular como integral de la aceleración
Nota 
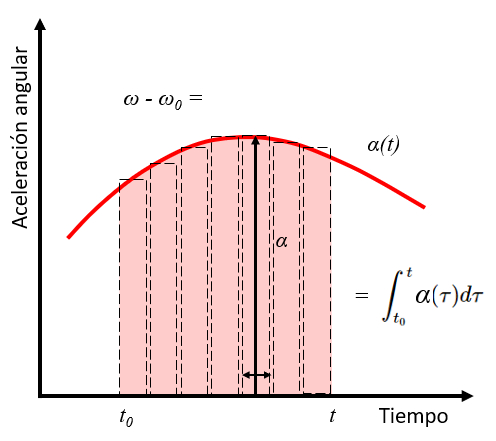
La integral de una función corresponde al área bajo la curva que define dicha función. Por lo tanto, la integral de la aceleración angular entre los tiempos $t_0$ y $t$ corresponde a la variación de la velocidad angular entre la velocidad angular inicial $\omega_0$ y $\omega$.
Por lo tanto, utilizando aceleración angular instantánea $rad/s^2$, tiempo $s$, tiempo inicial $s$, velocidad angular $rad/s$ y velocidad angular inicial $rad/s$, obtenemos:
| $ \omega = \omega_0 +\displaystyle\int_{t_0}^t \alpha\,d\tau $ |
Lo cual se muestra en el siguiente gráfico:
ID:(11415, 0)
Aceleración tangencial, regla de la mano derecha
Cita 
La dirección de la aceleración tangencial puede determinarse utilizando la regla de la mano derecha, donde los dedos se orientan hacia el eje y luego se giran en dirección al radio:

ID:(11600, 0)
Aceleración angular instantanea
Descripción 
Para describir cómo evoluciona la velocidad angular en el tiempo, es necesario estudiar su variación a lo largo del tiempo. La relación de la variación de la velocidad angular equivale al cambio en la velocidad angular en el tiempo transcurrido, que al dividirse por este, corresponde a la aceleración angular. Para un intervalo de tiempo infinitesimal, la aceleración angular corresponde a la aceleración angular instantánea.
Variables
Cálculos
Cálculos
Ecuaciones
Dado que la aceleraci n tangencial es
| $ a = r \alpha $ |
Si el versor del eje es $\hat{n}$ y el radial es $\hat{r}$, el versor tangencial puede calcularse mediante el producto cruz:
$\hat{t} = \hat{n} \times \hat{r}$
En consecuencia, considerando que
$\vec{a} = a \hat{t}$
,
$\vec{r} = r \hat{r}$
y
$\vec{\alpha} = \alpha \hat{n}$
,
podemos deducir que
$\vec{a} = a \hat{t} = a \hat{n} \times \hat{r} = r \alpha \hat{n} \times \hat{r} = \vec{\alpha} \times \vec{r}$
,
lo que se traduce en
| $ \vec{a} = \vec{\alpha} \times \vec{r} $ |
(ID 11598)
Ejemplos
(ID 15415)
Si se toma un intervalo de tiempo $t$ con una velocidad angular $\omega(t)$ y se observa un punto en un momento futuro $t+\Delta t$ con una velocidad angular $\omega(t+\Delta t)$, la aceleraci n angular puede estimarse como la variaci n
$\omega(t+\Delta t)-\omega(t)$
en el transcurso del tiempo $\Delta t$:
$\alpha\sim\displaystyle\frac{\omega(t+\Delta t)-\omega(t)}{\Delta t}$
A medida que el valor de $\Delta t$ disminuye, la aceleraci n toma el papel de la tangente a la curva de velocidad en ese momento:

Esto generaliza lo que ya se ha visto en el caso de la aceleraci n angular constante.
(ID 11413)
La integral de una funci n corresponde al rea bajo la curva que define dicha funci n. Por lo tanto, la integral de la aceleraci n angular entre los tiempos $t_0$ y $t$ corresponde a la variaci n de la velocidad angular entre la velocidad angular inicial $\omega_0$ y $\omega$.
Por lo tanto, utilizando aceleración angular instantánea $rad/s^2$, tiempo $s$, tiempo inicial $s$, velocidad angular $rad/s$ y velocidad angular inicial $rad/s$, obtenemos:
| $ \omega = \omega_0 +\displaystyle\int_{t_0}^t \alpha\,d\tau $ |
Lo cual se muestra en el siguiente gr fico:

(ID 11415)
La direcci n de la aceleraci n tangencial puede determinarse utilizando la regla de la mano derecha, donde los dedos se orientan hacia el eje y luego se giran en direcci n al radio:

(ID 11600)
(ID 15426)
Al igual que en la aceleraci n de traslaci n, existe el concepto de aceleraci n angular instant nea, que es la aceleraci n angular con
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
que existe en un tiempo espec fico. Esto se calcula en la aproximaci n de intervalos de tiempo muy peque os $(\Delta t\rightarrow 0)$, es decir
$\alpha=\lim_{\Delta t\rightarrow 0}\displaystyle\frac{\Delta\omega}{\Delta t}=\displaystyle\frac{d\omega}{dt}$
donde
| $ \alpha =\displaystyle\frac{ d\omega }{ dt }$ |
(ID 3235)
Si integramos en el tiempo la definici n de la velocidad angular con aceleración angular instantánea $rad/s^2$, tiempo $s$ y velocidad angular instantánea $rad/s$, obtenemos:
| $ \alpha =\displaystyle\frac{ d\omega }{ dt }$ |
lo que significa que para un intervalo de tiempo $dt$, el ngulo recorrido es:
$d\omega = \alpha dt$
Si consideramos $N$ intervalos $dt_i$ con velocidades angulares $\alpha_i$, el ngulo total recorrido ser :
$\omega - \omega_0 = \displaystyle\sum_i \alpha_i dt_i$
Si consideramos la curva de velocidad angular-tiempo, los elementos $\alpha_i dt_i$ corresponden a rect ngulos con altura $\alpha_i$ y ancho $dt_i$. La suma, por lo tanto, corresponde al rea bajo la curva de velocidad angular-tiempo. Por lo tanto, la suma se puede expresar como una integral utilizando aceleración angular instantánea $rad/s^2$, tiempo $s$ y velocidad angular instantánea $rad/s$:
| $ \omega = \omega_0 +\displaystyle\int_{t_0}^t \alpha\,d\tau $ |
(ID 11416)
En general hay que entender la aceleraci n como un ente en tres dimensiones, es decir vectorial. Esto es su velocidad requiere ser descrita por un vector velocidad angular $\vec{\omega}$ para el cual se puede definir componente una aceleraci n con aceleración angular instantánea $rad/s^2$, tiempo $s$ y velocidad angular instantánea $rad/s$
| $ \alpha =\displaystyle\frac{ d\omega }{ dt }$ |
con lo que se puede generalizar la aceleraci n con:
| $ \vec{alpha} =\displaystyle\frac{d \vec{\omega} }{d t }$ |
(ID 6742)
La integraci n de la definici n diferencial, es decir, de las variaciones temporales infinitesimales, con respecto a la ecuaci n da como resultado:
| $ a =\displaystyle\frac{ d v }{ d t }$ |
Podemos realizar la integraci n entre el tiempo $t_0$ y $t$ de la aceleraci n $a(\tau)$ para obtener la velocidad $v(t)$ si la velocidad inicial es $v_0$, utilizando la ecuaci n:
| $ v = v_0 +\displaystyle\int_{t_0}^t a(\tau) d\tau $ |
(ID 11414)
La aceleraci n angular se expresa como un vector en la direcci n del eje de rotaci n. Dado que el radio de rotaci n y la aceleraci n angular son perpendiculares a la aceleraci n tangencial, se obtiene la siguiente relaci n:
| $ a = r \alpha $ |
Esta relaci n puede escribirse como el producto cruz entre la aceleraci n angular y el radio, representado de la siguiente manera:
| $ \vec{a} = \vec{\alpha} \times \vec{r} $ |
(ID 11598)
ID:(1452, 0)
