User:
Surface model
Storyboard 
The transfer of particles or molecules, such as CO2, between the atmosphere and the ocean involves a more complex mechanism. This process is associated with the formation of a liquid film saturated with particles or molecules, which regulates the movement of new particles to or from the interior of the ocean.
ID:(1633, 0)
Mechanisms
Iframe
Mechanisms
ID:(15640, 0)
Surface layer
Description
To study the transfer of CO2 at the ocean surface, it is necessary to carefully observe the concentration changes in both the air and the water.
In the air, CO2 enters the water, creating a zone of low concentration where it decreases from $C_a$ to $C_{a,0}$. This layer has a thickness ranging from 0.1 to 1 mm.
The CO2 that enters the water initially accumulates at the surface, creating a concentration $C_{w,0}$, which then diffuses into the interior, reaching a lower concentration of $C_w$.
The concentration reduction allows us to define two zones: a very thin one, ranging from 0.02 to 0.2 mm, where the concentration decreases rapidly, and a second zone, spanning from 0.6 to 2 mm, where the concentration decreases more gradually until it reaches the concentration within the water.
Ocean-Atmosphere Interactions of Gases and Particles, Peter S. Liss, Martin T. Johnson (eds.), Springer-Verlag Berlin Heidelberg
ID:(12244, 0)
CO2 exchange, speed from water
Concept
The gas transfer rate in water ($k_w$) can be modeled using measured data. Firstly, it depends on the rate at which the system removes carbon from the air-water interface, making the transport speed proportional to the relative velocity between the two mediums.
Secondly, there is an effect of ion mobility, which can be described by the schmidt number ($Sc$), representing the relationship between momentum diffusion and particles. However, this dependence is not linear and is influenced by a factor exponente de Schmidt ($n$) that varies between -1/2 and -2/3 depending on the surface roughness.
Finally, the gas transfer rate in water ($k_w$) also depends on the factor beta del transporte aire a agua de CO2 ($\beta$), which in turn is determined by the level of surface roughness.
In summary, the gas the gas transfer rate in water ($k_w$) is described as a function of the velocidad del agua ($u_w$), the velocidad del aire ($u_a$), the schmidt number ($Sc$), the factor beta del transporte aire a agua de CO2 ($\beta$), and exponente de Schmidt ($n$) as follows:
| $ k_w = ( u_a - u_w ) \beta Sc ^ n $ |
ID:(15652, 0)
Solubility as a function of Schmidt number
Concept
The mobility of molecules, represented by the gas solubility ($\alpha$), is modeled as a function of particle concentration, characterized by the schmidt number ($Sc$), which in turn is calculated from parameters the viscosidad en masa acuosa ($\eta$), the densidad en capa de masa acuosa ($\rho$), and the constante de difusión en masa acuosa ($D$) using the following expression:
| $ Sc =\displaystyle\frac{ \eta }{ \rho D }$ |
This relationship is visualized in the following diagram:
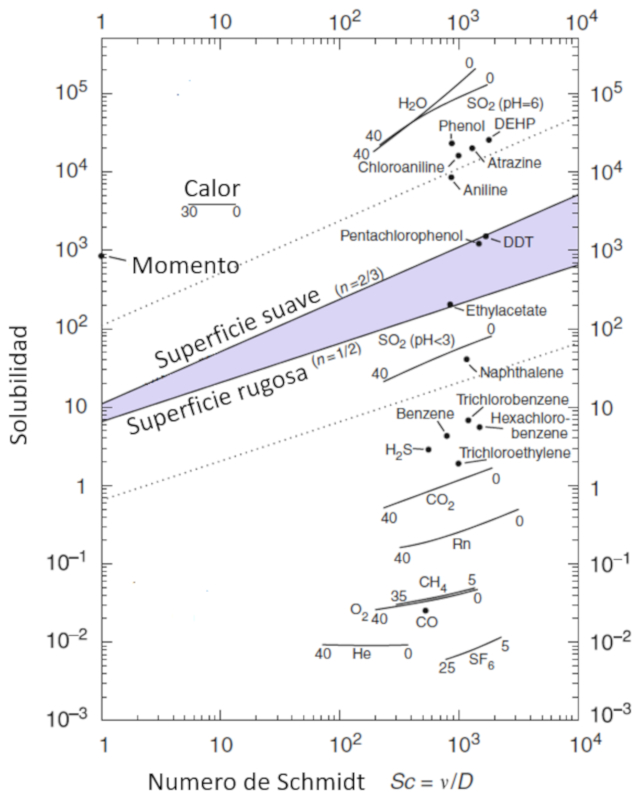
Ocean-Atmosphere Interactions of Gases and Particles, Peter S. Liss, Martin T. Johnson (eds.), Springer-Verlag Berlin Heidelberg
ID:(12245, 0)
Transfer speed
Concept
The gas transfer rate in air ($k_a$) can be estimated from Fick's law by comparing the constante de difusión en masa acuosa ($D$) with the grosor de la capa superficial ($\delta_c$) as follows:
| $ k_a = \displaystyle\frac{ D }{ \delta_c }$ |
ID:(15653, 0)
Transfer speed and resistances
Concept
For the interaction between the atmosphere and the ocean, the air to water transfer resistance of a gas ($R_{ta}$) initially encompasses the transfer resistance in water ($R_w$), followed by the evaporation process $1/\alpha$ with the gas solubility ($\alpha$), and once the gas has passed into the air, the transfer resistance in air ($R_a$) acts upon it:
| $ R_{ta} = R_a + \displaystyle\frac{1}{ \alpha } R_w $ |
Meanwhile, in the interaction between the atmosphere and the ocean, the water to air transfer resistance of a gas ($R_{tw}$) initially includes the transfer resistance in air ($R_a$), followed by the gas solubility ($\alpha$), and once the gas has penetrated the water, the transfer resistance in water ($R_w$) comes into play:
| $ R_{tw} = R_w + \alpha R_a $ |
With these equations, we can formulate the relationships for the transfer velocities.
Therefore, using the total transfer rate of gas in air ($k_{ta}$), the gas transfer rate in water ($k_w$), the gas transfer rate in air ($k_a$), and the gas solubility ($\alpha$), we establish the following relationship:
| $ \displaystyle\frac{1}{ k_{ta} } = \displaystyle\frac{1}{ k_a } + \displaystyle\frac{1}{ \alpha k_w } $ |
On the other hand, with the total transfer rate of gas in water ($k_{tw}$), the gas transfer rate in water ($k_w$), the gas transfer rate in air ($k_a$), and the gas solubility ($\alpha$), we establish that:
| $ \displaystyle\frac{1}{ k_{tw} } = \displaystyle\frac{1}{ k_w } + \displaystyle\frac{ \alpha }{ k_a } $ |
ID:(15654, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ \displaystyle\frac{1}{ k_{ta} } = \displaystyle\frac{1}{ k_a } + \displaystyle\frac{1}{ \alpha k_w } $
1/ k_ta = 1/ k_a + 1/( k_w * alpha )
$ \displaystyle\frac{1}{ k_{tw} } = \displaystyle\frac{1}{ k_w } + \displaystyle\frac{ \alpha }{ k_a } $
1/ k_tw = 1/ k_w + alpha / k_a
$ C_w = \alpha C_a $
C_w = alpha * C_a
$ k_a = \displaystyle\frac{ D }{ \delta_c }$
k_a = D / delta_c
$ k_w = ( u_a - u_w ) \beta Sc ^ n $
k_w = ( u_a - u_w )* beta * Sc ^ n
$ R_a = \displaystyle\frac{1}{ k_a } $
R_a = 1/ k_a
$ R_{ta} = \displaystyle\frac{1}{ k_{ta} } $
R_ta = 1/ k_ta
$ R_{ta} = R_a + \displaystyle\frac{1}{ \alpha } R_w $
R_ta = R_a + R_w / alpha
$ R_{tw} = \displaystyle\frac{1}{ k_{tw} } $
R_tw = 1/ k_tw
$ R_{tw} = R_w + \alpha R_a $
R_tw = R_w + alpha * R_a
$ R_w = \displaystyle\frac{1}{ k_w } $
R_w = 1/ k_w
ID:(15645, 0)
Surface Concentration Relationships
Equation
The concentration gradient between the gas concentration in the atmosphere ($C_a$) and the gas concentration in water ($C_{w,0}$) depends on the gas solubility ($\alpha$). Therefore, the following relationship is established:
| $ C_w = \alpha C_a $ |
ID:(12235, 0)
Transfer speed
Equation
The gas transfer rate in air ($k_a$) can be estimated from Fick's law by comparing the constante de difusión en masa acuosa ($D$) with the grosor de la capa superficial ($\delta_c$) as follows:
| $ k_a = \displaystyle\frac{ D }{ \delta_c }$ |
ID:(12227, 0)
CO2 exchange, speed from water
Equation
The gas parameter the gas transfer rate in water ($k_w$) is described in terms of the velocidad del agua ($u_w$), the velocidad del aire ($u_a$), the schmidt number ($Sc$), the factor beta del transporte aire a agua de CO2 ($\beta$), and exponente de Schmidt ($n$) as follows:
| $ k_w = ( u_a - u_w ) \beta Sc ^ n $ |
ID:(12215, 0)
Transfer rate and resistance in the atmosphere
Equation
The transfer resistance in air ($R_a$) is defined as the inverse of the gas transfer rate in air ($k_a$). This relationship can be expressed as follows:
| $ R_a = \displaystyle\frac{1}{ k_a } $ |
ID:(12236, 0)
Transfer rate and resistance in the ocean
Equation
The transfer resistance in water ($R_w$) is defined as the inverse of the gas transfer rate in water ($k_w$). This relationship can be expressed as follows:
| $ R_w = \displaystyle\frac{1}{ k_w } $ |
ID:(12237, 0)
Total atmosphere-ocean transfer rate
Equation
The water to air transfer resistance of a gas ($R_{tw}$) is defined as the inverse of the total transfer rate of gas in water ($k_{tw}$). This relationship can be expressed as follows:
| $ R_{tw} = \displaystyle\frac{1}{ k_{tw} } $ |
ID:(12238, 0)
Total ocean-atmosphere transfer rate
Equation
The air to water transfer resistance of a gas ($R_{ta}$) is defined as the inverse of the total transfer rate of gas in air ($k_{ta}$). This relationship can be expressed as follows:
| $ R_{ta} = \displaystyle\frac{1}{ k_{ta} } $ |
ID:(12239, 0)
Total resistance to ocean-atmosphere transfer
Equation
For the interaction between the atmosphere and the ocean, the air to water transfer resistance of a gas ($R_{ta}$) initially includes the transfer resistance in water ($R_w$), followed by the evaporation process $1/\alpha$ with the gas solubility ($\alpha$). Once the gas has transferred to the air, the transfer resistance in air ($R_a$) acts on it:
| $ R_{ta} = R_a + \displaystyle\frac{1}{ \alpha } R_w $ |
ID:(12240, 0)
Total resistance to atmosphere-ocean transfer
Equation
For the interaction between the atmosphere and the ocean, the water to air transfer resistance of a gas ($R_{tw}$) initially includes the transfer resistance in air ($R_a$), followed by the gas solubility ($\alpha$), and once the gas has penetrated the water, the transfer resistance in water ($R_w$) acts:
| $ R_{tw} = R_w + \alpha R_a $ |
ID:(12241, 0)
Atmosphere-Ocean Transfer Rate
Equation
The relationship between the transfer resistance between the atmosphere and the ocean can be expressed in terms of the transfer speeds in both mediums, equating to the inverse of the total transfer speed.
Therefore, with the total transfer rate of gas in water ($k_{tw}$), the gas transfer rate in water ($k_w$), the gas transfer rate in air ($k_a$), and the gas solubility ($\alpha$), it is established that:
| $ \displaystyle\frac{1}{ k_{tw} } = \displaystyle\frac{1}{ k_w } + \displaystyle\frac{ \alpha }{ k_a } $ |
The relationship between the water to air transfer resistance of a gas ($R_{tw}$), established through the sums of the transfer resistance in water ($R_w$), the transfer resistance in air ($R_a$), and the gas solubility ($\alpha$), is expressed in the equation:
| $ R_{tw} = R_w + \alpha R_a $ |
Including the relationship of the transfer resistance in air ($R_a$) with the gas transfer rate in air ($k_a$) in:
| $ R_a = \displaystyle\frac{1}{ k_a } $ |
The interaction of the transfer resistance in water ($R_w$) with the gas transfer rate in water ($k_w$) is described in:
| $ R_w = \displaystyle\frac{1}{ k_w } $ |
And the connection between the water to air transfer resistance of a gas ($R_{tw}$) and the total transfer rate of gas in water ($k_{tw}$) is detailed in:
| $ R_{tw} = \displaystyle\frac{1}{ k_{tw} } $ |
This provides the basis for establishing the relationship for the total transfer rate of gas in water ($k_{tw}$):
| $ \displaystyle\frac{1}{ k_{tw} } = \displaystyle\frac{1}{ k_w } + \displaystyle\frac{ \alpha }{ k_a } $ |
ID:(12243, 0)
Ocean-atmosphere transfer rate
Equation
The relationship of the transfer resistance between the ocean and the atmosphere can be expressed in terms of the transfer speeds in both mediums, corresponding to the inverse of the total transfer speed.
Thus, using the total transfer rate of gas in air ($k_{ta}$), the gas transfer rate in water ($k_w$), the gas transfer rate in air ($k_a$), and the gas solubility ($\alpha$), the following relationship is established:
| $ \displaystyle\frac{1}{ k_{ta} } = \displaystyle\frac{1}{ k_a } + \displaystyle\frac{1}{ \alpha k_w } $ |
The relationship involving the air to water transfer resistance of a gas ($R_{ta}$), determined by the combination of the transfer resistance in water ($R_w$), the transfer resistance in air ($R_a$), and the gas solubility ($\alpha$), is formulated in the equation:
| $ R_{ta} = R_a + \displaystyle\frac{1}{ \alpha } R_w $ |
This includes the relationship of the transfer resistance in air ($R_a$) with the gas transfer rate in air ($k_a$) expressed in:
| $ R_a = \displaystyle\frac{1}{ k_a } $ |
Additionally, the interaction of the transfer resistance in water ($R_w$) with the gas transfer rate in water ($k_w$) is explained in:
| $ R_w = \displaystyle\frac{1}{ k_w } $ |
And the connection between the air to water transfer resistance of a gas ($R_{ta}$) and the total transfer rate of gas in air ($k_{ta}$) is specified in:
| $ R_{ta} = \displaystyle\frac{1}{ k_{ta} } $ |
These elements together provide the basis for defining the relationship for the total transfer rate of gas in air ($k_{ta}$):
| $ \displaystyle\frac{1}{ k_{ta} } = \displaystyle\frac{1}{ k_a } + \displaystyle\frac{1}{ \alpha k_w } $ |
ID:(12242, 0)