Utilisateur:
Modèle surfacique
Storyboard 
Le transfert de particules ou de molécules, telles que le CO2, entre l'atmosphère et l'océan implique un mécanisme plus complexe. Ce processus est associé à la formation d'un film liquide saturé de particules ou de molécules, qui régule le passage de nouvelles particules vers ou depuis l'intérieur de l'océan.
ID:(1633, 0)
Mécanismes
Iframe
Mécanismes
ID:(15640, 0)
Couche de surface
Description
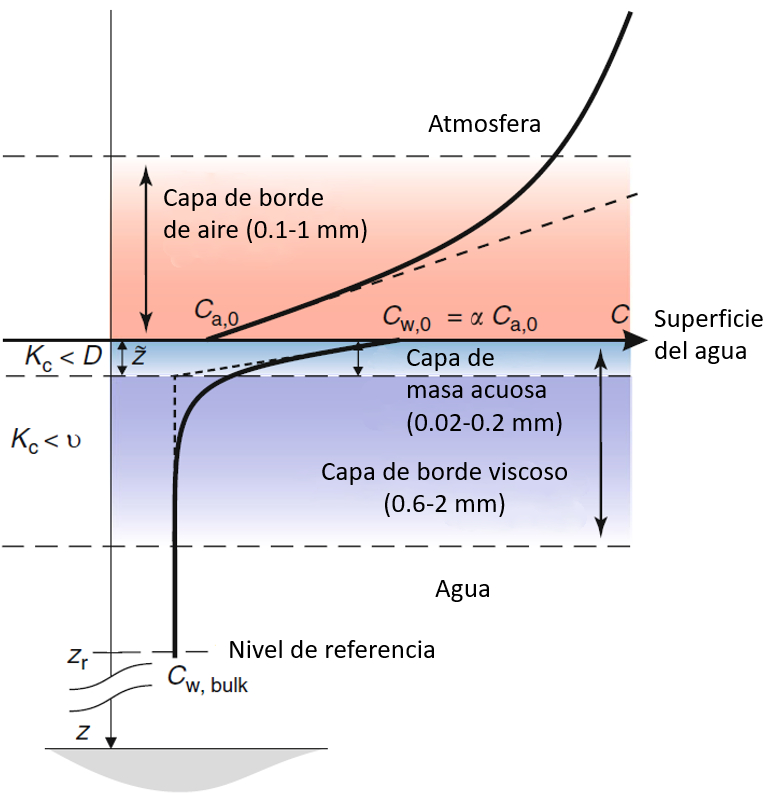
Pour étudier le transfert de CO2 à la surface de l'océan, il est nécessaire d\'observer attentivement les variations de concentration à la fois dans l\'air et dans l\'eau.
Dans l\'air, le CO2 pénètre dans l\'eau, créant une zone de faible concentration où il diminue de $C_a$ à $C_{a,0}$. Cette couche a une épaisseur de 0,1 à 1 mm.
Le CO2 qui pénètre dans l\'eau s\'accumule initialement à la surface, créant une concentration $C_{w,0}$, qui se diffuse ensuite vers l\'intérieur, atteignant une concentration plus faible $C_w$.
La réduction de la concentration permet de définir deux zones : une zone très mince, de 0,02 à 0,2 mm, où la concentration diminue rapidement, et une seconde zone, de 0,6 à 2 mm, où la concentration diminue plus progressivement jusqu\'à atteindre la concentration dans l\'eau.
ID:(12244, 0)
Échange de CO2, vitesse de l'eau
Concept
A taux de transfert de gaz dans l'eau ($k_w$) peut être modélisé en utilisant des données mesurées. Tout d'abord, il dépend de la vitesse à laquelle le système élimine le carbone de l'interface air-eau, ce qui rend la vitesse de transport proportionnelle à la vitesse relative entre les deux milieux.
Deuxièmement, il y a un effet de la mobilité des ions, qui peut être décrit par le numéro de Schmidt ($Sc$), représentant la relation entre la diffusion de l'impulsion et les particules. Cependant, cette dépendance n'est pas linéaire et est influencée par un facteur ($$) qui varie entre -1/2 et -2/3 en fonction de la rugosité de la surface.
Enfin, a taux de transfert de gaz dans l'eau ($k_w$) dépend également de ($$), qui est à son tour déterminé par le niveau de rugosité de la surface.
En résumé, le gaz a taux de transfert de gaz dans l'eau ($k_w$) est décrit en fonction de ($$), ($$), le numéro de Schmidt ($Sc$), ($$) et ($$) de la manière suivante :
| $ k_w = ( u_a - u_w ) \beta Sc ^ n $ |
ID:(15652, 0)
Solubilité en fonction du nombre de Schmidt
Concept
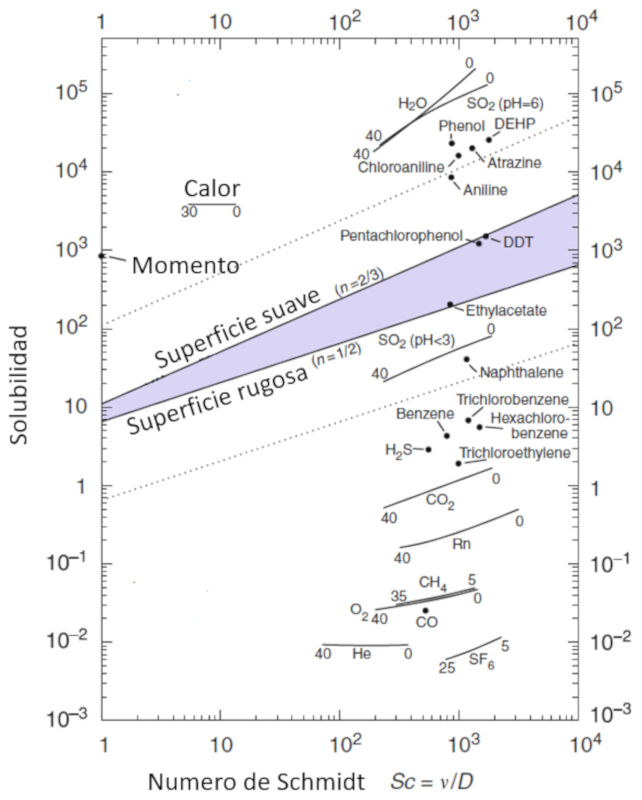
La mobilité des molécules, représentée par a solubilité du gaz ($\alpha$), est une fonction de la concentration de particules, décrite par le numéro de Schmidt ($Sc$), qui à son tour est calculée à partir de ($$), ($$) et ($$) selon l'équation suivante :
| $ Sc =\displaystyle\frac{ \eta }{ \rho D }$ |
Cette relation est illustrée dans le schéma suivant :
ID:(12245, 0)
Vitesse de transfert
Concept
A taux de transfert de gaz dans l'air ($k_a$) peut être estimé à partir de la loi de Fick, en comparant ($$) avec ($$) de la manière suivante :
| $ k_a = \displaystyle\frac{ D }{ \delta_c }$ |
ID:(15653, 0)
Vitesse de transfert et résistances
Concept
Pour l'interaction entre l'atmosphère et l'océan, a résistance au transfert air-eau d'un gaz ($R_{ta}$) comprend initialement a résistance au transfert dans l'eau ($R_w$), suivi du processus d'évaporation $1/\alpha$ avec a solubilité du gaz ($\alpha$), et une fois que le gaz est passé dans l'air, a résistance de transfert dans l'air ($R_a$) agit sur lui :
Quant à l'interaction entre l'atmosphère et l'océan, a résistance au transfert eau-air d'un gaz ($R_{tw}$) comprend initialement a résistance de transfert dans l'air ($R_a$), suivi de a solubilité du gaz ($\alpha$), et une fois que le gaz a pénétré dans l'eau, a résistance au transfert dans l'eau ($R_w$) agit :
Avec ces équations, nous pouvons formuler les équations pour les vitesses de transfert.
Ainsi, en utilisant a taux de transfert total de gaz dans l'air ($k_{ta}$), a taux de transfert de gaz dans l'eau ($k_w$), a taux de transfert de gaz dans l'air ($k_a$) et a solubilité du gaz ($\alpha$), nous établissons la relation suivante :
D'autre part, avec a taux de transfert total de gaz dans l'eau ($k_{tw}$), a taux de transfert de gaz dans l'eau ($k_w$), a taux de transfert de gaz dans l'air ($k_a$) et a solubilité du gaz ($\alpha$), nous établissons que :
ID:(15654, 0)
Modèle
Top
Paramètres
Variables
Calculs
à 
, puis, sélectionnez la variable: 
à 
Calculs
Calculs
Variable 
Donnée Calculer 
Cible : Équation À utiliser 
Équations
$ \displaystyle\frac{1}{ k_{ta} } = \displaystyle\frac{1}{ k_a } + \displaystyle\frac{1}{ \alpha k_w } $
1/ k_ta = 1/ k_a + 1/( k_w * alpha )
$ \displaystyle\frac{1}{ k_{tw} } = \displaystyle\frac{1}{ k_w } + \displaystyle\frac{ \alpha }{ k_a } $
1/ k_tw = 1/ k_w + alpha / k_a
$ C_w = \alpha C_a $
C_w = alpha * C_a
$ k_a = \displaystyle\frac{ D }{ \delta_c }$
k_a = D / delta_c
$ k_w = ( u_a - u_w ) \beta Sc ^ n $
k_w = ( u_a - u_w )* beta * Sc ^ n
$ R_a = \displaystyle\frac{1}{ k_a } $
R_a = 1/ k_a
$ R_{ta} = \displaystyle\frac{1}{ k_{ta} } $
R_ta = 1/ k_ta
$ R_{ta} = R_a + \displaystyle\frac{1}{ \alpha } R_w $
R_ta = R_a + R_w / alpha
$ R_{tw} = \displaystyle\frac{1}{ k_{tw} } $
R_tw = 1/ k_tw
$ R_{tw} = R_w + \alpha R_a $
R_tw = R_w + alpha * R_a
$ R_w = \displaystyle\frac{1}{ k_w } $
R_w = 1/ k_w
ID:(15645, 0)
Relations de concentration de surface
Équation
Le gradient de concentration entre a concentration de gaz dans l'atmosphère ($C_a$) et a concentration de gaz dans l'eau ($C_{w,0}$) dépend de a solubilité du gaz ($\alpha$). Par conséquent, la relation suivante est établie :
| $ C_w = \alpha C_a $ |
ID:(12235, 0)
Vitesse de transfert
Équation
A taux de transfert de gaz dans l'air ($k_a$) peut être estimé à partir de la loi de Fick, en comparant ($$) avec ($$) de la manière suivante :
| $ k_a = \displaystyle\frac{ D }{ \delta_c }$ |
ID:(12227, 0)
Échange de CO2, vitesse de l'eau
Équation
Le paramètre du gaz a taux de transfert de gaz dans l'eau ($k_w$) est décrit en fonction de ($$), ($$), le numéro de Schmidt ($Sc$), ($$) et ($$) comme suit :
| $ k_w = ( u_a - u_w ) \beta Sc ^ n $ |
ID:(12215, 0)
Taux de transfert et résistance dans l'atmosphère
Équation
A résistance de transfert dans l'air ($R_a$) est défini comme l'inverse de a taux de transfert de gaz dans l'air ($k_a$). Cette relation peut être exprimée de la manière suivante :
| $ R_a = \displaystyle\frac{1}{ k_a } $ |
ID:(12236, 0)
Taux de transfert et résistance dans l'océan
Équation
A résistance au transfert dans l'eau ($R_w$) est défini comme l'inverse de a taux de transfert de gaz dans l'eau ($k_w$). Cette relation peut être exprimée de la manière suivante :
| $ R_w = \displaystyle\frac{1}{ k_w } $ |
ID:(12237, 0)
Taux de transfert total atmosphère-océan
Équation
A résistance au transfert eau-air d'un gaz ($R_{tw}$) est défini comme l'inverse de a taux de transfert total de gaz dans l'eau ($k_{tw}$). Cette relation peut être exprimée de la manière suivante :
| $ R_{tw} = \displaystyle\frac{1}{ k_{tw} } $ |
ID:(12238, 0)
Taux de transfert total océan-atmosphère
Équation
A résistance au transfert air-eau d'un gaz ($R_{ta}$) est défini comme l'inverse de a taux de transfert total de gaz dans l'air ($k_{ta}$). Cette relation peut être exprimée de la manière suivante :
| $ R_{ta} = \displaystyle\frac{1}{ k_{ta} } $ |
ID:(12239, 0)
Résistance totale au transfert océan-atmosphère
Équation
Pour l'interaction entre l'atmosphère et l'océan, a résistance au transfert air-eau d'un gaz ($R_{ta}$) inclut d'abord a résistance au transfert dans l'eau ($R_w$), suivi par le processus d'évaporation $1/\alpha$ avec a solubilité du gaz ($\alpha$). Une fois que le gaz est passé dans l'air, a résistance de transfert dans l'air ($R_a$) agit sur lui :
| $ R_{ta} = R_a + \displaystyle\frac{1}{ \alpha } R_w $ |
ID:(12240, 0)
Résistance totale au transfert atmosphère-océan
Équation
Pour l'interaction entre l'atmosphère et l'océan, a résistance au transfert eau-air d'un gaz ($R_{tw}$) inclut d'abord a résistance de transfert dans l'air ($R_a$), suivi par a solubilité du gaz ($\alpha$). Une fois que le gaz a pénétré dans l'eau, a résistance au transfert dans l'eau ($R_w$) agit :
| $ R_{tw} = R_w + \alpha R_a $ |
ID:(12241, 0)
Taux de transfert atmosphère-océan
Équation
La relation entre la résistance au transfert entre l'atmosphère et l'océan peut être exprimée en termes des vitesses de transfert dans les deux milieux, équivalant à l'inverse de la vitesse de transfert totale.
Ainsi, avec a taux de transfert total de gaz dans l'eau ($k_{tw}$), a taux de transfert de gaz dans l'eau ($k_w$), a taux de transfert de gaz dans l'air ($k_a$) et a solubilité du gaz ($\alpha$), il est établi que :
| $ \displaystyle\frac{1}{ k_{tw} } = \displaystyle\frac{1}{ k_w } + \displaystyle\frac{ \alpha }{ k_a } $ |
La relation entre a résistance au transfert eau-air d'un gaz ($R_{tw}$), établie par les sommes de a résistance au transfert dans l'eau ($R_w$), a résistance de transfert dans l'air ($R_a$) et a solubilité du gaz ($\alpha$), est exprimée dans l'équation :
| $ R_{tw} = R_w + \alpha R_a $ |
Incluant la relation de a résistance de transfert dans l'air ($R_a$) avec a taux de transfert de gaz dans l'air ($k_a$) dans :
| $ R_a = \displaystyle\frac{1}{ k_a } $ |
L'interaction de a résistance au transfert dans l'eau ($R_w$) avec a taux de transfert de gaz dans l'eau ($k_w$) est décrite dans :
| $ R_w = \displaystyle\frac{1}{ k_w } $ |
Et la connexion entre a résistance au transfert eau-air d'un gaz ($R_{tw}$) et a taux de transfert total de gaz dans l'eau ($k_{tw}$) est détaillée dans :
| $ R_{tw} = \displaystyle\frac{1}{ k_{tw} } $ |
Ceci fournit la base pour établir la relation pour a taux de transfert total de gaz dans l'eau ($k_{tw}$) :
| $ \displaystyle\frac{1}{ k_{tw} } = \displaystyle\frac{1}{ k_w } + \displaystyle\frac{ \alpha }{ k_a } $ |
ID:(12243, 0)
Taux de transfert océan-atmosphère
Équation
La relation de la résistance au transfert entre l'océan et l'atmosphère peut être exprimée en termes des vitesses de transfert dans les deux milieux, correspondant à l'inverse de la vitesse totale de transfert.
Ainsi, en utilisant a taux de transfert total de gaz dans l'air ($k_{ta}$), a taux de transfert de gaz dans l'eau ($k_w$), a taux de transfert de gaz dans l'air ($k_a$) et a solubilité du gaz ($\alpha$), la relation suivante est établie :
| $ \displaystyle\frac{1}{ k_{ta} } = \displaystyle\frac{1}{ k_a } + \displaystyle\frac{1}{ \alpha k_w } $ |
La relation impliquant a résistance au transfert air-eau d'un gaz ($R_{ta}$), déterminée par la combinaison de a résistance au transfert dans l'eau ($R_w$), a résistance de transfert dans l'air ($R_a$) et a solubilité du gaz ($\alpha$), est formulée dans l'équation :
| $ R_{ta} = R_a + \displaystyle\frac{1}{ \alpha } R_w $ |
Cela inclut la relation de a résistance de transfert dans l'air ($R_a$) avec a taux de transfert de gaz dans l'air ($k_a$) exprimée dans :
| $ R_a = \displaystyle\frac{1}{ k_a } $ |
De plus, l'interaction de a résistance au transfert dans l'eau ($R_w$) avec a taux de transfert de gaz dans l'eau ($k_w$) est expliquée dans :
| $ R_w = \displaystyle\frac{1}{ k_w } $ |
Et la connexion entre a résistance au transfert air-eau d'un gaz ($R_{ta}$) et a taux de transfert total de gaz dans l'air ($k_{ta}$) est spécifiée dans :
| $ R_{ta} = \displaystyle\frac{1}{ k_{ta} } $ |
Ces éléments ensemble fournissent la base pour définir la relation pour a taux de transfert total de gaz dans l'air ($k_{ta}$) :
| $ \displaystyle\frac{1}{ k_{ta} } = \displaystyle\frac{1}{ k_a } + \displaystyle\frac{1}{ \alpha k_w } $ |
ID:(12242, 0)