User:
Particle exchange
Storyboard 
The exchange of substances between the atmosphere and the ocean can include particles. This is particularly relevant when studying the transfer of CO2 molecules from the atmosphere to the ocean.
Ocean-Atmosphere Interactions of Gases and Particles, Peter S. Liss, Martin T. Johnson (eds.). Springer, 2014
Chapter: Transfer Across the Air-Sea Interface
ID:(1630, 0)
CO2 diffusion
Description
The absorption of CO2 by the oceans helps mitigate the effects of this gas in the atmosphere and therefore delays climate change. However, the processes involved are more complex and include:
- Gas exchange with the atmosphere: The ocean and the atmosphere are in constant exchange of CO2 through gas diffusion. Atmospheric CO2 dissolves in the surface of the ocean and forms carbonic acid (H2CO3), which then dissociates into hydrogen ions (H+) and bicarbonate ions (HCO3-). This process helps balance the CO2 levels between the ocean and the atmosphere.
- Photosynthesis and respiration: Marine organisms, such as phytoplankton and algae, perform photosynthesis and take up CO2 from the water to produce organic matter and release oxygen. This process, known as carbon fixation, helps extract CO2 from the ocean. On the other hand, marine organisms also respire, which means they release CO2 into the water during the decomposition of organic matter.
- Ocean circulation: The ocean is characterized by its global circulation, in which currents transport CO2-rich water from the surface to the depths and vice versa. This contributes to the distribution and mixing of CO2 throughout the ocean, allowing deep waters to store large amounts of dissolved CO2.
- Sedimentation and burial: Part of the organic matter produced by marine organisms, including CO2 captured through photosynthesis, can sink to the ocean floor. As sediments accumulate over geological time, the organic carbon can become buried and stored in the seafloor for long periods.
Annual carbon flux in PgC/yr. Numbers in black are pre-industrial revolution, in red are increases related to the industrial revolution. Ocean-Atmosphere Interactions of Gases and Particles, Peter S. Liss Martin T. Johnson (Editors), Springer, 2014
Depending on the area and time of the planet, there is a greater concentration of carbon in the atmosphere than in the ocean or vice versa, thus defining whether the flow of carbon is from air to water or vice versa.
ID:(12297, 0)
Transfer rate and relative speed
Description
In a first approximation, the dependence of the gas transfer rate in water ($k_w$) in relation to the relative velocity, calculated by subtracting the velocidad del agua ($u_w$) from the velocidad del aire ($u_a$), is proportional to
$k_w \propto u_a - u_w$
as observed in the graph:
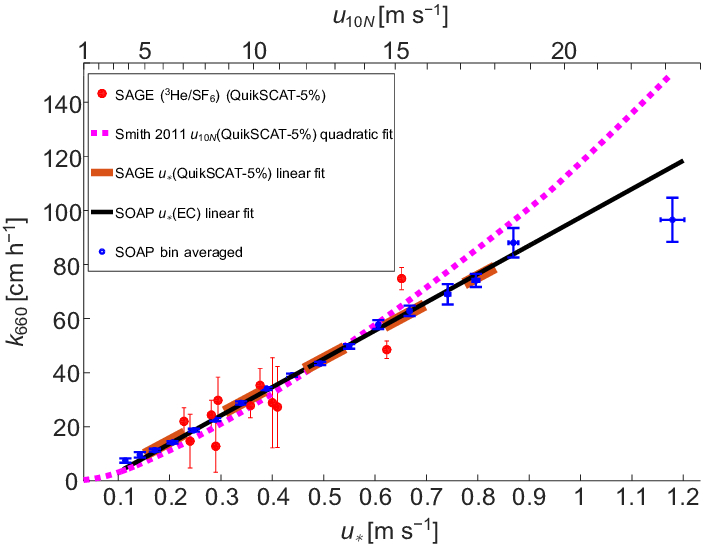
ID:(12298, 0)
Transfer rate and Schmidt number
Description
The relationship between the gas transfer rate in water ($k_w$) is inversely proportional to the schmidt number ($Sc$), so it is expressed as proportional to that number raised to exponente de Schmidt ($n$), which is negative:
$k_w\propto Sc^n$
which is represented with exponente de Schmidt ($n$) equal to -0.5:
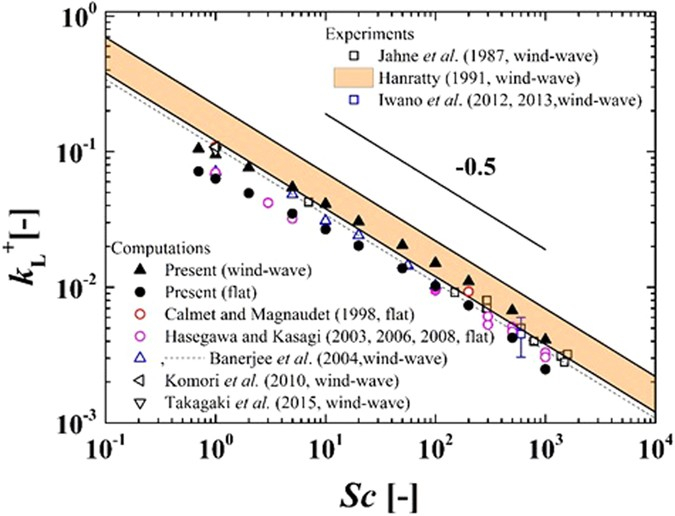
ID:(12299, 0)
Solubility as a function of Schmidt number
Concept
The mobility of molecules, represented by the gas solubility ($\alpha$), is modeled as a function of particle concentration, characterized by the schmidt number ($Sc$), which in turn is calculated from parameters the viscosidad en masa acuosa ($\eta$), the densidad en capa de masa acuosa ($\rho$), and the constante de difusión en masa acuosa ($D$) using the following expression:
| $ Sc =\displaystyle\frac{ \eta }{ \rho D }$ |
This relationship is visualized in the following diagram:
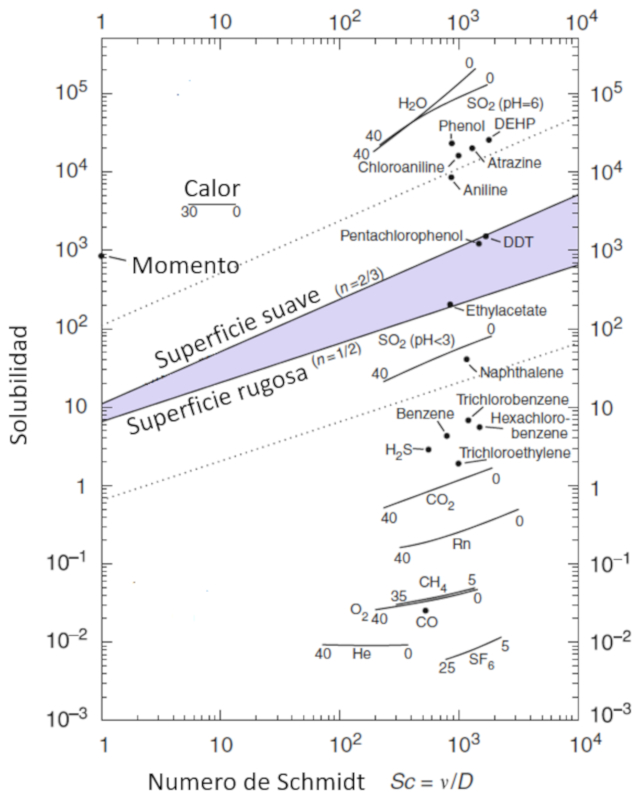
Ocean-Atmosphere Interactions of Gases and Particles, Peter S. Liss, Martin T. Johnson (eds.), Springer-Verlag Berlin Heidelberg
ID:(12245, 0)
CO2 exchange, speed from water
Concept
The gas transfer rate in water ($k_w$) can be modeled using measured data. Firstly, it depends on the rate at which the system removes carbon from the air-water interface, making the transport speed proportional to the relative velocity between the two mediums.
Secondly, there is an effect of ion mobility, which can be described by the schmidt number ($Sc$), representing the relationship between momentum diffusion and particles. However, this dependence is not linear and is influenced by a factor exponente de Schmidt ($n$) that varies between -1/2 and -2/3 depending on the surface roughness.
Finally, the gas transfer rate in water ($k_w$) also depends on the factor beta del transporte aire a agua de CO2 ($\beta$), which in turn is determined by the level of surface roughness.
In summary, the gas the gas transfer rate in water ($k_w$) is described as a function of the velocidad del agua ($u_w$), the velocidad del aire ($u_a$), the schmidt number ($Sc$), the factor beta del transporte aire a agua de CO2 ($\beta$), and exponente de Schmidt ($n$) as follows:
| $ k_w = ( u_a - u_w ) \beta Sc ^ n $ |
ID:(15652, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ C = D_C U_z ( C_z - C_0 )$
C = D_C * U_z *( C_z - C_0 )
$ C_w = \alpha C_a $
C_w = alpha * C_a
$ \delta_c = \sqrt{\displaystyle\frac{ \rho D }{ \eta }} \delta_{\eta}$
delta_c =sqrt( D * rho / eta )* delta_eta
$ F_a =- k_a \Delta p_{gas} $
F_a =- k_a * Dp_gas
$ F_w = k_w \Delta p_{gas} $
F_w = k_w * Dp_gas
$ k =\displaystyle\frac{ F }{ C_0 - C_b }$
k = F /( C_0 - C_b )
$ k_a = \displaystyle\frac{ D }{ \delta_c }$
k_a = D / delta_c
$ k_w = ( u_a - u_w ) \beta Sc ^ n $
k_w = ( u_a - u_w )* beta * Sc ^ n
$ Sc =\displaystyle\frac{ \eta }{ \rho D }$
Sc = eta /( rho * D )
ID:(15641, 0)
Diffusive flux with the transfer velocity
Equation
Since the diffusive flux $F$ can be modeled using Fick\'s law:
| $ F = - D \displaystyle\frac{d C }{d t }$ |
We can establish a relationship between the transfer velocity $k$ and the concentration difference $\Delta C$ as follows:
| $ F_a =- k_a \Delta p_{gas} $ |
The diffusive flux $F$ is described by Fick\'s law:
| $ F = - D \displaystyle\frac{d C }{d t }$ |
where $D$ is the diffusion constant and $dC/dx$ is the concentration gradient. By defining a transfer velocity as:
| $ k_a = \displaystyle\frac{ D }{ \delta_c }$ |
we can establish a flow equation of the form:
| $ F_a =- k_a \Delta p_{gas} $ |
ID:(12226, 0)
Concentration profile in the surface layer (MOST)
Equation
Using the Monin-Obukhov Similarity Theory (MOST) model, the flux of elements such as gases can be estimated by considering the displacement of the surface and a transfer coefficient, which is expressed as follows:
| $ C = D_C U_z ( C_z - C_0 )$ |
In the Monin-Obukhov Similarity Theory (MOST) model, the flux of elements such as gases is estimated by considering the difference in concentrations between the air and water, represented by
$C_z - C_0$
and the flux is calculated using the transfer coefficient $D_C$ and the surface velocity $U_z$, as follows:
| $ C = D_C U_z ( C_z - C_0 )$ |
This allows for the estimation of the flux of elements between the air and water.
ID:(12224, 0)
Surface Concentration Relationships
Equation
The concentration gradient between the gas concentration in the atmosphere ($C_a$) and the gas concentration in water ($C_{w,0}$) depends on the gas solubility ($\alpha$). Therefore, the following relationship is established:
| $ C_w = \alpha C_a $ |
ID:(12235, 0)
Transport of a quantity
Equation
The transfer velocity of a quantity $k$ is defined as the flux $F$ divided by the concentration difference between the two media, represented by
$C_0-C_b$
Therefore, it can be expressed as:
| $ k =\displaystyle\frac{ F }{ C_0 - C_b }$ |
ID:(12213, 0)
Transfer speed
Equation
The gas transfer rate in air ($k_a$) can be estimated from Fick's law by comparing the constante de difusión en masa acuosa ($D$) with the grosor de la capa superficial ($\delta_c$) as follows:
| $ k_a = \displaystyle\frac{ D }{ \delta_c }$ |
ID:(12227, 0)
CO2 exchange
Equation
The transfer rate of CO2 from the atmosphere to water can be modeled using an equation similar to the general rule
| $ k =\displaystyle\frac{ F }{ C_0 - C_b }$ |
In this model, the concentration difference is replaced by the difference in partial pressure of the gas and its solubility $\alpha$. The equation can be expressed as:
| $ F_w = k_w \Delta p_{gas} $ |
If we consider the gas flux as $F$ and the transport velocity as $k$, according to the general relationship:
| $ k =\displaystyle\frac{ F }{ C_0 - C_b }$ |
By replacing the concentration difference $C_0 - C_b$ with the difference in partial pressure of the gas using the solubility $\alpha$, we have:
$C_0 - C_b = \alpha \Delta p_{CO2}$
we can obtain:
| $ F_w = k_w \Delta p_{gas} $ |
ID:(12214, 0)
CO2 exchange, speed from water
Equation
The gas parameter the gas transfer rate in water ($k_w$) is described in terms of the velocidad del agua ($u_w$), the velocidad del aire ($u_a$), the schmidt number ($Sc$), the factor beta del transporte aire a agua de CO2 ($\beta$), and exponente de Schmidt ($n$) as follows:
| $ k_w = ( u_a - u_w ) \beta Sc ^ n $ |
ID:(12215, 0)
Schmidt\'s number Sc
Equation
The Schmidt number establishes a relationship between viscous diffusion
| $ D_p \equiv \displaystyle\frac{ \eta }{ \rho }$ |
and particle diffusion
| $ D_N \equiv \mu k_B T $ |
.
The former is equal to viscosity divided by density, while the latter corresponds to the diffusion constant. Therefore, it is defined as follows:
| $ Sc =\displaystyle\frac{ \eta }{ \rho D }$ |
ID:(12216, 0)
Surface thickness and viscous layer
Equation
El grosor de la superficie y de la capa viscosas son proposicionales siendo la constante una función de la constante difusión, viscosidad y densidad.
Por ello con es
| $ \delta_c = \sqrt{\displaystyle\frac{ \rho D }{ \eta }} \delta_{\eta}$ |
ID:(12229, 0)