User:
Breaking waves
Storyboard 
The air currents over the ocean drive the movement of the water, generating waves that behave differently under fluctuations depending on the depth. This phenomenon is known as wave breaking. Wave breaking occurs because the propagation speed of a wave is greater in areas of deeper water. Thus, as waves approach the shore, those from deeper areas tend to overtake those from shallower areas, resulting in the characteristic breaking of the wave.
ID:(1632, 0)
Mechanisms
Iframe
Mechanisms
ID:(15639, 0)
Break of the wave on the beach
Description
When a wave reaches the shore, it starts to climb up the beach slope, becoming progressively shallower and slower. A following wave tends to rise over the preceding wave. As the water becomes deeper in this situation, it becomes faster and tends to overtake the previously arrived water. This interaction ultimately leads to the wave breaking, creating the phenomenon known as surf.
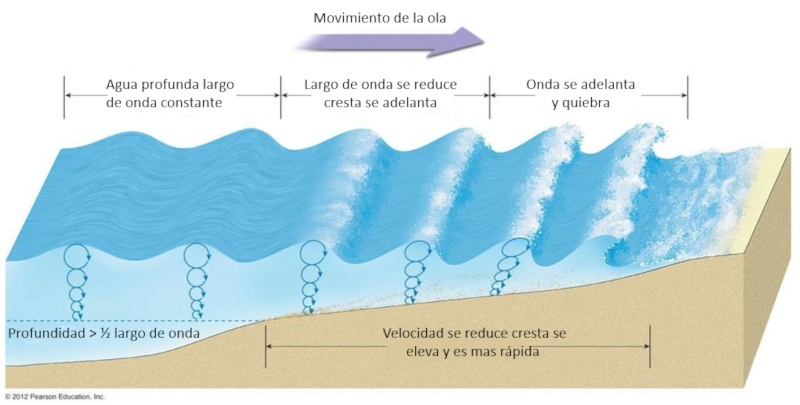
ID:(12308, 0)
Angular frequency
Concept
Recalling that angular velocity represents the angle traversed per unit of time, it can be observed that the expression
$\displaystyle\frac{2\pi}{T}$
corresponds to a complete revolution ($2\pi$) divided by the time the period ($T$), which is required for one cycle. Therefore, the angular frequency ($\omega$) is defined as
| $ \omega = \displaystyle\frac{2 \pi }{ T }$ |
ID:(15648, 0)
Wave vector
Concept
The wave vector ($k$) is the factor that multiplies the position and corresponds to the value for which, if the wave moves along a wave length ($\lambda$), it assumes the same shape it initially had. For this to occur, the following condition must be met:
$kx = k\lambda = 2\pi$
Therefore, with the wave length ($\lambda$), we establish that:
| $ k =\displaystyle\frac{2 \pi }{ \lambda }$ |
ID:(15647, 0)
Wave phase velocity
Concept
The speed of waves depends on the water depth and the factor the wave vector ($k$), which is calculated using the wave length ($\lambda$) as follows:
| $ k =\displaystyle\frac{2 \pi }{ \lambda }$ |
Regarding the phase speed ($c_p$), which corresponds to the speed at which each wave crest moves, this can be determined using the ocean depth ($h$) and the gravitational Acceleration ($g$). The phase speed ($c_p$) is calculated as:
| $ c_p =\sqrt{\displaystyle\frac{ g }{ k } \tanh( k h )}$ |
The phase velocity refers to the speed at which a specific oscillation or wave moves.
ID:(15649, 0)
Wave group velocity
Concept
Waves have a speed that depends on the water depth and the factor the wave vector ($k$), calculated using the wave length ($\lambda$) as follows:
| $ k =\displaystyle\frac{2 \pi }{ \lambda }$ |
For the group speed ($c_g$), which represents the speed at which the entire wave train moves, not each individual wave, it can be calculated using the phase speed ($c_p$). This is determined with the ocean depth ($h$) and the gravitational Acceleration ($g$), in the following way:
| $ c_p =\sqrt{\displaystyle\frac{ g }{ k } \tanh( k h )}$ |
Finally, using this information, the group speed ($c_g$) can be calculated through the following expression:
| $ c_g =\displaystyle\frac{ c_p }{2}\left(1 + \displaystyle\frac{2 k h }{\sinh(2 k h )}\right)$ |
The group velocity is the speed at which the train or group of waves moves through the water medium.
ID:(15650, 0)
Wave speeds
Image
There are two characteristic speeds in wave mechanics. On one hand, there is the speed at which a specific wave travels, which can vary based on frequency, thus differing from one wave to another.
The second type of speed observed is that of a wave packet, that is, a group of waves of different frequencies and phases which, when superimposed, form a group that moves as a unit. This speed is known as the group velocity.
Both can be observed in this animation:
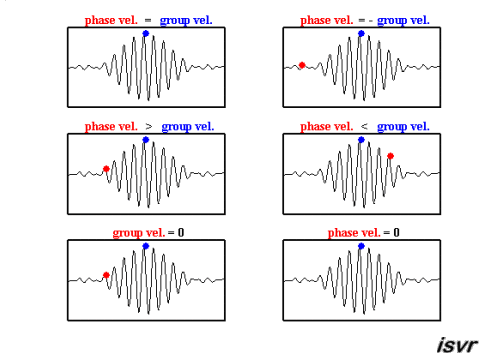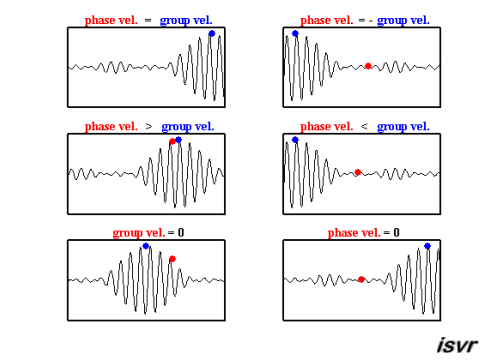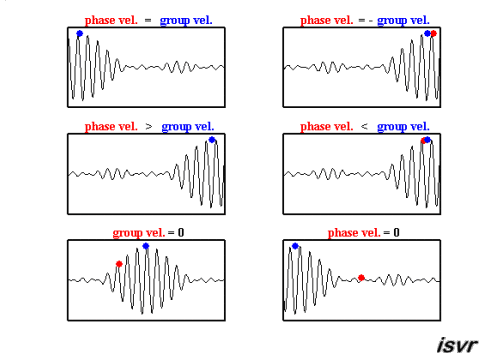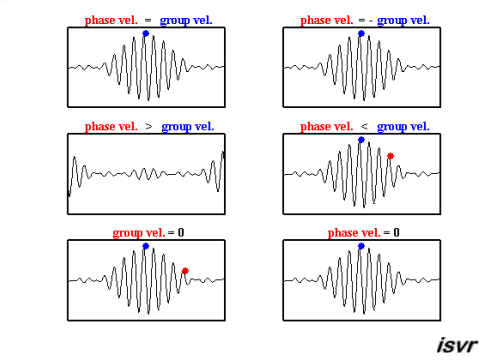
ID:(15651, 0)
Wave description
Concept
A wave can be approximately described as a sinusoidal function depending on the variables the position ($x$) and the time ($t$).
The function incorporates the values of the wave height ($z$) at each point, as well as the maximum wave height ($z_0$), the wave vector ($k$), and the frecuencia angular ($\omega$):
| $ z ( x , t ) = z_0 sin( k x - \omega t )$ |
ID:(15646, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ c_g =\displaystyle\frac{ c_p }{2}\left(1 + \displaystyle\frac{2 k h }{\sinh(2 k h )}\right)$
c_g = c_p*(1 + 2* k * h / sinh( 2 * k * h ))/2
$ c_p =\sqrt{\displaystyle\frac{ g }{ k } \tanh( k h )}$
c_p =sqrt( g * tanh( k * h ) / k )
$ k =\displaystyle\frac{2 \pi }{ \lambda }$
k = 2* pi / lambda
$ \omega = \displaystyle\frac{2 \pi }{ T }$
omega = 2* pi / T
$ z ( x , t ) = z_0 sin( k x - \omega t )$
z_xt = z_0 *sin( k * x - omega * t )
ID:(15644, 0)
Wave description
Equation
A wave can be approximately described as a sinusoidal function depending on the variables the position ($x$) and the time ($t$).
The function incorporates the values of the wave height ($z$) at each point, as well as the maximum wave height ($z_0$), the wave vector ($k$), and the frecuencia angular ($\omega$):
| $ z ( x , t ) = z_0 sin( k x - \omega t )$ |
ID:(12307, 0)
Wave vector
Equation
The wave vector ($k$) is with the wave length ($\lambda$) equal to:
| $ k =\displaystyle\frac{2 \pi }{ \lambda }$ |
ID:(12309, 0)
Angular frequency
Equation
The angular frequency ($\omega$) is with the period ($T$) equal to
| $ \omega = \displaystyle\frac{2 \pi }{ T }$ |
ID:(12335, 0)
Wave phase velocity
Equation
The phase speed ($c_p$) corresponds to the speed at which each wave crest moves, which can be determined using the values the ocean depth ($h$), the wave length ($\lambda$), and the gravitational Acceleration ($g$). The speed the phase speed ($c_p$) is calculated as follows:
| $ c_p =\sqrt{\displaystyle\frac{ g }{ k } \tanh( k h )}$ |
ID:(12305, 0)
Wave group velocity
Equation
The group speed ($c_g$) is calculated using the values of the wave vector ($k$), the ocean depth ($h$), and the gravitational Acceleration ($g$) as follows:
| $ c_g =\displaystyle\frac{ c_p }{2}\left(1 + \displaystyle\frac{2 k h }{\sinh(2 k h )}\right)$ |
ID:(12304, 0)