Storyboard

A transferência de partículas ou moléculas, como o CO2, entre a atmosfera e o oceano envolve um mecanismo mais complexo. Este processo está associado à formação de um filme líquido saturado com partículas ou moléculas, que regula o movimento de novas partículas para dentro ou para fora do interior do oceano.

>Modelo

ID:(1633, 0)

Iframe

>Top

ID:(15640, 0)

Descrição

>Top

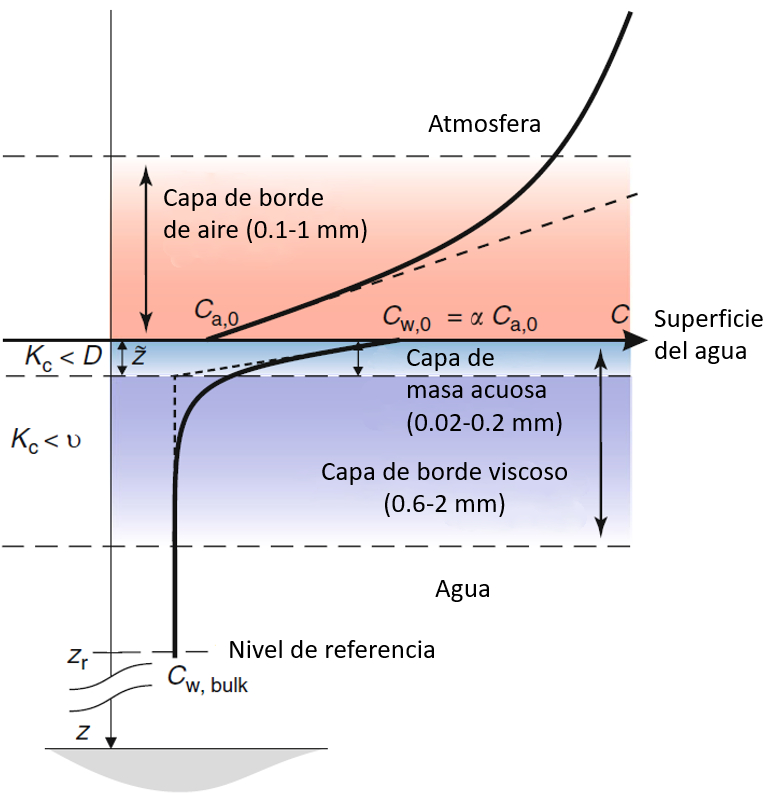
Para estudar a transferência de CO2 na superfície do oceano, é necessário observar em detalhes o que acontece com as concentrações tanto no ar como na água.

No ar, o CO2 entra na água criando uma região de baixa concentração, onde diminui de $C_a$ para $C_{a,0}$. Essa camada tem uma espessura entre 0,1 e 1 mm.

O CO2 que entra na água se acumula inicialmente na superfície, criando uma concentração $C_{w,0}$, que posteriormente difunde para o interior, alcançando uma concentração menor $C_w$.

A redução da concentração permite definir duas zonas: uma muito fina, de apenas 0,02 a 0,2 mm, onde a concentração diminui rapidamente, e uma segunda zona de 0,6 a 2 mm, onde a concentração diminui de forma mais suave até atingir a concentração no interior da água.

ID:(12244, 0)

Conceito

>Top

La taxa de transferência de gás na água ($k_w$) pode ser modelada usando dados medidos. Em primeiro lugar, depende da velocidade com que o sistema remove carbono da interface ar-água, tornando a velocidade de transporte proporcional à velocidade relativa entre os dois meios.

Em segundo lugar, há um efeito da mobilidade dos íons, que pode ser descrito por o número Schmidt ($Sc$), representando a relação entre a difusão de momento e as partículas. No entanto, essa dependência não é linear e é influenciada por um fator ($$) que varia entre -1/2 e -2/3 dependendo da rugosidade da superfície.

Finalmente, la taxa de transferência de gás na água ($k_w$) também depende de ($$), que por sua vez é determinada pelo nível de rugosidade da superfície.

Em resumo, o gás la taxa de transferência de gás na água ($k_w$) é descrito em função de ($$), ($$), o número Schmidt ($Sc$), ($$) e ($$) da seguinte maneira:

ID:(15652, 0)

Conceito

>Top

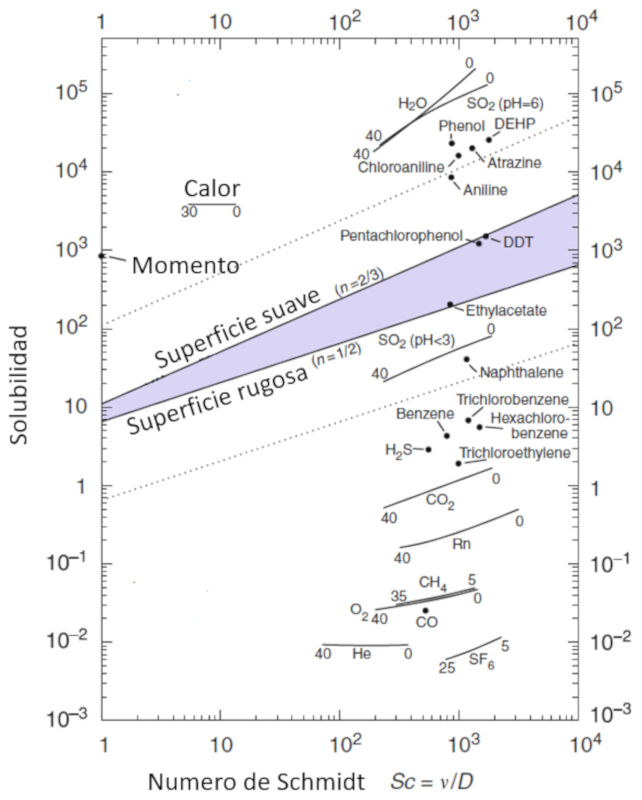
A mobilidade das moléculas, representada por la solubilidade de gás ($\alpha$), é uma função da concentração de partículas, descrita por o número Schmidt ($Sc$), que por sua vez é calculada a partir de ($$), ($$) e ($$) utilizando a seguinte equação:

Essa relação é ilustrada no seguinte diagrama:

ID:(12245, 0)

Conceito

>Top

La taxa de transferência de gás no ar ($k_a$) pode ser estimado a partir da lei de Fick, comparando ($$) com ($$) da seguinte maneira:

ID:(15653, 0)

Conceito

>Top

Para a interação entre a atmosfera e o oceano, la resistência à transferência de ar para água de um gás ($R_{ta}$) inclui inicialmente la resistência à transferência na água ($R_w$), seguido pelo processo de evaporação $1/\alpha$ com la solubilidade de gás ($\alpha$), e, uma vez que o gás tenha passado para o ar, la resistência de transferência no ar ($R_a$) age sobre ele:

Já para a interação entre a atmosfera e o oceano, la resistência à transferência de água para ar de um gás ($R_{tw}$) inclui inicialmente la resistência de transferência no ar ($R_a$), seguido de la solubilidade de gás ($\alpha$), e, uma vez que o gás tenha penetrado na água, age la resistência à transferência na água ($R_w$):

Com essas equações, podemos formular as equações para as velocidades de transferência.

Assim, utilizando la taxa total de transferência de gás no ar ($k_{ta}$), la taxa de transferência de gás na água ($k_w$), la taxa de transferência de gás no ar ($k_a$) e la solubilidade de gás ($\alpha$), estabelecemos a seguinte relação:

Por outro lado, com la taxa total de transferência de gás na água ($k_{tw}$), la taxa de transferência de gás na água ($k_w$), la taxa de transferência de gás no ar ($k_a$) e la solubilidade de gás ($\alpha$), estabelecemos que:

ID:(15654, 0)

Top

>Top

Parâmetros

$Sc$

Sc

Número Schmidt

-

$\alpha$

alpha

Solubilidade de gás

-

$k_a$

k_a

Taxa de transferência de gás no ar

m/s

Variáveis

$C_{w,0}$

C_w0

Concentração de gás na água

1/m^3

$C_a$

C_a

Concentração de gás na atmosfera

1/m^3

$R_{tw}$

R_tw

Resistência à transferência de água para ar de um gás

s/m

$R_{ta}$

R_ta

Resistência à transferência de ar para água de um gás

s/m

$R_w$

R_w

Resistência à transferência na água

s/m

$R_a$

R_a

Resistência de transferência no ar

s/m

$k_w$

k_w

Taxa de transferência de gás na água

m/s

$k_{tw}$

k_tw

Taxa total de transferência de gás na água

m/s

$k_{ta}$

k_ta

Taxa total de transferência de gás no ar

m/s

Cálculos

• Método alternativo
• Método tradicional
• Estratégia
• 2D
• 3D

Equação

Equação

Primeiro, selecione a equação: para , depois, selecione a variável: para

---

Cálculos

Símbolo

Equação

Resolvido

Traduzido

Cálculos

Símbolo

Equação

Resolvido

Traduzido

Variáve Dado Calcular Objetivo : Equação A ser usado

Equações

ID:(15645, 0)

Equação

>Top, >Modelo

O gradiente de concentração entre la concentração de gás na atmosfera ($C_a$) e la concentração de gás na água ($C_{w,0}$) depende de la solubilidade de gás ($\alpha$). Portanto, estabelece-se a seguinte relação:

$C_w = \alpha C_a$

Condições

Variáveis

$C_w$

Concentração de gás na água

$1/m^3$

9415

$C_a$

Concentração de gás na atmosfera

$1/m^3$

9416

$\alpha$

Solubilidade de gás

$-$

9406

Relação

ID:(12235, 0)

Equação

>Top, >Modelo

La taxa de transferência de gás no ar ($k_a$) pode ser estimado a partir da lei de Fick, comparando ($$) com ($$) da seguinte maneira:

$k_a = \displaystyle\frac{ D }{ \delta_c }$

Condições

Variáveis

$k_a$

Taxa de transferência de gás no ar

$m/s$

9407

Relação

ID:(12227, 0)

Equação

>Top, >Modelo

O parâmetro do gás la taxa de transferência de gás na água ($k_w$) é descrito em termos de ($$), ($$), o número Schmidt ($Sc$), ($$) e ($$) da seguinte forma:

$k_w = ( u_a - u_w ) \beta Sc ^ n$

Condições

Variáveis

$Sc$

Número Schmidt

$-$

9410

$k_w$

Taxa de transferência de gás na água

$m/s$

9405

Relação

ID:(12215, 0)

Equação

>Top, >Modelo

La resistência de transferência no ar ($R_a$) é definido como o inverso de la taxa de transferência de gás no ar ($k_a$). Esta relação pode ser expressa da seguinte maneira:

$R_a = \displaystyle\frac{1}{ k_a }$

Condições

Variáveis

$R_a$

Resistência de transferência no ar

$s/m$

9443

$k_a$

Taxa de transferência de gás no ar

$m/s$

9407

Relação

ID:(12236, 0)

Equação

>Top, >Modelo

La resistência à transferência na água ($R_w$) é definido como o inverso de la taxa de transferência de gás na água ($k_w$). Esta relação pode ser expressa da seguinte maneira:

$R_w = \displaystyle\frac{1}{ k_w }$

Condições

Variáveis

$R_w$

Resistência à transferência na água

$s/m$

9444

$k_w$

Taxa de transferência de gás na água

$m/s$

9405

Relação

ID:(12237, 0)

Equação

>Top, >Modelo

La resistência à transferência de água para ar de um gás ($R_{tw}$) wird als das Inverse von la taxa total de transferência de gás na água ($k_{tw}$) definiert. Diese Beziehung kann wie folgt ausgedrückt werden:

$R_{tw} = \displaystyle\frac{1}{ k_{tw} }$

Condições

Variáveis

$R_{tw}$

Resistência à transferência de água para ar de um gás

$s/m$

9446

$k_{tw}$

Taxa total de transferência de gás na água

$m/s$

9448

Relação

ID:(12238, 0)

Equação

>Top, >Modelo

La resistência à transferência de ar para água de um gás ($R_{ta}$) é definido como o inverso de la taxa total de transferência de gás no ar ($k_{ta}$). Esta relação pode ser expressa da seguinte maneira:

$R_{ta} = \displaystyle\frac{1}{ k_{ta} }$

Condições

Variáveis

$R_{ta}$

Resistência à transferência de ar para água de um gás

$s/m$

9445

$k_{ta}$

Taxa total de transferência de gás no ar

$m/s$

9447

Relação

ID:(12239, 0)

Equação

>Top, >Modelo

Para a interação entre a atmosfera e o oceano, la resistência à transferência de ar para água de um gás ($R_{ta}$) inclui inicialmente la resistência à transferência na água ($R_w$), seguido pelo processo de evaporação $1/\alpha$ com la solubilidade de gás ($\alpha$). Uma vez que o gás tenha sido transferido para o ar, la resistência de transferência no ar ($R_a$) atua sobre ele:

$R_{ta} = R_a + \displaystyle\frac{1}{ \alpha } R_w$

Condições

Variáveis

$R_{ta}$

Resistência à transferência de ar para água de um gás

$s/m$

9445

$R_w$

Resistência à transferência na água

$s/m$

9444

$R_a$

Resistência de transferência no ar

$s/m$

9443

$\alpha$

Solubilidade de gás

$-$

9406

Relação

ID:(12240, 0)

Equação

>Top, >Modelo

Para a interação entre a atmosfera e o oceano, la resistência à transferência de água para ar de um gás ($R_{tw}$) inclui inicialmente la resistência de transferência no ar ($R_a$), seguido por la solubilidade de gás ($\alpha$). Uma vez que o gás tenha penetrado na água, la resistência à transferência na água ($R_w$) atua:

$R_{tw} = R_w + \alpha R_a$

Condições

Variáveis

$R_{tw}$

Resistência à transferência de água para ar de um gás

$s/m$

9446

$R_w$

Resistência à transferência na água

$s/m$

9444

$R_a$

Resistência de transferência no ar

$s/m$

9443

$\alpha$

Solubilidade de gás

$-$

9406

Relação

ID:(12241, 0)

Equação

>Top, >Modelo

A relação entre a resistência de transferência entre a atmosfera e o oceano pode ser expressa em termos das velocidades de transferência em ambos os meios, equivalendo ao inverso da velocidade de transferência total.

Portanto, com la taxa total de transferência de gás na água ($k_{tw}$), la taxa de transferência de gás na água ($k_w$), la taxa de transferência de gás no ar ($k_a$) e la solubilidade de gás ($\alpha$), estabelece-se que:

$\displaystyle\frac{1}{ k_{tw} } = \displaystyle\frac{1}{ k_w } + \displaystyle\frac{ \alpha }{ k_a }$

Condições

Variáveis

$\alpha$

Solubilidade de gás

$-$

9406

$k_w$

Taxa de transferência de gás na água

$m/s$

9405

$k_a$

Taxa de transferência de gás no ar

$m/s$

9407

$k_{tw}$

Taxa total de transferência de gás na água

$m/s$

9448

Relação

Desenvolvimento

A relação entre la resistência à transferência de água para ar de um gás ($R_{tw}$), estabelecida através das somas de la resistência à transferência na água ($R_w$), la resistência de transferência no ar ($R_a$) e la solubilidade de gás ($\alpha$), é expressa na equação:

$R_{tw} = R_w + \alpha R_a$

Incluindo a relação de la resistência de transferência no ar ($R_a$) com la taxa de transferência de gás no ar ($k_a$) em:

$R_a = \displaystyle\frac{1}{ k_a }$

A interação de la resistência à transferência na água ($R_w$) com la taxa de transferência de gás na água ($k_w$) é descrita em:

$R_w = \displaystyle\frac{1}{ k_w }$

E a conexão entre la resistência à transferência de água para ar de um gás ($R_{tw}$) e la taxa total de transferência de gás na água ($k_{tw}$) é detalhada em:

$R_{tw} = \displaystyle\frac{1}{ k_{tw} }$

Isso fornece a base para estabelecer a relação para la taxa total de transferência de gás na água ($k_{tw}$):

$\displaystyle\frac{1}{ k_{tw} } = \displaystyle\frac{1}{ k_w } + \displaystyle\frac{ \alpha }{ k_a }$

ID:(12243, 0)

Equação

>Top, >Modelo

A relação da resistência de transferência entre o oceano e a atmosfera pode ser expressa em termos das velocidades de transferência em ambos os meios, correspondendo ao inverso da velocidade total de transferência.

Assim, utilizando la taxa total de transferência de gás no ar ($k_{ta}$), la taxa de transferência de gás na água ($k_w$), la taxa de transferência de gás no ar ($k_a$) e la solubilidade de gás ($\alpha$), estabelece-se a seguinte relação:

$\displaystyle\frac{1}{ k_{ta} } = \displaystyle\frac{1}{ k_a } + \displaystyle\frac{1}{ \alpha k_w }$

Condições

Variáveis

$\alpha$

Solubilidade de gás

$-$

9406

$k_w$

Taxa de transferência de gás na água

$m/s$

9405

$k_a$

Taxa de transferência de gás no ar

$m/s$

9407

$k_{ta}$

Taxa total de transferência de gás no ar

$m/s$

9447

Relação

Desenvolvimento

A relação envolvendo la resistência à transferência de ar para água de um gás ($R_{ta}$), determinada pela combinação de la resistência à transferência na água ($R_w$), la resistência de transferência no ar ($R_a$) e la solubilidade de gás ($\alpha$), é formulada na equação:

$R_{ta} = R_a + \displaystyle\frac{1}{ \alpha } R_w$

Isso inclui a relação de la resistência de transferência no ar ($R_a$) com la taxa de transferência de gás no ar ($k_a$) expressa em:

$R_a = \displaystyle\frac{1}{ k_a }$

Além disso, a interação de la resistência à transferência na água ($R_w$) com la taxa de transferência de gás na água ($k_w$) é explicada em:

$R_w = \displaystyle\frac{1}{ k_w }$

E a conexão entre la resistência à transferência de ar para água de um gás ($R_{ta}$) e la taxa total de transferência de gás no ar ($k_{ta}$) é especificada em:

$R_{ta} = \displaystyle\frac{1}{ k_{ta} }$

Esses elementos juntos fornecem a base para definir a relação para la taxa total de transferência de gás no ar ($k_{ta}$):

$\displaystyle\frac{1}{ k_{ta} } = \displaystyle\frac{1}{ k_a } + \displaystyle\frac{1}{ \alpha k_w }$

ID:(12242, 0)