Benützer:
Oberflächenmodell
Storyboard 
Der Austausch von Partikeln oder Molekülen, wie CO2, zwischen der Atmosphäre und dem Ozean beinhaltet einen komplexeren Mechanismus. Dieser Prozess ist mit der Bildung eines mit Partikeln oder Molekülen gesättigten Flüssigkeitsfilms verbunden, der den Transfer neuer Partikel in oder aus dem Inneren des Ozeans reguliert.
ID:(1633, 0)
Mechanismen
Iframe
Mechanismen
ID:(15640, 0)
Oberflächenschicht
Beschreibung
Um den CO2-Transfer an der Meeresoberfläche zu untersuchen, ist es notwendig, die Konzentrationsänderungen sowohl in der Luft als auch im Wasser genau zu beobachten.
In der Luft gelangt CO2 ins Wasser und erzeugt eine Zone niedriger Konzentration, in der es von $C_a$ auf $C_{a,0}$ abnimmt. Diese Schicht hat eine Dicke von 0,1 bis 1 mm.
Das in das Wasser eindringende CO2 sammelt sich zunächst an der Oberfläche an und bildet eine Konzentration $C_{w,0}$, die dann ins Innere diffundiert und eine niedrigere Konzentration von $C_w$ erreicht.
Die Konzentrationsreduktion ermöglicht die Definition von zwei Zonen: eine sehr dünne Zone von 0,02 bis 0,2 mm, in der die Konzentration schnell abnimmt, und eine zweite Zone von 0,6 bis 2 mm, in der die Konzentration allmählich abnimmt, bis sie die Konzentration im Wasser erreicht.
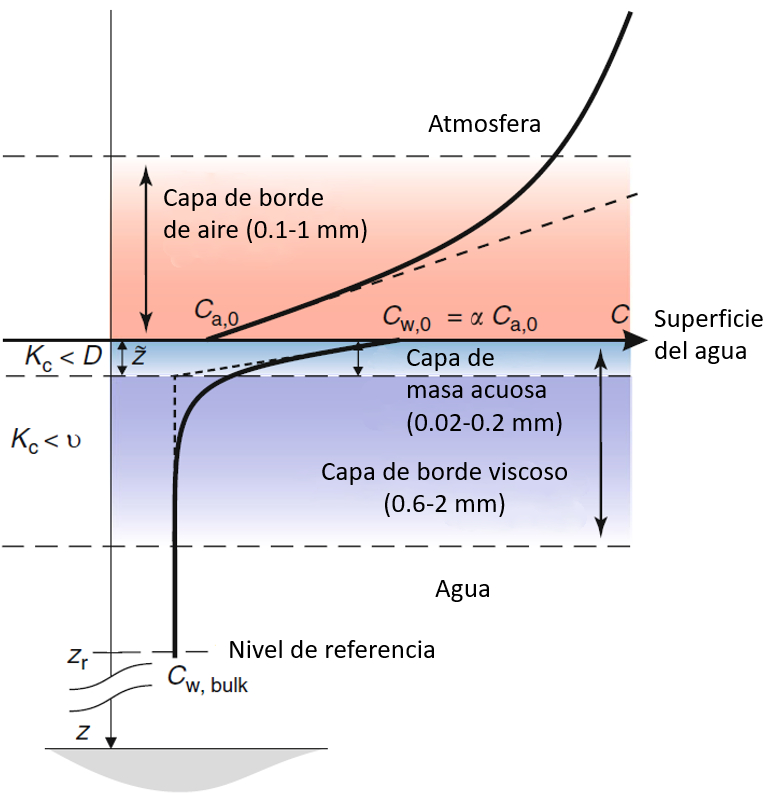
Ocean-Atmosphere Interactions of Gases and Particles, Peter S. Liss, Martin T. Johnson (eds.), Springer-Verlag Berlin Heidelberg
ID:(12244, 0)
CO2-Austausch, Geschwindigkeit aus Wasser
Konzept
Die Gasübertragungsrate in Wasser ($k_w$) kann mithilfe gemessener Daten modelliert werden. Erstens hängt es von der Geschwindigkeit ab, mit der das System Kohlenstoff von der Luft-Wasser-Grenzfläche entfernt, wodurch die Transportgeschwindigkeit proportional zur Relativgeschwindigkeit zwischen den beiden Medien wird.
Zweitens gibt es einen Effekt der Ionenmobilität, der durch der Schmidt-Nummer ($Sc$) beschrieben werden kann und die Beziehung zwischen Impulsdiffusion und Partikeln darstellt. Diese Abhängigkeit ist jedoch nicht linear und wird durch einen Faktor Exponente de Schmidt ($n$) beeinflusst, der je nach Oberflächenrauheit zwischen -1/2 und -2/3 variiert.
Schließlich hängt die Gasübertragungsrate in Wasser ($k_w$) auch von der Factor beta del transporte aire a agua de CO2 ($\beta$) ab, die wiederum durch das Rauheitsniveau der Oberfläche bestimmt wird.
Zusammenfassend wird das Gas die Gasübertragungsrate in Wasser ($k_w$) als Funktion von der Velocidad del agua ($u_w$), der Velocidad del aire ($u_a$), der Schmidt-Nummer ($Sc$), der Factor beta del transporte aire a agua de CO2 ($\beta$) und Exponente de Schmidt ($n$) wie folgt beschrieben:
| $ k_w = ( u_a - u_w ) \beta Sc ^ n $ |
ID:(15652, 0)
Löslichkeit als Funktion der Schmidt-Zahl
Konzept
Die Beweglichkeit von Molekülen, dargestellt durch die Gaslöslichkeit ($\alpha$), wird als Funktion der Partikelkonzentration modelliert, die durch der Schmidt-Nummer ($Sc$) charakterisiert ist. Diese wird wiederum aus den Parametern der Viscosidad en masa acuosa ($\eta$), der Densidad en capa de masa acuosa ($\rho$) und der Constante de difusión en masa acuosa ($D$) mithilfe des folgenden Ausdrucks berechnet:
| $ Sc =\displaystyle\frac{ \eta }{ \rho D }$ |
Diese Beziehung wird im folgenden Diagramm visualisiert:
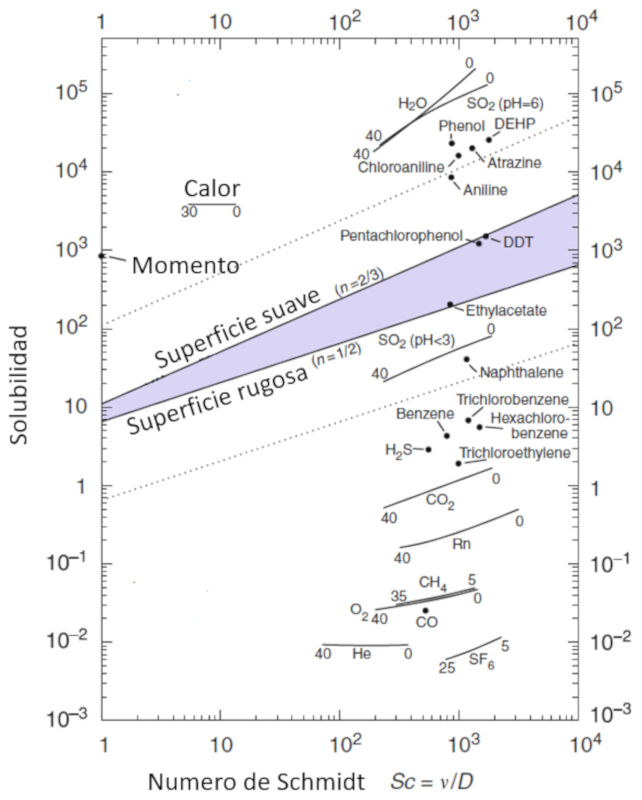
Ocean-Atmosphere Interactions of Gases and Particles, Peter S. Liss, Martin T. Johnson (eds.), Springer-Verlag Berlin Heidelberg
ID:(12245, 0)
Übertragungsgeschwindigkeit
Konzept
Die Gasübertragungsrate in Luft ($k_a$) kann aus dem Fick'schen Gesetz geschätzt werden, indem der Constante de difusión en masa acuosa ($D$) mit der Grosor de la capa superficial ($\delta_c$) wie folgt verglichen wird:
| $ k_a = \displaystyle\frac{ D }{ \delta_c }$ |
ID:(15653, 0)
Übertragungsgeschwindigkeit und Widerstände
Konzept
Für die Wechselwirkung zwischen Atmosphäre und Ozean umfasst die Luft-Wasser-Übertragungswiderstand eines Gases ($R_{ta}$) zunächst die Übergangswiderstand in Wasser ($R_w$), gefolgt vom Verdunstungsprozess $1/\alpha$ mit die Gaslöslichkeit ($\alpha$), und sobald das Gas in die Luft übergegangen ist, wirkt die Übergangswiderstand in Luft ($R_a$) darauf:
| $ R_{ta} = R_a + \displaystyle\frac{1}{ \alpha } R_w $ |
Für die Wechselwirkung zwischen Atmosphäre und Ozean umfasst die Übergangswiderstand eines Gases von Wasser zu Luft ($R_{tw}$) zunächst die Übergangswiderstand in Luft ($R_a$), gefolgt von die Gaslöslichkeit ($\alpha$), und sobald das Gas ins Wasser eingedrungen ist, kommt die Übergangswiderstand in Wasser ($R_w$) ins Spiel:
| $ R_{tw} = R_w + \alpha R_a $ |
Mit diesen Gleichungen können wir die Beziehungen für die Übertragungsgeschwindigkeiten formulieren.
Daher etablieren wir mit die Gesamtübertragungsrate von Gas in Luft ($k_{ta}$), die Gasübertragungsrate in Wasser ($k_w$), die Gasübertragungsrate in Luft ($k_a$) und die Gaslöslichkeit ($\alpha$) die folgende Beziehung:
| $ \displaystyle\frac{1}{ k_{ta} } = \displaystyle\frac{1}{ k_a } + \displaystyle\frac{1}{ \alpha k_w } $ |
Auf der anderen Seite etablieren wir mit die Gesamtübertragungsrate von Gas in Wasser ($k_{tw}$), die Gasübertragungsrate in Wasser ($k_w$), die Gasübertragungsrate in Luft ($k_a$) und die Gaslöslichkeit ($\alpha$), dass:
| $ \displaystyle\frac{1}{ k_{tw} } = \displaystyle\frac{1}{ k_w } + \displaystyle\frac{ \alpha }{ k_a } $ |
ID:(15654, 0)
Modell
Top
Parameter
Variablen
Berechnungen
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden 
Gleichungen
$ \displaystyle\frac{1}{ k_{ta} } = \displaystyle\frac{1}{ k_a } + \displaystyle\frac{1}{ \alpha k_w } $
1/ k_ta = 1/ k_a + 1/( k_w * alpha )
$ \displaystyle\frac{1}{ k_{tw} } = \displaystyle\frac{1}{ k_w } + \displaystyle\frac{ \alpha }{ k_a } $
1/ k_tw = 1/ k_w + alpha / k_a
$ C_w = \alpha C_a $
C_w = alpha * C_a
$ k_a = \displaystyle\frac{ D }{ \delta_c }$
k_a = D / delta_c
$ k_w = ( u_a - u_w ) \beta Sc ^ n $
k_w = ( u_a - u_w )* beta * Sc ^ n
$ R_a = \displaystyle\frac{1}{ k_a } $
R_a = 1/ k_a
$ R_{ta} = \displaystyle\frac{1}{ k_{ta} } $
R_ta = 1/ k_ta
$ R_{ta} = R_a + \displaystyle\frac{1}{ \alpha } R_w $
R_ta = R_a + R_w / alpha
$ R_{tw} = \displaystyle\frac{1}{ k_{tw} } $
R_tw = 1/ k_tw
$ R_{tw} = R_w + \alpha R_a $
R_tw = R_w + alpha * R_a
$ R_w = \displaystyle\frac{1}{ k_w } $
R_w = 1/ k_w
ID:(15645, 0)
Beziehungen der Oberflächenkonzentration
Gleichung
Der Konzentrationsunterschied zwischen die Gaskonzentration in der Atmosphäre ($C_a$) und die Gaskonzentration im Wasser ($C_{w,0}$) hängt von die Gaslöslichkeit ($\alpha$) ab. Daher wird die folgende Beziehung hergestellt:
| $ C_w = \alpha C_a $ |
ID:(12235, 0)
Übertragungsgeschwindigkeit
Gleichung
Die Gasübertragungsrate in Luft ($k_a$) kann aus dem Fick'schen Gesetz geschätzt werden, indem der Constante de difusión en masa acuosa ($D$) mit der Grosor de la capa superficial ($\delta_c$) wie folgt verglichen wird:
| $ k_a = \displaystyle\frac{ D }{ \delta_c }$ |
ID:(12227, 0)
CO2-Austausch, Geschwindigkeit aus Wasser
Gleichung
Der Gasparameter die Gasübertragungsrate in Wasser ($k_w$) wird in Bezug auf der Velocidad del agua ($u_w$), der Velocidad del aire ($u_a$), der Schmidt-Nummer ($Sc$), der Factor beta del transporte aire a agua de CO2 ($\beta$) und Exponente de Schmidt ($n$) wie folgt beschrieben:
| $ k_w = ( u_a - u_w ) \beta Sc ^ n $ |
ID:(12215, 0)
Übertragungsrate und Widerstand in der Atmosphäre
Gleichung
Die Übergangswiderstand in Luft ($R_a$) wird als das Inverse von die Gasübertragungsrate in Luft ($k_a$) definiert. Diese Beziehung kann wie folgt ausgedrückt werden:
| $ R_a = \displaystyle\frac{1}{ k_a } $ |
ID:(12236, 0)
Übertragungsrate und Widerstand im Ozean
Gleichung
Die Übergangswiderstand in Wasser ($R_w$) wird als das Inverse von die Gasübertragungsrate in Wasser ($k_w$) definiert. Diese Beziehung kann wie folgt ausgedrückt werden:
| $ R_w = \displaystyle\frac{1}{ k_w } $ |
ID:(12237, 0)
Gesamtübertragungsrate Atmosphäre-Ozean
Gleichung
Die Übergangswiderstand eines Gases von Wasser zu Luft ($R_{tw}$) wird als das Inverse von die Gesamtübertragungsrate von Gas in Wasser ($k_{tw}$) definiert. Diese Beziehung kann wie folgt ausgedrückt werden:
| $ R_{tw} = \displaystyle\frac{1}{ k_{tw} } $ |
ID:(12238, 0)
Gesamtübertragungsrate Ozean-Atmosphäre
Gleichung
Die Luft-Wasser-Übertragungswiderstand eines Gases ($R_{ta}$) wird als das Inverse von die Gesamtübertragungsrate von Gas in Luft ($k_{ta}$) definiert. Diese Beziehung kann wie folgt ausgedrückt werden:
| $ R_{ta} = \displaystyle\frac{1}{ k_{ta} } $ |
ID:(12239, 0)
Völliger Widerstand gegen die Übertragung von Ozean und Atmosphäre
Gleichung
Für die Wechselwirkung zwischen der Atmosphäre und dem Ozean umfasst die Luft-Wasser-Übertragungswiderstand eines Gases ($R_{ta}$) zunächst die Übergangswiderstand in Wasser ($R_w$), gefolgt vom Verdunstungsprozess $1/\alpha$ mit die Gaslöslichkeit ($\alpha$). Sobald das Gas in die Luft übergegangen ist, wirkt die Übergangswiderstand in Luft ($R_a$) darauf:
| $ R_{ta} = R_a + \displaystyle\frac{1}{ \alpha } R_w $ |
ID:(12240, 0)
Völliger Widerstand gegen den Atmosphäre-Ozean-Transfer
Gleichung
Für die Wechselwirkung zwischen der Atmosphäre und dem Ozean umfasst die Übergangswiderstand eines Gases von Wasser zu Luft ($R_{tw}$) zunächst die Übergangswiderstand in Luft ($R_a$), gefolgt von die Gaslöslichkeit ($\alpha$). Sobald das Gas ins Wasser eingedrungen ist, wirkt die Übergangswiderstand in Wasser ($R_w$):
| $ R_{tw} = R_w + \alpha R_a $ |
ID:(12241, 0)
Atmosphäre-Ozean-Transferrate
Gleichung
Das Verhältnis zwischen dem Transferwiderstand zwischen der Atmosphäre und dem Ozean kann in Bezug auf die Transfergeschwindigkeiten in beiden Medien ausgedrückt werden, was dem Kehrwert der gesamten Transfergeschwindigkeit entspricht.
Daher wird mit die Gesamtübertragungsrate von Gas in Wasser ($k_{tw}$), die Gasübertragungsrate in Wasser ($k_w$), die Gasübertragungsrate in Luft ($k_a$) und die Gaslöslichkeit ($\alpha$) festgestellt, dass:
| $ \displaystyle\frac{1}{ k_{tw} } = \displaystyle\frac{1}{ k_w } + \displaystyle\frac{ \alpha }{ k_a } $ |
Die Beziehung zwischen die Übergangswiderstand eines Gases von Wasser zu Luft ($R_{tw}$), die durch die Summen von die Übergangswiderstand in Wasser ($R_w$), die Übergangswiderstand in Luft ($R_a$) und die Gaslöslichkeit ($\alpha$) hergestellt wird, wird in der Gleichung ausgedrückt:
| $ R_{tw} = R_w + \alpha R_a $ |
Einschließlich der Beziehung von die Übergangswiderstand in Luft ($R_a$) mit die Gasübertragungsrate in Luft ($k_a$) in:
| $ R_a = \displaystyle\frac{1}{ k_a } $ |
Die Interaktion von die Übergangswiderstand in Wasser ($R_w$) mit die Gasübertragungsrate in Wasser ($k_w$) wird beschrieben in:
| $ R_w = \displaystyle\frac{1}{ k_w } $ |
Und die Verbindung zwischen die Übergangswiderstand eines Gases von Wasser zu Luft ($R_{tw}$) und die Gesamtübertragungsrate von Gas in Wasser ($k_{tw}$) wird detailliert in:
| $ R_{tw} = \displaystyle\frac{1}{ k_{tw} } $ |
Dies bildet die Grundlage für die Festlegung der Beziehung für die Gesamtübertragungsrate von Gas in Wasser ($k_{tw}$):
| $ \displaystyle\frac{1}{ k_{tw} } = \displaystyle\frac{1}{ k_w } + \displaystyle\frac{ \alpha }{ k_a } $ |
ID:(12243, 0)
Übertragungsrate Ozean-Atmosphäre
Gleichung
Das Verhältnis des Transferwiderstands zwischen dem Ozean und der Atmosphäre kann in Bezug auf die Transfergeschwindigkeiten in beiden Medien ausgedrückt werden, was dem Kehrwert der gesamten Transfergeschwindigkeit entspricht.
Daher wird unter Verwendung von die Gesamtübertragungsrate von Gas in Luft ($k_{ta}$), die Gasübertragungsrate in Wasser ($k_w$), die Gasübertragungsrate in Luft ($k_a$) und die Gaslöslichkeit ($\alpha$) die folgende Beziehung festgelegt:
| $ \displaystyle\frac{1}{ k_{ta} } = \displaystyle\frac{1}{ k_a } + \displaystyle\frac{1}{ \alpha k_w } $ |
Die Beziehung, die die Luft-Wasser-Übertragungswiderstand eines Gases ($R_{ta}$) involviert und durch die Kombination von die Übergangswiderstand in Wasser ($R_w$), die Übergangswiderstand in Luft ($R_a$) und die Gaslöslichkeit ($\alpha$) bestimmt wird, ist in der Gleichung formuliert:
| $ R_{ta} = R_a + \displaystyle\frac{1}{ \alpha } R_w $ |
Dies schließt die Beziehung von die Übergangswiderstand in Luft ($R_a$) mit die Gasübertragungsrate in Luft ($k_a$) ein, die ausgedrückt wird in:
| $ R_a = \displaystyle\frac{1}{ k_a } $ |
Zusätzlich wird die Interaktion von die Übergangswiderstand in Wasser ($R_w$) mit die Gasübertragungsrate in Wasser ($k_w$) erklärt in:
| $ R_w = \displaystyle\frac{1}{ k_w } $ |
Und die Verbindung zwischen die Luft-Wasser-Übertragungswiderstand eines Gases ($R_{ta}$) und die Gesamtübertragungsrate von Gas in Luft ($k_{ta}$) wird spezifiziert in:
| $ R_{ta} = \displaystyle\frac{1}{ k_{ta} } $ |
Diese Elemente zusammen liefern die Grundlage zur Definition der Beziehung für die Gesamtübertragungsrate von Gas in Luft ($k_{ta}$):
| $ \displaystyle\frac{1}{ k_{ta} } = \displaystyle\frac{1}{ k_a } + \displaystyle\frac{1}{ \alpha k_w } $ |
ID:(12242, 0)