Moment exchange
Storyboard 
The exchange of momentum between the atmosphere and the ocean refers to the process by which the atmosphere drives the ocean, generating corresponding ocean currents.
Ocean-Atmosphere Interactions of Gases and Particles, Peter S. Liss, Martin T. Johnson (eds.). Springer, 2014
Chapter: Transfer Across the Air-Sea Interface
ID:(1631, 0)
Surface tension
Description 
The wind over the ocean surface is composed of a large number of molecules that periodically collide with water molecules at the surface.
In this way, the kinetic energy of the air molecules is partially transferred to the water molecules, which can be represented as a stress exerted by the air onto the water.
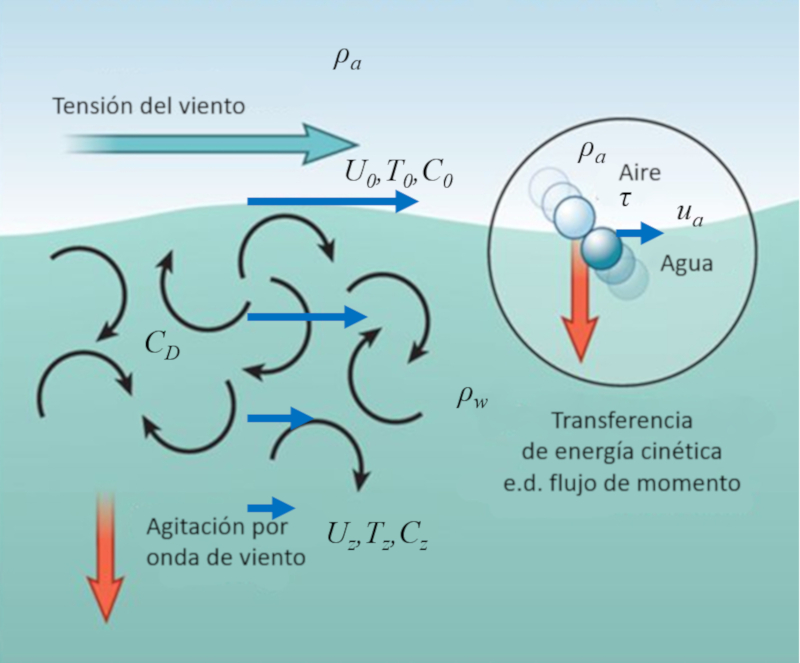
The resulting effect is the creation of surface eddies, which in turn affect deeper layers, transferring the velocity of the wind to a shallow layer of the ocean. This process allows the energy of the wind to be transferred to the near-surface layer of the ocean, increasing the speed of the water in that area.
ID:(12303, 0)
General scheme of types of disturbances
Image 
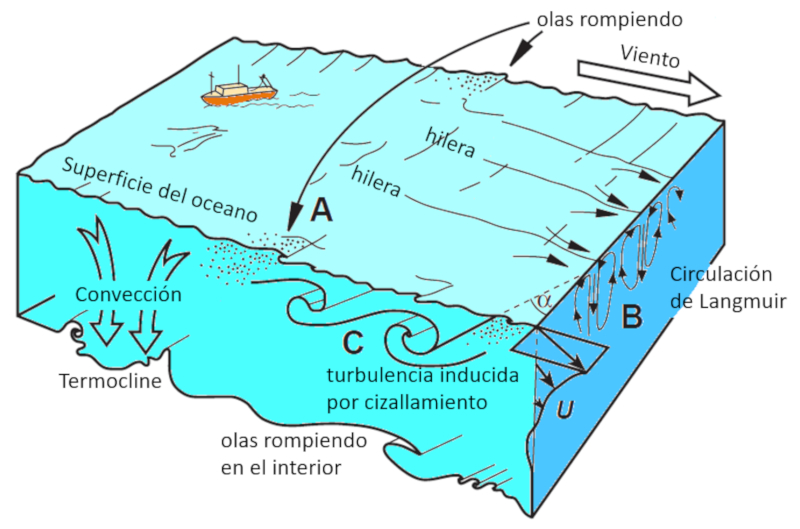
Generally, when observing the ocean, various mechanisms generating vortices and turbulence are evident, contributing to mixing processes.
Within the surface layer, notable features include:
• Surface waves generated by winds.
• Langmuir circulation, forming visible streaks from the air.
• Breaking of surface waves.
Meanwhile, between the lower boundary of the mixing layer and the thermocline, prominent factors include:
• Turbulence due to shear at the upper boundary.
• Internal waves breaking at the lower boundary.
• Convection.
• Vertical instabilities.
These phenomena are depicted in the following diagram:
ID:(12180, 0)
Langmuir stable waves
Description 
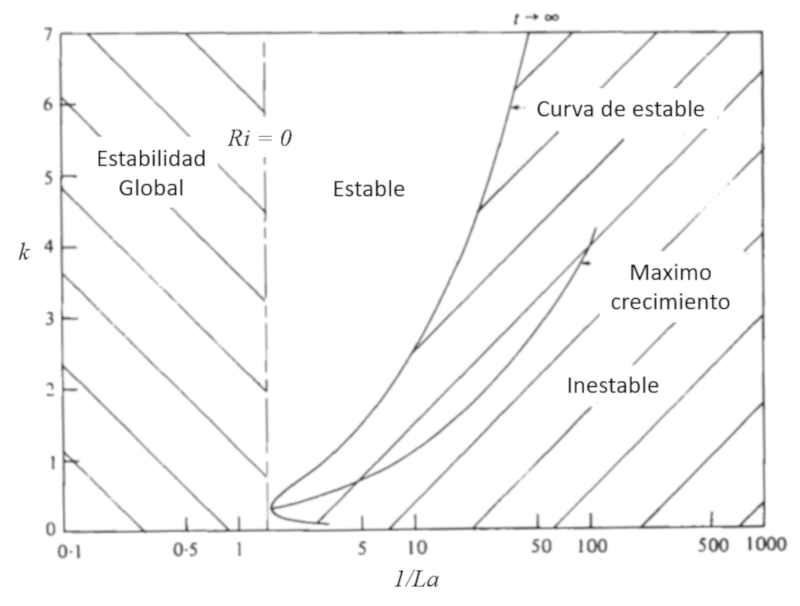
One of the phenomena originating from wind-induced surface currents is called the Langmuir circulation:

The instability of the ocean to Langmuir circulations, S. Leibovich and S. Paoluccit, J. Fluid Mech. (1981). vol. 102, pp. 141-167
It originates similarly to Ekman transport, where due to the Coriolis force, there are areas of downwelling that generate upwelling eddies. The circulation closes with the formation of an upwelling zone:

In the article cited in the next image, it is concluded that there are specific conditions for the formation of Langmuir circulation, which depend on various conditions and the oscillation itself:
ID:(12221, 0)
Model
Top 
Parameters
Variables
Calculations
Calculations
Calculations
Equations
$ k_w = ( u_a - u_w ) \beta Sc ^ n $
k_w = ( u_a - u_w )* beta * Sc ^ n
$ La = \sqrt{\displaystyle\frac{ u_a }{ u_w }}$
La = sqrt( u_a / u_w )
$ \tau = \tau_t + \tau_w + \tau_{\eta} $
tau = tau_t + tau_w + tau_eta
$ \tau_t = \rho_a C_D ( u_a - u_w )^2$
tau_t = rho_a * C_D * ( u_a - u_w )^2
$ \tau_t = \rho_a u_a ^2 $
tau_t = rho_a * u_a ^2
$ \displaystyle\frac{ u_a ^2 }{ u_w ^2 } = \displaystyle\frac{ \rho_w }{ \rho_a }$
u_a ^2/ u_w ^2 = rho_w / rho_a
ID:(15643, 0)
Velocity profile in the superficial layer (MOST)
Equation 
The force the tensión del viento ($\tau_t$) exerted on the surface can be modeled according to the Monin-Obukhov Similarity Theory (MOST) as the transfer of kinetic energy from the air to the upper layer of the ocean.
For this, it is assumed that the tensión del viento ($\tau_t$) is proportional to the densidad del aire ($\rho_a$) and to the square difference between the velocidad del aire ($u_a$) and the velocidad del agua ($u_w$). The proportionality is considered by introducing the constante de arrastre ($C_D$), leading to the conclusion that:
ID:(12222, 0)
Surface tension (MOST)
Equation 
The Monin-Obukhov Similarity Theory (MOST) model depicts the surface tension proportional to the square of the velocidad del aire ($u_a$) at the surface and to the densidad del aire ($\rho_a$).
In this case, the surface fraction is estimated through the kinetic energy density, which correlates with the surface tension.
Therefore, it is estimated that the velocidad del aire ($u_a$) is
None
ID:(12220, 0)
Total voltage at the interface
Equation 
The variable the tensión superficial aire-agua ($\tau$) includes the tensión del viento ($\tau_t$), the tensión de las olas ($\tau_w$), and the tensión de la viscosidad ($\tau_{\eta}$). Therefore, it can be expressed as:
ID:(12232, 0)
Speed ratio
Equation 
If we assume a continuous transition in energy density at the interface between air and water, and consider this energy to be kinetic in nature, then with the densidad del aire ($\rho_a$), the velocidad del aire ($u_a$), and the densidad del agua ($\rho_w$), the velocidad del agua ($u_w$), we can establish the following relationship:
$\rho_a u_a^2=\rho_w u_w^2$
Therefore, we can establish the relationship:
Additionally, we can consider that the energy density has the same unit as surface tension, which explains the equality, as in an equilibrium system, tensions must be equal.
ID:(12234, 0)
Langmuir Number
Equation 
The relationship between the velocidad del aire ($u_a$) and the velocidad del agua ($u_w$) is studied through the numero de Langmuir ($La$). Therefore, the Langmuir number can be defined as the ratio of the square root of both velocities:
ID:(12219, 0)
CO2 exchange, speed from water
Equation 
The gas parameter the gas transfer rate in water ($k_w$) is described in terms of the velocidad del agua ($u_w$), the velocidad del aire ($u_a$), the schmidt number ($Sc$), the factor beta del transporte aire a agua de CO2 ($\beta$), and exponente de Schmidt ($n$) as follows:
ID:(12215, 0)
