User:
Heat exchange
Storyboard 
The exchange of heat between the atmosphere and the ocean refers to the process by which the atmosphere transfers or absorbs heat from the ocean, thereby equalizing the temperatures between the two.
Ocean-Atmosphere Interactions of Gases and Particles, Peter S. Liss, Martin T. Johnson (eds.). Springer, 2014
Chapter: Transfer Across the Air-Sea Interface
ID:(1580, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ \delta_c = \sqrt{\displaystyle\frac{ \rho D }{ \eta }} \delta_{\eta}$
delta_c =sqrt( D * rho / eta )* delta_eta
$ \epsilon = \displaystyle\frac{ \eta ^3 }{ \rho ^3 \delta_{\eta} ^4 }$
epsilon = eta ^3/( rho ^3* delta_eta ^4 )
$ H_z = C_H \rho_a c_p ( T_z - T_0 ) U_z $
H_z = C_H *rho_a * c_p * ( T_z - T_0 )* U_z
ID:(15642, 0)
Surface layer temperature profile (MOST)
Equation
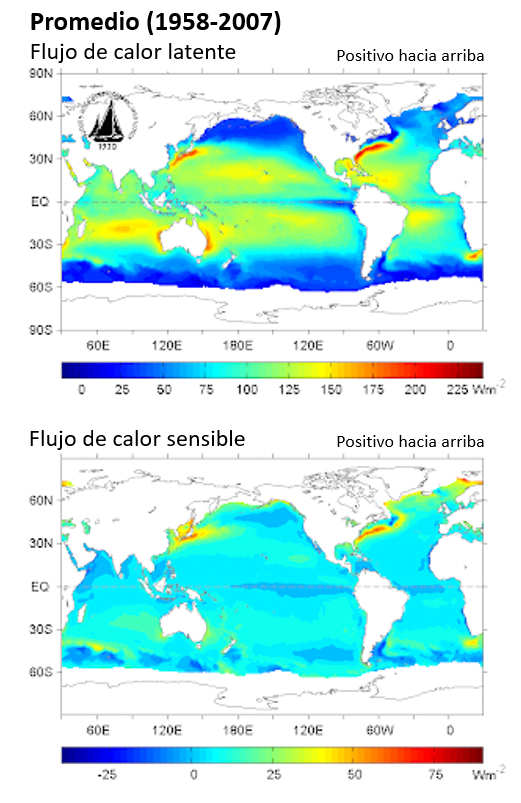
In the case of heat flux, the heat content is estimated using density, specific heat, and temperature, along with the wind velocity and the transmission coefficient. In this way, the heat flux can be expressed as follows:
| $ H_z = C_H \rho_a c_p ( T_z - T_0 ) U_z $ |
In the Monin-Obukhov Similarity Theory (MOST), the surface heat energy, represented by
$\rho_a c_p (T_z - T_0)$
is transferred to the water with the transfer coefficient $C_H$ and the air velocity $U_z$, resulting in the heat flux.
| $ H_z = C_H \rho_a c_p ( T_z - T_0 ) U_z $ |
ID:(12223, 0)
Energy dissipation in surface layer
Equation
La energía disipada se puede estimar de la viscosidad, densidad y grosor de la capa.
Por ello con es
| $ \epsilon = \displaystyle\frac{ \eta ^3 }{ \rho ^3 \delta_{\eta} ^4 }$ |
ID:(12230, 0)
Surface thickness and viscous layer
Equation
El grosor de la superficie y de la capa viscosas son proposicionales siendo la constante una función de la constante difusión, viscosidad y densidad.
Por ello con es
| $ \delta_c = \sqrt{\displaystyle\frac{ \rho D }{ \eta }} \delta_{\eta}$ |
ID:(12229, 0)