Storyboard

A troca de substâncias entre a atmosfera e o oceano pode incluir partículas. Isso é particularmente relevante ao estudar a transferência de moléculas de CO2 da atmosfera para o oceano.

Ocean-Atmosphere Interactions of Gases and Particles, Peter S. Liss, Martin T. Johnson (eds.). Springer, 2014

Chapter: Transfer Across the Air-Sea Interface

>Modelo

ID:(1630, 0)

Iframe

>Top

ID:(15636, 0)

Descrição

>Top

O CO2 é absorvido pelos oceanos, contribuindo para mitigar o efeito desse gás na atmosfera e, assim, retardar as mudanças climáticas. No entanto, os processos envolvidos são mais complexos e incluem:

- Trocas gasosas com a atmosfera: O oceano e a atmosfera estão constantemente em intercâmbio de CO2 por meio da difusão de gases. O CO2 atmosférico se dissolve na superfície do oceano e forma ácido carbônico (H2CO3), que por sua vez se dissocia em íons hidrogênio (H+) e bicarbonato (HCO3-). Esse processo ajuda a equilibrar os níveis de CO2 entre o oceano e a atmosfera.

- Fotossíntese e respiração: Organismos marinhos, como o fitoplâncton e as algas, realizam a fotossíntese e absorvem CO2 da água para produzir matéria orgânica e liberar oxigênio. Esse processo, conhecido como fixação de carbono, auxilia na remoção de CO2 do oceano. Por outro lado, os organismos marinhos também respiram, liberando CO2 na água durante o processo de decomposição da matéria orgânica.

- Circulação oceânica: O oceano possui uma circulação global, na qual as correntes transportam água rica em CO2 da superfície para as profundezas e vice-versa. Isso contribui para a distribuição e mistura do CO2 em todo o oceano, permitindo que as águas profundas armazenem grandes quantidades de CO2 dissolvido.

- Sedimentação e soterramento: Parte da matéria orgânica produzida por organismos marinhos, incluindo o CO2 capturado por meio da fotossíntese, pode afundar e ser depositada no fundo do oceano. Conforme os sedimentos se acumulam ao longo do tempo geológico, o carbono orgânico é soterrado e pode ser armazenado no leito marinho por longos períodos de tempo.

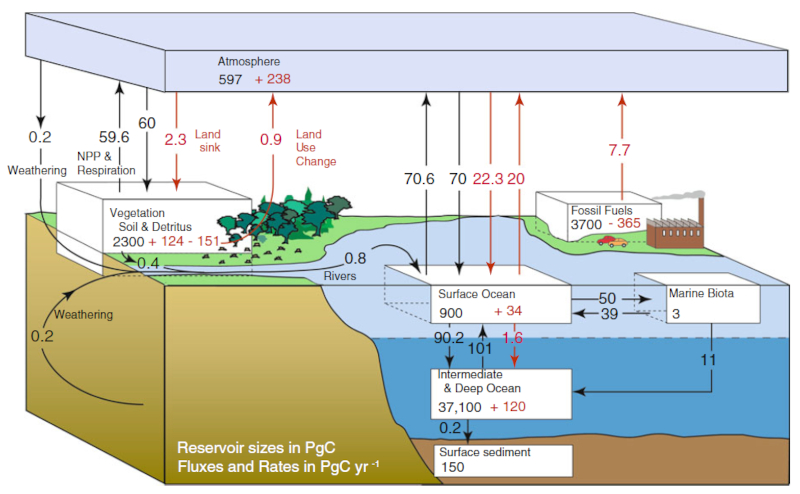
Fluxo anual de carbono em PgC/ano. Os números em preto são a pré-revolução industrial, em vermelho são os aumentos relacionados à revolução industrial. Ocean-Atmosphere Interactions of Gases and Particles, Peter S. Liss Martin T. Johnson (Editors), Springer, 2014

Dependendo da área e da época do planeta, há maior concentração de carbono na atmosfera do que no oceano ou vice-versa, definindo assim se o fluxo de carbono é do ar para a água ou vice-versa.

ID:(12297, 0)

Descrição

>Top

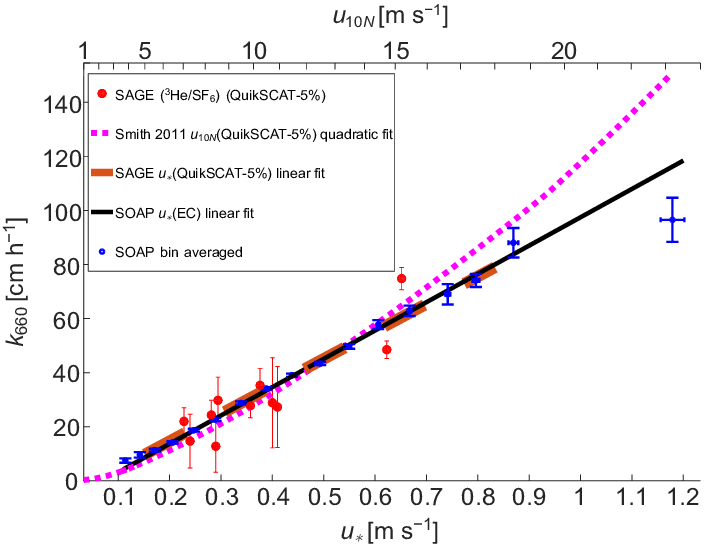
Em uma primeira aproximação, a dependência de la taxa de transferência de gás na água ($k_w$) em relação à velocidade relativa, calculada subtraindo ($$) de ($$), é proporcional a

$k_w \propto u_a - u_w$

como observado no gráfico:

ID:(12298, 0)

Descrição

>Top

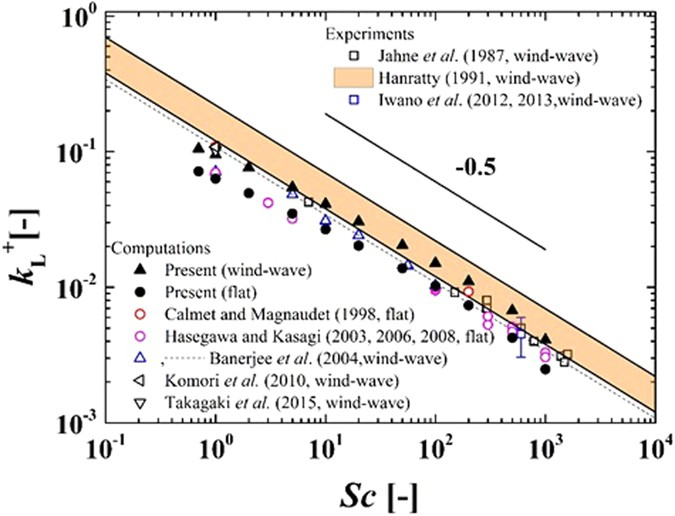
A relação entre la taxa de transferência de gás na água ($k_w$) é inversamente proporcional a o número Schmidt ($Sc$), portanto, é expressa como proporcional a esse número elevado a ($$), que é negativo:

$k_w\propto Sc^n$

isso é representado com ($$) igual a -0.5:

ID:(12299, 0)

Conceito

>Top

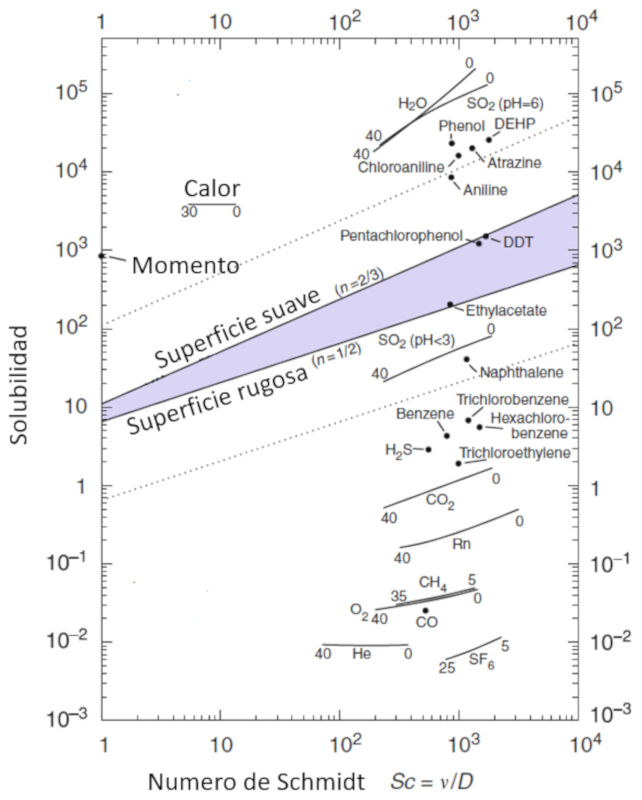
A mobilidade das moléculas, representada por la solubilidade de gás ($\alpha$), é uma função da concentração de partículas, descrita por o número Schmidt ($Sc$), que por sua vez é calculada a partir de ($$), ($$) e ($$) utilizando a seguinte equação:

Essa relação é ilustrada no seguinte diagrama:

ID:(12245, 0)

Conceito

>Top

La taxa de transferência de gás na água ($k_w$) pode ser modelada usando dados medidos. Em primeiro lugar, depende da velocidade com que o sistema remove carbono da interface ar-água, tornando a velocidade de transporte proporcional à velocidade relativa entre os dois meios.

Em segundo lugar, há um efeito da mobilidade dos íons, que pode ser descrito por o número Schmidt ($Sc$), representando a relação entre a difusão de momento e as partículas. No entanto, essa dependência não é linear e é influenciada por um fator ($$) que varia entre -1/2 e -2/3 dependendo da rugosidade da superfície.

Finalmente, la taxa de transferência de gás na água ($k_w$) também depende de ($$), que por sua vez é determinada pelo nível de rugosidade da superfície.

Em resumo, o gás la taxa de transferência de gás na água ($k_w$) é descrito em função de ($$), ($$), o número Schmidt ($Sc$), ($$) e ($$) da seguinte maneira:

ID:(15652, 0)

Top

>Top

Parâmetros

$D_C$

D_C

Constante de transmissão de concentração

-

$F_a$

F_a

Densidade de fluxo de gás atmosfera-oceano

1/m^2s

$\Delta p_{gas}$

Dp_gas

Diferença de pressão parcial de gás entre água e ar

Pa

$C$

C

Fluxo de concentração

$Sc$

Sc

Número Schmidt

-

$\alpha$

alpha

Solubilidade de gás

-

$k_a$

k_a

Taxa de transferência de gás no ar

m/s

Variáveis

$C_{w,0}$

C_w0

Concentração de gás na água

1/m^3

$C_a$

C_a

Concentração de gás na atmosfera

1/m^3

$k_w$

k_w

Taxa de transferência de gás na água

m/s

Cálculos

• Método alternativo
• Método tradicional
• Estratégia
• 2D
• 3D

Equação

Equação

Primeiro, selecione a equação: para , depois, selecione a variável: para

---

Cálculos

Símbolo

Equação

Resolvido

Traduzido

Cálculos

Símbolo

Equação

Resolvido

Traduzido

Variáve Dado Calcular Objetivo : Equação A ser usado

Equações

ID:(15641, 0)

Equação

>Top, >Modelo

Uma vez que o fluxo difusivo $F$ pode ser modelado usando a lei de Fick:

Podemos estabelecer uma relação entre a velocidade de transferência $k$ e a diferença de concentração $\Delta C$ da seguinte forma:

$F_a =- k_a \Delta p_{gas}$

Condições

Variáveis

$F_a$

Densidade de fluxo de gás atmosfera-oceano

$1/m^2s$

9400

$\Delta p_{gas}$

Diferença de pressão parcial de gás entre água e ar

$Pa$

9404

$k_a$

Taxa de transferência de gás no ar

$m/s$

9407

Relação

Desenvolvimento

O fluxo difusivo $F$ é descrito pela lei de Fick:

$F = - D \displaystyle\frac{d C }{d t }$

onde $D$ é a constante de difusão e $dC/dx$ é o gradiente de concentração. Ao definirmos uma velocidade de transferência da seguinte maneira:

$k_a = \displaystyle\frac{ D }{ \delta_c }$

podemos estabelecer uma equação de fluxo do tipo:

$F_a =- k_a \Delta p_{gas}$

ID:(12226, 0)

Equação

>Top, >Modelo

Utilizando o modelo de similaridade de Monin-Obukhov (MOST), é possível estimar o fluxo de elementos, como gases, levando em consideração o deslocamento da superfície e um coeficiente de transferência, expresso da seguinte forma:

$C = D_C U_z ( C_z - C_0 )$

Condições

Variáveis

$D_C$

Constante de transmissão de concentração

$-$

10066

$C$

Fluxo de concentração

$kg/m^2s$

10067

Relação

Desenvolvimento

No modelo de similaridade de Monin-Obukhov (MOST), o fluxo de elementos como gases é estimado considerando a diferença de concentrações entre o ar e a água, representada por

$C_z - C_0$

e o fluxo é calculado utilizando o coeficiente de transferência $D_C$ e a velocidade da superfície $U_z$, da seguinte forma:

$C = D_C U_z ( C_z - C_0 )$

Isso permite estimar o fluxo dos elementos entre o ar e a água.

ID:(12224, 0)

Equação

>Top, >Modelo

O gradiente de concentração entre la concentração de gás na atmosfera ($C_a$) e la concentração de gás na água ($C_{w,0}$) depende de la solubilidade de gás ($\alpha$). Portanto, estabelece-se a seguinte relação:

$C_w = \alpha C_a$

Condições

Variáveis

$C_w$

Concentração de gás na água

$1/m^3$

9415

$C_a$

Concentração de gás na atmosfera

$1/m^3$

9416

$\alpha$

Solubilidade de gás

$-$

9406

Relação

ID:(12235, 0)

Equação

>Top, >Modelo

A velocidade de transferência de uma quantidade $k$ é definida como o fluxo $F$ dividido pela diferença de concentração entre os dois meios, representada por

$C_0-C_b$

Portanto, pode ser expressa como:

$k =\displaystyle\frac{ F }{ C_0 - C_b }$

Condições

Variáveis

$F$

Densidade de fluxo de gás atmosfera-oceano

$1/m^2s$

9400

Relação

ID:(12213, 0)

Equação

>Top, >Modelo

La taxa de transferência de gás no ar ($k_a$) pode ser estimado a partir da lei de Fick, comparando ($$) com ($$) da seguinte maneira:

$k_a = \displaystyle\frac{ D }{ \delta_c }$

Condições

Variáveis

$k_a$

Taxa de transferência de gás no ar

$m/s$

9407

Relação

ID:(12227, 0)

Equação

>Top, >Modelo

A velocidade de transferência de CO2 da atmosfera para a água pode ser modelada usando uma equação similar à regra geral

Nesse modelo, a diferença de concentração é substituída pela diferença de pressão parcial do gás e sua solubilidade $\alpha$. A equação pode ser expressa da seguinte forma:

$F_w = k_w \Delta p_{gas}$

Condições

Variáveis

$\Delta p_{gas}$

Diferença de pressão parcial de gás entre água e ar

$Pa$

9404

$k_w$

Taxa de transferência de gás na água

$m/s$

9405

Relação

Desenvolvimento

Se considerarmos o fluxo de gás como $F$ e a velocidade de transporte como $k$, de acordo com a relação geral:

$k =\displaystyle\frac{ F }{ C_0 - C_b }$

Ao substituirmos a diferença de concentração $C_0 - C_b$ pela diferença na pressão parcial do gás usando a solubilidade $\alpha$, temos:

$C_0 - C_b = \alpha \Delta p_{CO2}$

obtemos:

$F_w = k_w \Delta p_{gas}$

ID:(12214, 0)

Equação

>Top, >Modelo

O parâmetro do gás la taxa de transferência de gás na água ($k_w$) é descrito em termos de ($$), ($$), o número Schmidt ($Sc$), ($$) e ($$) da seguinte forma:

$k_w = ( u_a - u_w ) \beta Sc ^ n$

Condições

Variáveis

$Sc$

Número Schmidt

$-$

9410

$k_w$

Taxa de transferência de gás na água

$m/s$

9405

Relação

ID:(12215, 0)

Equação

>Top, >Modelo

O número de Schmidt estabelece uma relação entre a difusão viscosa

e a difusão de partículas

.

A difusão viscosa é igual à viscosidade dividida pela densidade, enquanto a difusão de partículas corresponde à constante de difusão. Portanto, ele é definido da seguinte forma:

$Sc =\displaystyle\frac{ \eta }{ \rho D }$

Condições

Variáveis

$Sc$

Número Schmidt

$-$

9410

Relação

ID:(12216, 0)

Equação

>Top, >Modelo

ID:(12229, 0)