Storyboard

El intercambio de sustancias entre la atmósfera y el océano puede incluir partículas. Esto es particularmente relevante al estudiar la transferencia de moléculas de CO2 desde la atmósfera hacia el océano.

Ocean-Atmosphere Interactions of Gases and Particles, Peter S. Liss, Martin T. Johnson (eds.). Springer, 2014

Chapter: Transfer Across the Air-Sea Interface

>Modelo

ID:(1630, 0)

Iframe

>Top

ID:(15636, 0)

Descripción

>Top

El CO2 es absorbido por los océanos contribuyendo a frenar el efecto de este gas en la atmósfera y retrasando por ello el cambio climático. Sin embargo los procesos son más complejos e incluyen:

- Intercambio gaseoso con la atmósfera: El océano y la atmósfera están en constante intercambio de CO2 a través de la difusión de gases. El CO2 atmosférico se disuelve en la superficie del océano y forma ácido carbónico (H2CO3), que a su vez se disocia en iones hidrógeno (H+) y bicarbonato (HCO3-). Este proceso ayuda a equilibrar los niveles de CO2 entre el océano y la atmósfera.

- Fotosíntesis y respiración: Los organismos marinos, como el fitoplancton y las algas, realizan la fotosíntesis y toman CO2 del agua para producir materia orgánica y liberar oxígeno. Este proceso, conocido como fijación de carbono, ayuda a extraer CO2 del océano. Por otro lado, los organismos marinos también respiran, lo que significa que liberan CO2 al agua durante el proceso de descomposición de la materia orgánica.

- Circulación oceánica: El océano se caracteriza por su circulación global, en la cual las corrientes transportan agua rica en CO2 desde la superficie hacia las profundidades y viceversa. Esto contribuye a la distribución y mezcla del CO2 en todo el océano, permitiendo que las aguas profundas almacenen grandes cantidades de CO2 disuelto.

- Sedimentación y enterramiento: Parte de la materia orgánica producida por los organismos marinos, incluido el CO2 capturado a través de la fotosíntesis, puede hundirse hacia el fondo del océano. A medida que los sedimentos se acumulan a lo largo del tiempo geológico, el carbono orgánico se entierra y puede quedar almacenado en el fondo marino durante períodos muy largos.

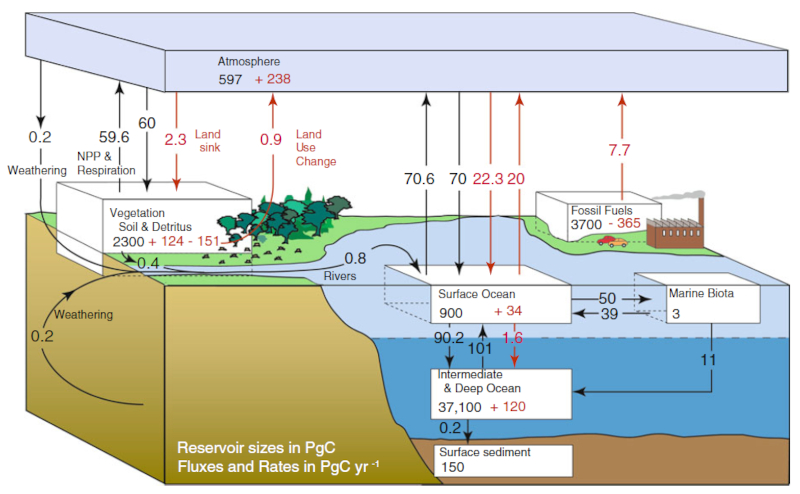
Flujo de carbono anual en PgC/yr. Numeros en negro son pre revolución industrial, en rojo incrementos relacionados con la revolución industrial. Ocean-Atmosphere Interactions of Gases and Particles, Peter S. Liss Martin T. Johnson (Editors), Springer, 2014

Según la zona y epoca del planeta existe una concnetración de carbolno mayor en la atmosfera que en el oceano o vice versa y con ello definiendo si el flujo de carbono es del aire al agua o viceversa.

Según la zona y epoca del planeta existe una concnetración de carbolno mayor en la atmosfera que en el oceano o vice versa y con ello definiendo si el flujo de carbono es del aire al agua o viceversa.

ID:(12297, 0)

Descripción

>Top

En una primera aproximación, la dependencia de la velocidad de transferencia del gas en el agua ($k_w$) con respecto a la velocidad relativa, calculada restando el velocidad del agua ($u_w$) de el velocidad del aire ($u_a$), es proporcional a

$k_w \propto u_a - u_w$

como se observa en el gráfico:

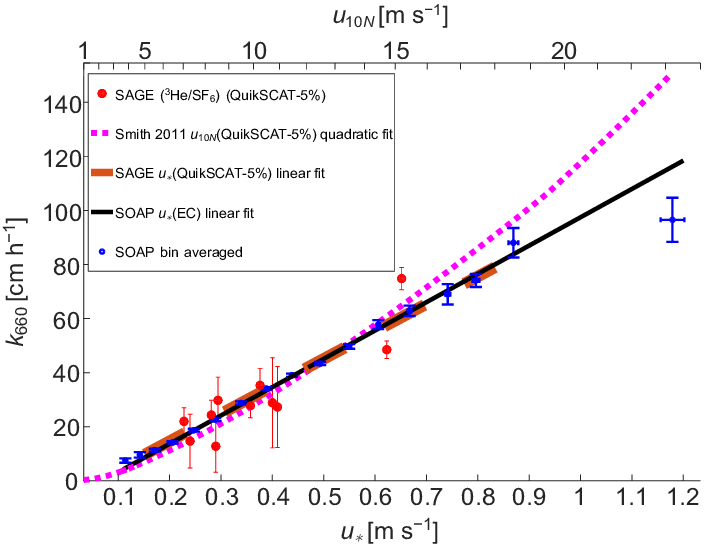
ID:(12298, 0)

Descripción

>Top

La relación entre la velocidad de transferencia del gas en el agua ($k_w$) es inversamente proporcional a el número de Schmidt ($Sc$), por lo que se expresa proporcional a dicho número elevado a exponente de Schmidt ($n$), que es negativo:

$k_w\propto Sc^n$

ce qui est représenté avec exponente de Schmidt ($n$) égal à -0.5 :

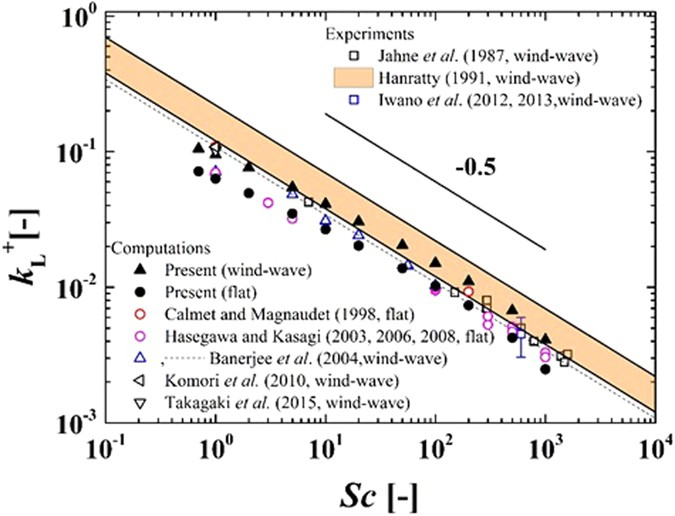
ID:(12299, 0)

Concepto

>Top

La movilidad de las moléculas, representada por la solubilidad del gas ($\alpha$), se modela como una función de la concentración de las partículas, caracterizada por el número de Schmidt ($Sc$), que a su vez se calcula a partir de los parámetros el viscosidad en masa acuosa ($\eta$), el densidad en capa de masa acuosa ($\rho$), y el constante de difusión en masa acuosa ($D$) utilizando la siguiente expresión:

Esta relación se visualiza en el siguiente diagrama:

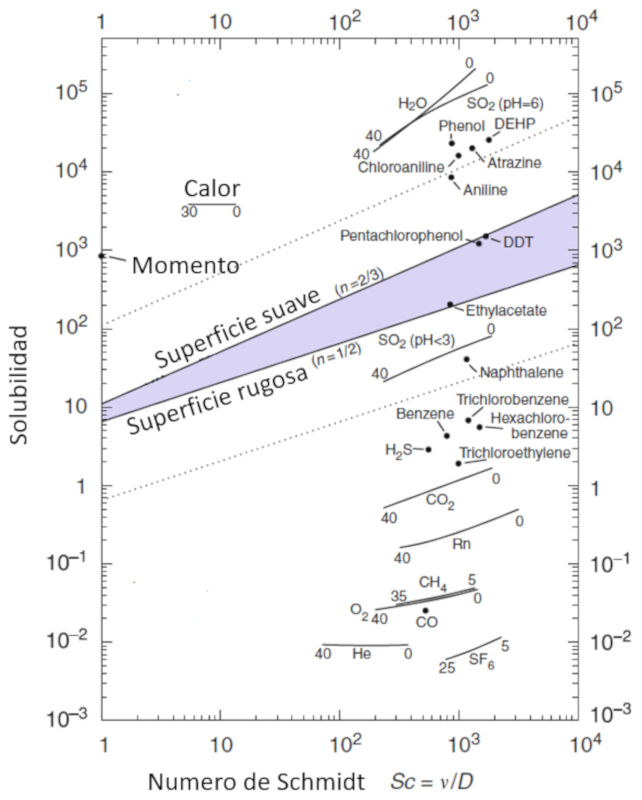
Ocean-Atmosphere Interactions of Gases and Particles, Peter S. Liss, Martin T. Johnson (eds.), Springer-Verlag Berlin Heidelberg

ID:(12245, 0)

Concepto

>Top

La velocidad de transferencia del gas en el agua ($k_w$) puede ser modelada utilizando datos medidos. En primer lugar, depende de la velocidad a la cual el sistema remueve el carbono de la interfaz aire-agua, lo que hace que la velocidad de transporte sea proporcional a la velocidad relativa entre ambos medios.

En segundo lugar, se presenta un efecto de la movilidad de los iones, que puede describirse mediante el número de Schmidt ($Sc$), representando la relación entre la difusión del impulso y las partículas. Sin embargo, esta dependencia no es lineal y está influenciada por un factor exponente de Schmidt ($n$) que varía entre -1/2 y -2/3 según la rugosidad de la superficie.

Finalmente, la velocidad de transferencia del gas en el agua ($k_w$) también depende de una el factor beta del transporte aire a agua de CO2 ($\beta$), que a su vez está determinada por el nivel de rugosidad de la superficie.

En resumen, la velocidad de transferencia del gas en el agua ($k_w$) del gas se describe en función de el velocidad del agua ($u_w$), el velocidad del aire ($u_a$), el número de Schmidt ($Sc$), el factor beta del transporte aire a agua de CO2 ($\beta$) y exponente de Schmidt ($n$) de la siguiente manera:

ID:(15652, 0)

Top

>Top

Parámetros

$C_b$

C_b

Concentración de gas en el agua

$C_0$

C_0

Concentración de gas en el aire

$C_z$

C_z

Concentración en la profundidad $z$

$C_0$

C_0

Concentración en la superficie

$D$

D

Constante de difusión en masa acuosa

m/s^2

$D_C$

D_C

Constante de transmisión de concentración

-

$F_a$

F_a

Densidad de flujo de gases atmósfera a océano

1/m^2s

$\rho$

rho

Densidad en capa de masa acuosa

kg/m^3

$\Delta p_{gas}$

Dp_gas

Diferencia de presión parcial del gas entre agua y aire

Pa

$n$

n

Exponente de Schmidt

-

$\beta$

beta

Factor beta del transporte aire a agua de CO2

-

$C$

C

Flujo de concentración

$\delta_c$

delta_c

Grosor de la capa superficial

m

$\delta_{\eta}$

delta_eta

Grosor de la capa viscosa

m

$Sc$

Sc

Número de Schmidt

-

$\alpha$

alpha

Solubilidad del gas

-

$k$

k

Velocidad de transferencia

m/s

$k_a$

k_a

Velocidad de transferencia del gas en el aire

m/s

$u_w$

u_w

Velocidad del agua

m/s

$U_z$

U_z

Velocidad del agua en la profundidad $z$

m/s

$u_a$

u_a

Velocidad del aire

m/s

$\eta$

eta

Viscosidad en masa acuosa

Pa s

Variables

$C_{w,0}$

C_w0

Concentración del gas en el agua

1/m^3

$C_a$

C_a

Concentración del gas en la atmosfera

1/m^3

$k_w$

k_w

Velocidad de transferencia del gas en el agua

m/s

Cálculos

• Método alternativo
• Método tradicional
• Estrategia
• 2D
• 3D

Ecuación

Número

Primero, seleccione la ecuación: a , luego, seleccione la variable: a

---

Cálculos

Símbolo

Ecuación

Resuelto

Traducido

Cálculos

Símbolo

Ecuación

Resuelto

Traducido

Variable Dado Calcule Objetivo : Ecuación A utilizar

Ecuaciones

ID:(15641, 0)

Ecuación

>Top, >Modelo

Dado que el flujo difusivo $F$ puede ser modelado mediante la ley de Fick:

Podemos establecer una relación entre la velocidad de transferencia $k$ y la diferencia de concentración $\Delta C$ de la siguiente manera:

$F_a =- k_a \Delta p_{gas}$

Condiciones

Variables

$F_a$

Densidad de flujo de gases atmósfera a océano

$1/m^2s$

9400

$\Delta p_{gas}$

Diferencia de presión parcial del gas entre agua y aire

$Pa$

9404

$k_a$

Velocidad de transferencia del gas en el aire

$m/s$

9407

Relación

Desarrollo

El flujo difusivo $F$ es descrito por la ley de Fick:

$F = - D \displaystyle\frac{d C }{d t }$

donde $D$ es la constante de difusión y $dC/dx$ es el gradiente de concentración. Si definimos una velocidad de transferencia de la siguiente manera:

$k_a = \displaystyle\frac{ D }{ \delta_c }$

podemos establecer una ecuación de flujo de la forma:

$F_a =- k_a \Delta p_{gas}$

ID:(12226, 0)

Ecuación

>Top, >Modelo

Con el modelo de similitud de Monin-Obukhov (MOST), es posible estimar el flujo de elementos, como los gases, teniendo en cuenta el desplazamiento de la superficie y un coeficiente de transferencia, que se expresa de la siguiente manera:

$C = D_C U_z ( C_z - C_0 )$

Condiciones

Variables

$C_z$

Concentración en la profundidad $z$

$1/m^3$

9429

$C_0$

Concentración en la superficie

$1/m^3$

9428

$D_C$

Constante de transmisión de concentración

$-$

10066

$C$

Flujo de concentración

$kg/m^2s$

10067

$U_z$

Velocidad del agua en la profundidad $z$

$m/s$

9421

Relación

Desarrollo

En el modelo de similitud de Monin-Obukhov (MOST), se estima el flujo de elementos como gases mediante la diferencia de concentraciones entre el aire y el agua, representada por

$C_z - C_0$

y se calcula el flujo utilizando el coeficiente de transferencia $D_C$ y la velocidad de la superficie $U_z$, de la siguiente manera:

$C = D_C U_z ( C_z - C_0 )$

De esta forma, se obtiene el flujo estimado de los elementos entre el aire y el agua.

ID:(12224, 0)

Ecuación

>Top, >Modelo

La diferencia de concentración entre la concentración del gas en la atmosfera ($C_a$) y la concentración del gas en el agua ($C_{w,0}$) depende de la solubilidad del gas ($\alpha$). Por lo tanto, se establece la siguiente relación:

$C_w = \alpha C_a$

Condiciones

Variables

$C_w$

Concentración del gas en el agua

$1/m^3$

9415

$C_a$

Concentración del gas en la atmosfera

$1/m^3$

9416

$\alpha$

Solubilidad del gas

$-$

9406

Relación

ID:(12235, 0)

Ecuación

>Top, >Modelo

La velocidad de transferencia de una cantidad $k$ se define como el flujo $F$ dividido por la diferencia de concentración entre los dos medios, representada por.

$C_0-C_b$

Por lo tanto, se puede expresar como:

$k =\displaystyle\frac{ F }{ C_0 - C_b }$

Condiciones

Variables

$C_b$

Concentración de gas en el agua

$1/m^3$

9401

$C_0$

Concentración de gas en el aire

$1/m^3$

9402

$F$

Densidad de flujo de gases atmósfera a océano

$1/m^2s$

9400

$k$

Velocidad de transferencia

$m/s$

9403

Relación

ID:(12213, 0)

Ecuación

>Top, >Modelo

La velocidad de transferencia del gas en el aire ($k_a$) se puede estimar a partir de la ley de Fick, comparando el constante de difusión en masa acuosa ($D$) con el grosor de la capa superficial ($\delta_c$) de la siguiente manera:

$k_a = \displaystyle\frac{ D }{ \delta_c }$

Condiciones

Variables

$D$

Constante de difusión en masa acuosa

$m^2/s$

9414

$\delta_c$

Grosor de la capa superficial

$m$

9430

$k_a$

Velocidad de transferencia del gas en el aire

$m/s$

9407

Relación

ID:(12227, 0)

Ecuación

>Top, >Modelo

La velocidad de transferencia del CO2 desde la atmósfera al agua se puede modelar utilizando una ecuación similar a la regla general

En este modelo, la diferencia de concentración se reemplaza por la diferencia de presión parcial del gas y la solubilidad $\alpha$. del CO2. La ecuación se expresa de la siguiente manera:

$F_w = k_w \Delta p_{gas}$

Condiciones

Variables

$\Delta p_{gas}$

Diferencia de presión parcial del gas entre agua y aire

$Pa$

9404

$k_w$

Velocidad de transferencia del gas en el agua

$m/s$

9405

Relación

Desarrollo

Si se considera el flujo del gas $F$ y la velocidad de transporte $k$ con la relación genérica

$k =\displaystyle\frac{ F }{ C_0 - C_b }$

Si se reemplaza la diferencia de concentraciones $C_0-C_b$ con la diferencia de la presión parcial del gas usando la solubilidad $\alpha$ de modo que:

$C_0 - C_b = \alpha \Delta p_{CO2}$

se obtiene

$F_w = k_w \Delta p_{gas}$

ID:(12214, 0)

Ecuación

>Top, >Modelo

La velocidad de transferencia del gas en el agua ($k_w$) del gas se describe en función de el velocidad del agua ($u_w$), el velocidad del aire ($u_a$), el número de Schmidt ($Sc$), el factor beta del transporte aire a agua de CO2 ($\beta$) y exponente de Schmidt ($n$) de la siguiente manera:

$k_w = ( u_a - u_w ) \beta Sc ^ n$

Condiciones

Variables

$n$

Exponente de Schmidt

$-$

9926

$\beta$

Factor beta del transporte aire a agua de CO2

$-$

9409

$Sc$

Número de Schmidt

$-$

9410

$k_w$

Velocidad de transferencia del gas en el agua

$m/s$

9405

$u_w$

Velocidad del agua

$m/s$

9437

$u_a$

Velocidad del aire

$m/s$

9408

Relación

ID:(12215, 0)

Ecuación

>Top, >Modelo

El número de Schmidt establece una relación entre lo que es la difusión viscosa

con lo que es la difusión de partículas

.

La primera en igual a la viscosidad partida por la densidad mientras que la segunda corresponde a la constante de difusión. Por ello se define como

$Sc =\displaystyle\frac{ \eta }{ \rho D }$

Condiciones

Variables

$D$

Constante de difusión en masa acuosa

$m^2/s$

9414

$\rho$

Densidad en capa de masa acuosa

$kg/m^3$

9413

$Sc$

Número de Schmidt

$-$

9410

$\eta$

Viscosidad en masa acuosa

$Pa s$

9412

Relación

ID:(12216, 0)

Ecuación

>Top, >Modelo

El grosor de la superficie y de la capa viscosas son proposicionales siendo la constante una función de la constante difusión, viscosidad y densidad.

Por ello con es

$\delta_c = \sqrt{\displaystyle\frac{ \rho D }{ \eta }} \delta_{\eta}$

Condiciones

Variables

$D$

Constante de difusión en masa acuosa

$m^2/s$

9414

$\rho$

Densidad en capa de masa acuosa

$kg/m^3$

9413

$\delta_c$

Grosor de la capa superficial

$m$

9430

$\delta_{\eta}$

Grosor de la capa viscosa

$m$

9431

$\eta$

Viscosidad en masa acuosa

$Pa s$

9412

Relación

Desarrollo

None

ID:(12229, 0)