Utilisateur:
Échange de particules
Storyboard 
L'échange de substances entre l'atmosphère et l'océan peut inclure des particules. Ceci est particulièrement pertinent lors de l'étude du transfert de molécules de CO2 de l'atmosphère vers l'océan.
Ocean-Atmosphere Interactions of Gases and Particles, Peter S. Liss, Martin T. Johnson (eds.). Springer, 2014
Chapter: Transfer Across the Air-Sea Interface
ID:(1630, 0)
Diffusion de CO2
Description
Le CO2 est absorbé par les océans, ce qui contribue à atténuer son effet sur l'atmosphère et à retarder le changement climatique. Cependant, les processus impliqués sont plus complexes et comprennent :
- Échange gazeux avec l\'atmosphère : L\'océan et l\'atmosphère sont en constante échange de CO2 par diffusion des gaz. Le CO2 atmosphérique se dissout à la surface de l\'océan et forme de l\'acide carbonique (H2CO3), qui se dissocie ensuite en ions hydrogène (H+) et en bicarbonate (HCO3-). Ce processus aide à équilibrer les niveaux de CO2 entre l\'océan et l\'atmosphère.
- Photosynthèse et respiration : Les organismes marins tels que le phytoplancton et les algues réalisent la photosynthèse et absorbent le CO2 de l\'eau pour produire de la matière organique et libérer de l\'oxygène. Ce processus, appelé fixation du carbone, contribue à extraire le CO2 de l\'océan. Cependant, les organismes marins respirent également, ce qui signifie qu\'ils libèrent du CO2 dans l\'eau lors de la décomposition de la matière organique.
- Circulation océanique : L\'océan est caractérisé par sa circulation mondiale, au cours de laquelle les courants transportent de l\'eau riche en CO2 de la surface vers les profondeurs et vice versa. Cela contribue à la distribution et au mélange du CO2 dans l\'ensemble de l\'océan, permettant aux eaux profondes de stocker d\'importantes quantités de CO2 dissous.
- Sédimentation et enfouissement : Une partie de la matière organique produite par les organismes marins, y compris le CO2 capturé par la photosynthèse, peut s\'enfoncer et être enfouie au fond de l\'océan. Au fil du temps géologique, les sédiments s\'accumulent et le carbone organique est enfoui, pouvant être stocké dans le fond marin pendant de très longues périodes.
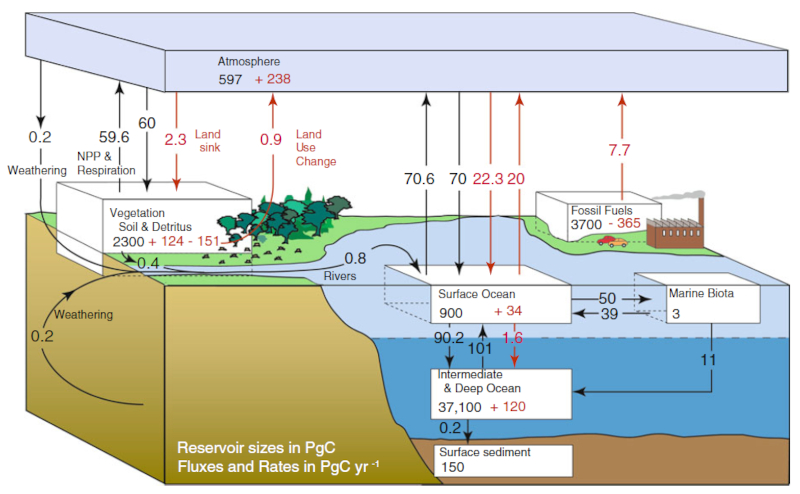
Flux de carbone annuel en PgC/an. Les chiffres en noir représentent la révolution préindustrielle, en rouge les augmentations liées à la révolution industrielle. Ocean-Atmosphere Interactions of Gases and Particles, Peter S. Liss Martin T. Johnson (Editors), Springer, 2014
Selon la zone et l'époque de la planète, il y a une plus grande concentration de carbone dans l'atmosphère que dans l'océan ou vice versa, définissant ainsi si le flux de carbone se fait de l'air vers l'eau ou vice versa.
ID:(12297, 0)
Vitesse de transfert et vitesse relative
Description
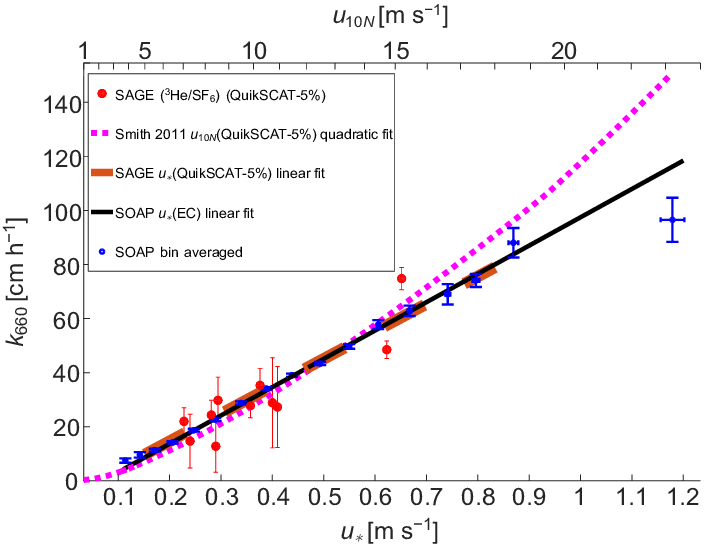
Dans une première approximation, la dépendance de a taux de transfert de gaz dans l'eau ($k_w$) par rapport à la vitesse relative, calculée en soustrayant ($$) de ($$), est proportionnelle à
$k_w \propto u_a - u_w$
comme observé dans le graphique :
ID:(12298, 0)
Vitesse de transfert et nombre de Schmidt
Description
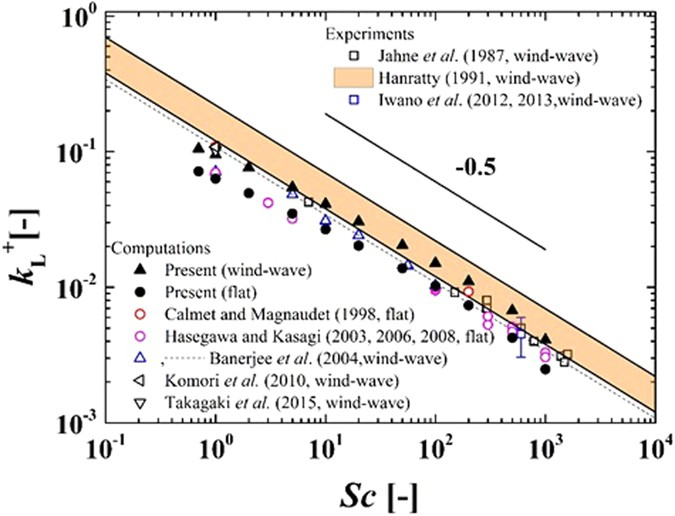
La relation entre a taux de transfert de gaz dans l'eau ($k_w$) est inversement proportionnelle à Le numéro de Schmidt ($Sc$), donc elle est exprimée comme étant proportionnelle à ce nombre élevé à ($$), qui est négatif :
$k_w\propto Sc^n$
ceci est représenté avec ($$) égal à -0.5 :
ID:(12299, 0)
Solubilité en fonction du nombre de Schmidt
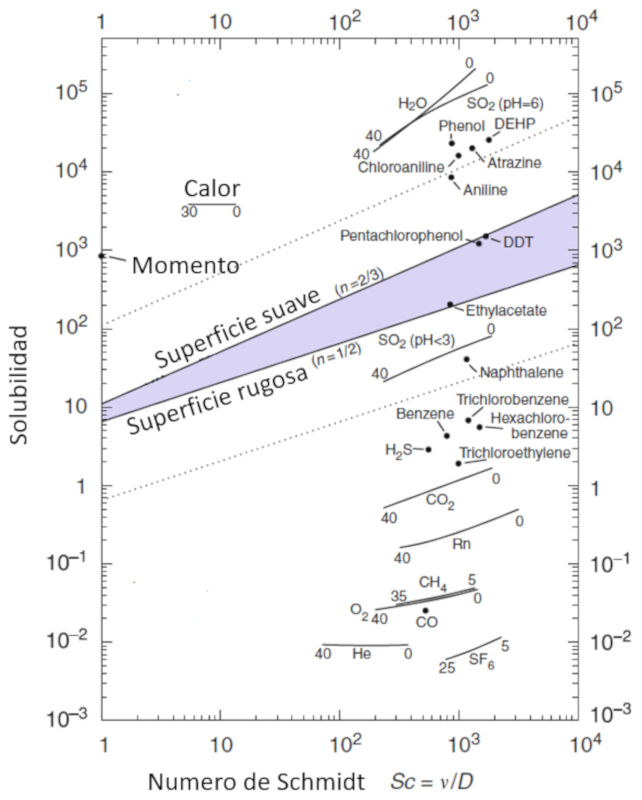
Concept
La mobilité des molécules, représentée par a solubilité du gaz ($\alpha$), est une fonction de la concentration de particules, décrite par le numéro de Schmidt ($Sc$), qui à son tour est calculée à partir de ($$), ($$) et ($$) selon l'équation suivante :
| $ Sc =\displaystyle\frac{ \eta }{ \rho D }$ |
Cette relation est illustrée dans le schéma suivant :
ID:(12245, 0)
Échange de CO2, vitesse de l'eau
Concept
A taux de transfert de gaz dans l'eau ($k_w$) peut être modélisé en utilisant des données mesurées. Tout d'abord, il dépend de la vitesse à laquelle le système élimine le carbone de l'interface air-eau, ce qui rend la vitesse de transport proportionnelle à la vitesse relative entre les deux milieux.
Deuxièmement, il y a un effet de la mobilité des ions, qui peut être décrit par le numéro de Schmidt ($Sc$), représentant la relation entre la diffusion de l'impulsion et les particules. Cependant, cette dépendance n'est pas linéaire et est influencée par un facteur ($$) qui varie entre -1/2 et -2/3 en fonction de la rugosité de la surface.
Enfin, a taux de transfert de gaz dans l'eau ($k_w$) dépend également de ($$), qui est à son tour déterminé par le niveau de rugosité de la surface.
En résumé, le gaz a taux de transfert de gaz dans l'eau ($k_w$) est décrit en fonction de ($$), ($$), le numéro de Schmidt ($Sc$), ($$) et ($$) de la manière suivante :
| $ k_w = ( u_a - u_w ) \beta Sc ^ n $ |
ID:(15652, 0)
Modèle
Top
Paramètres
Variables
Calculs
à 
, puis, sélectionnez la variable: 
à 
Calculs
Calculs
Variable 
Donnée Calculer 
Cible : Équation À utiliser 
Équations
$ C = D_C U_z ( C_z - C_0 )$
C = D_C * U_z *( C_z - C_0 )
$ C_w = \alpha C_a $
C_w = alpha * C_a
$ \delta_c = \sqrt{\displaystyle\frac{ \rho D }{ \eta }} \delta_{\eta}$
delta_c =sqrt( D * rho / eta )* delta_eta
$ F_a =- k_a \Delta p_{gas} $
F_a =- k_a * Dp_gas
$ F_w = k_w \Delta p_{gas} $
F_w = k_w * Dp_gas
$ k =\displaystyle\frac{ F }{ C_0 - C_b }$
k = F /( C_0 - C_b )
$ k_a = \displaystyle\frac{ D }{ \delta_c }$
k_a = D / delta_c
$ k_w = ( u_a - u_w ) \beta Sc ^ n $
k_w = ( u_a - u_w )* beta * Sc ^ n
$ Sc =\displaystyle\frac{ \eta }{ \rho D }$
Sc = eta /( rho * D )
ID:(15641, 0)
Flux diffus avec taux de transfert
Équation
Étant donné que le fluxe diffusif $F$ peut être modélisé à l\'aide de la loi de Fick :
| $ F = - D \displaystyle\frac{d C }{d t }$ |
Nous pouvons établir une relation entre la vitesse de transfert $k$ et la différence de concentration $\Delta C$ de la manière suivante :
| $ F_a =- k_a \Delta p_{gas} $ |
Le flux diffusif $F$ est décrit par la loi de Fick :
| $ F = - D \displaystyle\frac{d C }{d t }$ |
où $D$ est la constante de diffusion et $dC/dx$ est le gradient de concentration. En définissant une vitesse de transfert comme suit :
| $ k_a = \displaystyle\frac{ D }{ \delta_c }$ |
nous pouvons établir une équation de flux de la forme :
| $ F_a =- k_a \Delta p_{gas} $ |
ID:(12226, 0)
Profil de concentration dans la couche de surface (MOST)
Équation
En utilisant le modèle de similarité de Monin-Obukhov (MOST), il est possible d'estimer le flux d'éléments tels que les gaz en tenant compte du déplacement de la surface et d\'un coefficient de transfert, qui s\'exprime de la manière suivante:
| $ C = D_C U_z ( C_z - C_0 )$ |
Dans le modèle de similarité de Monin-Obukhov (MOST), le flux d'éléments tels que les gaz est estimé en tenant compte de la différence de concentrations entre l'air et l\'eau, représentée par
$C_z - C_0$
et le flux est calculé en utilisant le coefficient de transfert $D_C$ et la vitesse de surface $U_z$, de la manière suivante :
| $ C = D_C U_z ( C_z - C_0 )$ |
Cela permet d\'estimer le flux des éléments entre l\'air et l\'eau.
ID:(12224, 0)
Relations de concentration de surface
Équation
Le gradient de concentration entre a concentration de gaz dans l'atmosphère ($C_a$) et a concentration de gaz dans l'eau ($C_{w,0}$) dépend de a solubilité du gaz ($\alpha$). Par conséquent, la relation suivante est établie :
| $ C_w = \alpha C_a $ |
ID:(12235, 0)
Transport d\'une quantité
Équation
La vitesse de transfert d\'une quantité $k$ est définie comme le flux $F$ divisé par la différence de concentration entre les deux milieux, représentée par
$C_0-C_b$
Par conséquent, elle peut être exprimée comme suit:
| $ k =\displaystyle\frac{ F }{ C_0 - C_b }$ |
ID:(12213, 0)
Vitesse de transfert
Équation
A taux de transfert de gaz dans l'air ($k_a$) peut être estimé à partir de la loi de Fick, en comparant ($$) avec ($$) de la manière suivante :
| $ k_a = \displaystyle\frac{ D }{ \delta_c }$ |
ID:(12227, 0)
Échange de CO2
Équation
La vitesse de transfert du CO2 de l\'atmosphère vers l\'eau peut être modélisée en utilisant une équation similaire à la règle générale
| $ k =\displaystyle\frac{ F }{ C_0 - C_b }$ |
Dans ce modèle, la différence de concentration est remplacée par la différence de pression partielle du gaz et sa solubilité $\alpha$. L\'équation peut être exprimée de la manière suivante:
| $ F_w = k_w \Delta p_{gas} $ |
Si nous considérons le flux de gaz $F$ et la vitesse de transport $k$, selon la relation générale :
| $ k =\displaystyle\frac{ F }{ C_0 - C_b }$ |
En remplaçant la différence de concentration $C_0 - C_b$ par la différence de pression partielle du gaz en utilisant la solubilité $\alpha$, nous obtenons :
$C_0 - C_b = \alpha \Delta p_{CO2}$
nous pouvons alors obtenir :
| $ F_w = k_w \Delta p_{gas} $ |
ID:(12214, 0)
Échange de CO2, vitesse de l'eau
Équation
Le paramètre du gaz a taux de transfert de gaz dans l'eau ($k_w$) est décrit en fonction de ($$), ($$), le numéro de Schmidt ($Sc$), ($$) et ($$) comme suit :
| $ k_w = ( u_a - u_w ) \beta Sc ^ n $ |
ID:(12215, 0)
Le nombre de Schmidt Sc
Équation
Le nombre de Schmidt établit une relation entre la diffusion visqueuse
| $ D_p \equiv \displaystyle\frac{ \eta }{ \rho }$ |
et la diffusion des particules
| $ D_N \equiv \mu k_B T $ |
.
La diffusion visqueuse est égale à la viscosité divisée par la densité, tandis que la diffusion des particules correspond à la constante de diffusion. Par conséquent, il est défini comme suit :
| $ Sc =\displaystyle\frac{ \eta }{ \rho D }$ |
ID:(12216, 0)