Benützer:
Partikelaustausch
Storyboard 
Der Austausch von Substanzen zwischen der Atmosphäre und dem Ozean kann Partikel einschließen. Dies ist besonders relevant, wenn man den Übergang von CO2-Molekülen aus der Atmosphäre in den Ozean untersucht.
Ocean-Atmosphere Interactions of Gases and Particles, Peter S. Liss, Martin T. Johnson (eds.). Springer, 2014
Chapter: Transfer Across the Air-Sea Interface
ID:(1630, 0)
CO2-Diffusion
Beschreibung
Die Absorption von CO2 durch die Ozeane trägt dazu bei, die Auswirkungen dieses Gases in der Atmosphäre zu mildern und verzögert somit den Klimawandel. Die involvierten Prozesse sind jedoch komplexer und umfassen:
- Gasausstausch mit der Atmosphäre: Der Ozean und die Atmosphäre tauschen ständig CO2 durch Gasaustausch aus. Das atmosphärische CO2 löst sich in der Oberfläche des Ozeans auf und bildet Kohlensäure (H2CO3), die dann in Wasserstoffionen (H+) und Bicarbonationen (HCO3-) dissoziiert. Dieser Prozess hilft, das Gleichgewicht der CO2-Konzentrationen zwischen dem Ozean und der Atmosphäre zu halten.
- Photosynthese und Atmung: Marine Organismen wie Phytoplankton und Algen betreiben Photosynthese und nehmen CO2 aus dem Wasser auf, um organische Substanz zu produzieren und Sauerstoff freizusetzen. Dieser Prozess, als Kohlenstofffixierung bekannt, hilft, CO2 aus dem Ozean zu entfernen. Andererseits atmen marine Organismen auch, was bedeutet, dass sie CO2 ins Wasser abgeben während der Zersetzung organischer Substanz.
- Ozeanzirkulation: Der Ozean zeichnet sich durch seine globale Zirkulation aus, bei der Strömungen CO2-reiches Wasser von der Oberfläche in die Tiefe und umgekehrt transportieren. Dies trägt zur Verteilung und Durchmischung von CO2 im gesamten Ozean bei und ermöglicht es den Tiefenwassern, große Mengen an gelöstem CO2 zu speichern.
- Sedimentation und Einbettung: Ein Teil der von marinen Organismen produzierten organischen Substanz, einschließlich des durch Photosynthese aufgenommenen CO2, kann zum Meeresboden sinken. Wenn sich Sedimente über geologische Zeiträume ansammeln, kann der organische Kohlenstoff eingebettet und über lange Zeiträume im Meeresboden gespeichert werden.
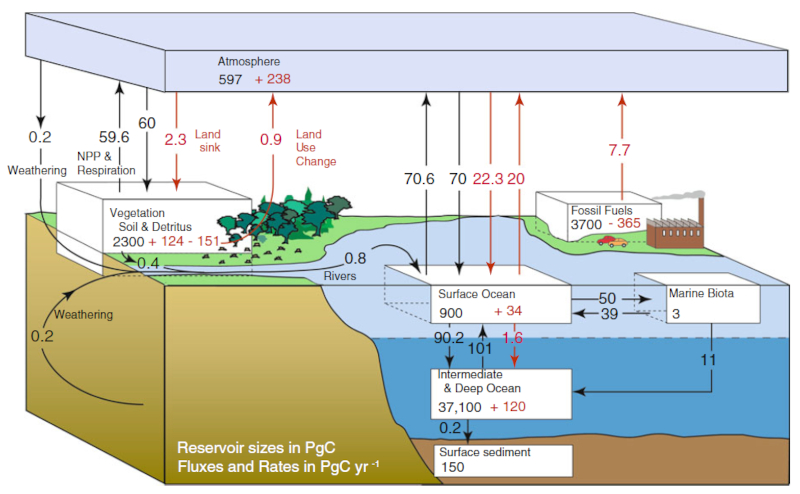
Jährlicher Kohlenstofffluss in PgC/Jahr. Die schwarzen Zahlen stehen für die vorindustrielle Revolution, die roten Zahlen für die Steigerungen im Zusammenhang mit der industriellen Revolution. Ocean-Atmosphere Interactions of Gases and Particles, Peter S. Liss Martin T. Johnson (Editors), Springer, 2014
Abhängig von der Region und der Zeit auf dem Planeten gibt es in der Atmosphäre eine höhere Kohlenstoffkonzentration als im Ozean oder umgekehrt, und bestimmt so, ob der Kohlenstofffluss von der Luft ins Wasser oder umgekehrt erfolgt.
ID:(12297, 0)
Übertragungsrate und relative Geschwindigkeit
Beschreibung
In einer ersten Näherung ist die Abhängigkeit von die Gasübertragungsrate in Wasser ($k_w$) in Bezug auf die relative Geschwindigkeit, die durch Subtraktion von der Velocidad del agua ($u_w$) von der Velocidad del aire ($u_a$) berechnet wird, proportional zu
$k_w \propto u_a - u_w$
wie im Diagramm dargestellt:
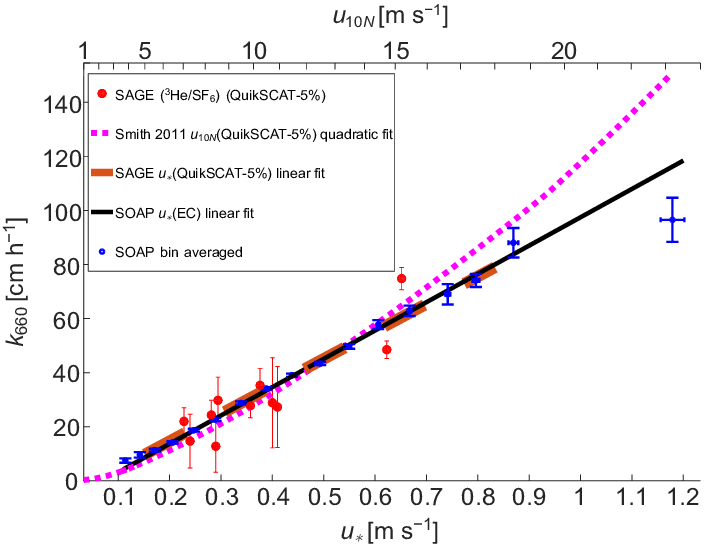
ID:(12298, 0)
Übertragungsrate und Schmidt-Zahl
Beschreibung
Die Beziehung zwischen die Gasübertragungsrate in Wasser ($k_w$) ist indirekt proportional zu der Schmidt-Nummer ($Sc$), daher wird sie als proportional zu dieser Zahl, hoch Exponente de Schmidt ($n$), ausgedrückt, die negativ ist:
$k_w\propto Sc^n$
was mit Exponente de Schmidt ($n$) gleich -0,5 dargestellt wird:
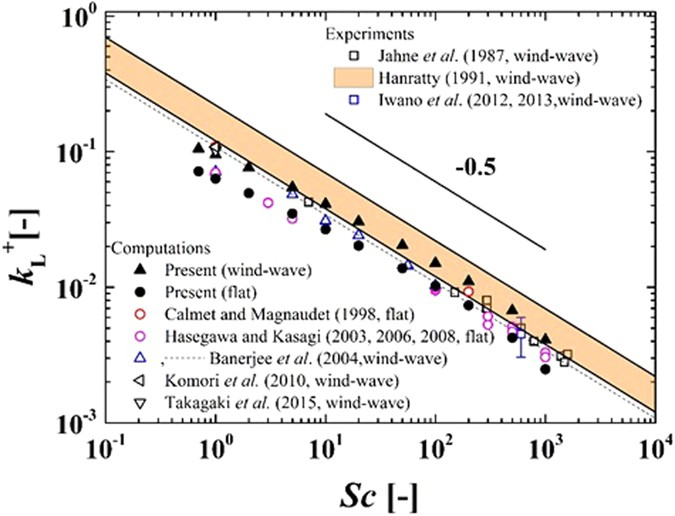
ID:(12299, 0)
Löslichkeit als Funktion der Schmidt-Zahl
Konzept
Die Beweglichkeit von Molekülen, dargestellt durch die Gaslöslichkeit ($\alpha$), wird als Funktion der Partikelkonzentration modelliert, die durch der Schmidt-Nummer ($Sc$) charakterisiert ist. Diese wird wiederum aus den Parametern der Viscosidad en masa acuosa ($\eta$), der Densidad en capa de masa acuosa ($\rho$) und der Constante de difusión en masa acuosa ($D$) mithilfe des folgenden Ausdrucks berechnet:
| $ Sc =\displaystyle\frac{ \eta }{ \rho D }$ |
Diese Beziehung wird im folgenden Diagramm visualisiert:
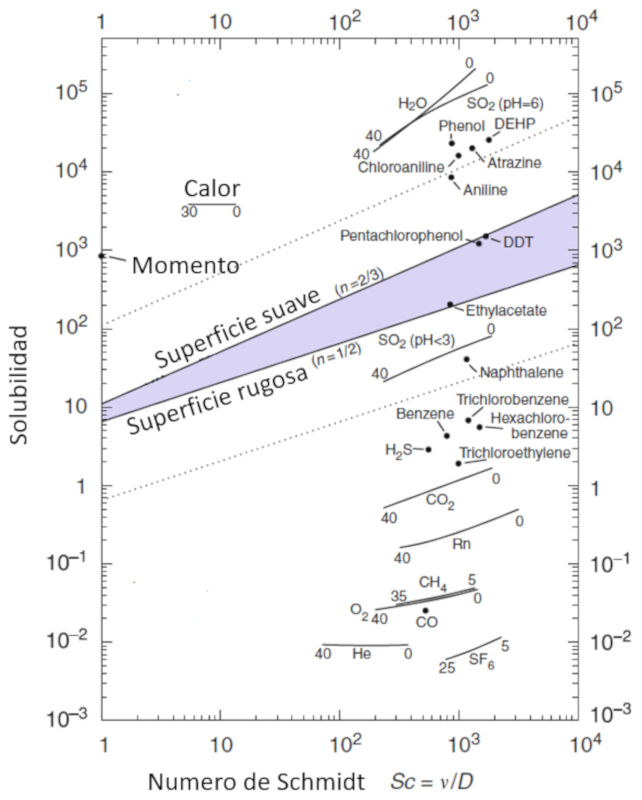
Ocean-Atmosphere Interactions of Gases and Particles, Peter S. Liss, Martin T. Johnson (eds.), Springer-Verlag Berlin Heidelberg
ID:(12245, 0)
CO2-Austausch, Geschwindigkeit aus Wasser
Konzept
Die Gasübertragungsrate in Wasser ($k_w$) kann mithilfe gemessener Daten modelliert werden. Erstens hängt es von der Geschwindigkeit ab, mit der das System Kohlenstoff von der Luft-Wasser-Grenzfläche entfernt, wodurch die Transportgeschwindigkeit proportional zur Relativgeschwindigkeit zwischen den beiden Medien wird.
Zweitens gibt es einen Effekt der Ionenmobilität, der durch der Schmidt-Nummer ($Sc$) beschrieben werden kann und die Beziehung zwischen Impulsdiffusion und Partikeln darstellt. Diese Abhängigkeit ist jedoch nicht linear und wird durch einen Faktor Exponente de Schmidt ($n$) beeinflusst, der je nach Oberflächenrauheit zwischen -1/2 und -2/3 variiert.
Schließlich hängt die Gasübertragungsrate in Wasser ($k_w$) auch von der Factor beta del transporte aire a agua de CO2 ($\beta$) ab, die wiederum durch das Rauheitsniveau der Oberfläche bestimmt wird.
Zusammenfassend wird das Gas die Gasübertragungsrate in Wasser ($k_w$) als Funktion von der Velocidad del agua ($u_w$), der Velocidad del aire ($u_a$), der Schmidt-Nummer ($Sc$), der Factor beta del transporte aire a agua de CO2 ($\beta$) und Exponente de Schmidt ($n$) wie folgt beschrieben:
| $ k_w = ( u_a - u_w ) \beta Sc ^ n $ |
ID:(15652, 0)
Modell
Top
Parameter
Variablen
Berechnungen
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden 
Gleichungen
$ C = D_C U_z ( C_z - C_0 )$
C = D_C * U_z *( C_z - C_0 )
$ C_w = \alpha C_a $
C_w = alpha * C_a
$ \delta_c = \sqrt{\displaystyle\frac{ \rho D }{ \eta }} \delta_{\eta}$
delta_c =sqrt( D * rho / eta )* delta_eta
$ F_a =- k_a \Delta p_{gas} $
F_a =- k_a * Dp_gas
$ F_w = k_w \Delta p_{gas} $
F_w = k_w * Dp_gas
$ k =\displaystyle\frac{ F }{ C_0 - C_b }$
k = F /( C_0 - C_b )
$ k_a = \displaystyle\frac{ D }{ \delta_c }$
k_a = D / delta_c
$ k_w = ( u_a - u_w ) \beta Sc ^ n $
k_w = ( u_a - u_w )* beta * Sc ^ n
$ Sc =\displaystyle\frac{ \eta }{ \rho D }$
Sc = eta /( rho * D )
ID:(15641, 0)
Flujo difuso con la velocidad de transferencia
Gleichung
Da der diffusive Fluss $F$ mit dem Gesetz von Fick modelliert werden kann:
| $ F = - D \displaystyle\frac{d C }{d t }$ |
können wir eine Beziehung zwischen der Transfergeschwindigkeit $k$ und der Konzentrationsdifferenz $\Delta C$ wie folgt herstellen:
| $ F_a =- k_a \Delta p_{gas} $ |
Der diffusive Fluss $F$ wird durch das Fick\'sche Gesetz beschrieben:
| $ F = - D \displaystyle\frac{d C }{d t }$ |
wobei $D$ die Diffusionskonstante und $dC/dx$ das Konzentrationsgefälle ist. Wenn wir eine Transfergeschwindigkeit wie folgt definieren:
| $ k_a = \displaystyle\frac{ D }{ \delta_c }$ |
können wir eine Flussequation der Form definieren:
| $ F_a =- k_a \Delta p_{gas} $ |
ID:(12226, 0)
Konzentrationsprofil in der Oberflächenschicht (MOST)
Gleichung
Mit dem Modell der Monin-Obukhov-Ähnlichkeitstheorie (MOST) kann der Fluss von Elementen wie Gasen unter Berücksichtigung der Verschiebung der Oberfläche und eines Übertragungskoeffizienten geschätzt werden. Dies wird wie folgt ausgedrückt:
| $ C = D_C U_z ( C_z - C_0 )$ |
Im Modell der Monin-Obukhov-Ähnlichkeitstheorie (MOST) wird der Fluss von Elementen wie Gasen geschätzt, indem die Konzentrationsdifferenz zwischen Luft und Wasser berücksichtigt wird, dargestellt durch
$C_z - C_0$
und der Fluss wird unter Verwendung des Übertragungskoeffizienten $D_C$ und der Oberflächengeschwindigkeit $U_z$ berechnet, wie folgt:
| $ C = D_C U_z ( C_z - C_0 )$ |
Damit kann der Fluss der Elemente zwischen Luft und Wasser abgeschätzt werden.
ID:(12224, 0)
Beziehungen der Oberflächenkonzentration
Gleichung
Der Konzentrationsunterschied zwischen die Gaskonzentration in der Atmosphäre ($C_a$) und die Gaskonzentration im Wasser ($C_{w,0}$) hängt von die Gaslöslichkeit ($\alpha$) ab. Daher wird die folgende Beziehung hergestellt:
| $ C_w = \alpha C_a $ |
ID:(12235, 0)
Transport einer Menge
Gleichung
Die Transfergeschwindigkeit einer Größe $k$ wird als Fluss $F$ geteilt durch die Konzentrationsdifferenz zwischen den beiden Medien definiert, dargestellt als
$C_0-C_b$
Daher kann sie wie folgt ausgedrückt werden:
| $ k =\displaystyle\frac{ F }{ C_0 - C_b }$ |
ID:(12213, 0)
Übertragungsgeschwindigkeit
Gleichung
Die Gasübertragungsrate in Luft ($k_a$) kann aus dem Fick'schen Gesetz geschätzt werden, indem der Constante de difusión en masa acuosa ($D$) mit der Grosor de la capa superficial ($\delta_c$) wie folgt verglichen wird:
| $ k_a = \displaystyle\frac{ D }{ \delta_c }$ |
ID:(12227, 0)
CO2-Austausch
Gleichung
Die Übertragungsgeschwindigkeit von CO2 von der Atmosphäre auf das Wasser kann mit einer Gleichung modelliert werden, die der allgemeinen Regel ähnelt
| $ k =\displaystyle\frac{ F }{ C_0 - C_b }$ |
In diesem Modell wird der Konzentrationsunterschied durch den Unterschied des Partialdrucks des Gases und seiner Löslichkeit $\alpha$ ersetzt. Die Gleichung kann wie folgt ausgedrückt werden:
| $ F_w = k_w \Delta p_{gas} $ |
Wenn wir den Gasfluss $F$ und die Transportgeschwindigkeit $k$ betrachten, basierend auf der allgemeinen Beziehung:
| $ k =\displaystyle\frac{ F }{ C_0 - C_b }$ |
Wenn wir die Konzentrationsdifferenz $C_0 - C_b$ durch die Differenz des Partialdrucks des Gases unter Verwendung der Löslichkeit $\alpha$ ersetzen, erhalten wir:
$C_0 - C_b = \alpha \Delta p_{CO2}$
erhalten wir:
| $ F_w = k_w \Delta p_{gas} $ |
ID:(12214, 0)
CO2-Austausch, Geschwindigkeit aus Wasser
Gleichung
Der Gasparameter die Gasübertragungsrate in Wasser ($k_w$) wird in Bezug auf der Velocidad del agua ($u_w$), der Velocidad del aire ($u_a$), der Schmidt-Nummer ($Sc$), der Factor beta del transporte aire a agua de CO2 ($\beta$) und Exponente de Schmidt ($n$) wie folgt beschrieben:
| $ k_w = ( u_a - u_w ) \beta Sc ^ n $ |
ID:(12215, 0)
Schmidts Zahl Sc
Gleichung
Die Schmidt-Zahl stellt eine Beziehung zwischen der viskosen Diffusion
| $ D_p \equiv \displaystyle\frac{ \eta }{ \rho }$ |
und der Partikeldiffusion
| $ D_N \equiv \mu k_B T $ |
.
Die viskose Diffusion entspricht dabei der Viskosität geteilt durch die Dichte, während die Partikeldiffusion durch die Diffusionskonstante beschrieben wird. Daher wird sie wie folgt definiert:
| $ Sc =\displaystyle\frac{ \eta }{ \rho D }$ |
ID:(12216, 0)
Oberflächendicke und viskose Schicht
Gleichung
El grosor de la superficie y de la capa viscosas son proposicionales siendo la constante una función de la constante difusión, viscosidad y densidad.
Por ello con es
| $ \delta_c = \sqrt{\displaystyle\frac{ \rho D }{ \eta }} \delta_{\eta}$ |
ID:(12229, 0)