Usuario:
Cambio de Fáse
Storyboard 
Uno de los procesos de cambio de fase es el proceso de evaporación. En el liquido absorbe energía haciendo que moléculas de este pasen al estado de gas que denominamos vapor.
Para modelar se trabaja con la ecuación de Clausius Clapeyron que permite estimar la presión del vapor en equilibrio con el liquido.
ID:(316, 0)
Cambios de fases
Variable
Uno de los fenómenos que también incluye la termodinámica es el estudio de los cambios de estado. Existen tres estados básicos, el gaseoso, el liquido y el solido.
En el caso del gas las partículas se mueven en forma casi libres e interactúan solo por choques esporádicos.
En el caso de un liquido la interacción es permanente. Pese a ello las partículas se logran desplazar sin existir uniones permanentes hacia los vecinos.
En el caso del solido las interacciones son tales que las partículas ya no se logran desplazar y solo oscilan en torno a un punto de equilibrio definido por las partículas vecinas.
El estudio de los cambios de estado trata de explicar porque el material pasa e una forma a la otra y viceversa. En el caso de la medicina dichos cambios son relevantes en procesos en que por ejemplo se evaporan o disuelven sustancias. Esto tanto para la remoción de materiales como para la reducción de temperatura como es la transpiración.
ID:(147, 0)
Caso especial del Agua
Audio
El agua es un caso especial ya que su diagrama de fase presenta una diferencia clave con respecto de la gran mayoría de materiales: la linea que separa las fases de solido y liquido tiene pendiente negativa.
Esto se debe a que el agua al pasar de solido a liquido reduce su volumen y con ello la variación de volumen $\Delta V$ resulta negativa y la pendiente en la ecuación de Clausius Clapeyron termina siendo negativa.
Esta propiedad del agua lleva a que si se le baja la temperatura cuando esta en estado liquido $(dT,negativo)$ al llegar al cambio de fase la presión se incrementa $(dp)$ mientras que en un liquido normal esta se reduce. Esto es lo que lleva a que en invierno por ejemplo
al congelarse el agua acumulada en las rendijas y grietas de rocas en las montañas genera presión lo que lleva a su ruptura y finalmente a la erosión de nuestra geografía.
al congelarse la superficie de un lago encapsula el agua del lago evitando que esta se pueda expandir para pasar a formar hielo. Esto evita que los lagos se congelen hasta el fondo preservando la vida en su interior.
ID:(146, 0)
Cambio de Fáse
Descripción
Uno de los procesos de cambio de fase es el proceso de evaporación. En el liquido absorbe energía haciendo que moléculas de este pasen al estado de gas que denominamos vapor. Para modelar se trabaja con la ecuación de Clausius Clapeyron que permite estimar la presión del vapor en equilibrio con el liquido.
Variables
Cálculos
a 
,
luego, seleccione la variable: 
a 
Cálculos
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
(ID 3200)
Con la ley de Clausius-Clapeyron, que depende de la variación de la presión ($dp$), la variación de la temperatura ($dT$), el calor latente ($L$), la variación de volumen en cambio de fase ($\Delta V$) y la temperatura absoluta ($T$) y se expresa como:
| $\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ L }{ \Delta V T }$ |
y la definici n de el calor latente molar ($l_m$), en la que el calor latente ($L$) est relacionado con la masa molar ($M_m$) de la siguiente manera:
| $ l_m \equiv\displaystyle\frac{ L }{ M_m }$ |
y el variación del volumen molar en cambio de fase ($\Delta v_m$), en la que la variación de volumen en cambio de fase ($\Delta V$) est relacionado con la masa molar ($M_m$) de la siguiente manera:
| $\Delta v_m =\displaystyle\frac{ \Delta V }{ M_m }$ |
se obtiene:
| $\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ l_m }{ \Delta v_m T }$ |
(ID 12822)
Si el diferencial de la energía libre de Gibbs ($dG$) es constante, esto significa que para la variación de la presión ($dp$) y la variación de la temperatura ($dT$), el valor de la entropía ($S$) y el volumen ($V$) en la fase 1
$dG = -S_1dT+V_1dp$
y la entropía ($S$) y el volumen ($V$) en la fase 2
$dG = -S_2dT+V_2dp$
resultan en
$\displaystyle\frac{dp}{dT}=\displaystyle\frac{S_2-S_1}{V_2-V_1}$
El cambio en la entropía ($S$) entre ambas fases corresponde a el calor latente ($L$) dividido por la temperatura absoluta ($T$):
$S_2 - S_1 =\displaystyle\frac{ L }{ T }$
Entonces, con la definici n de la variación de volumen en cambio de fase ($\Delta V$)
$\Delta V \equiv V_2 - V_1$
obtenemos
| $\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ L }{ \Delta V T }$ |
(ID 12824)
Ejemplos
(ID 15286)
Uno de los diagramas de fase m s significativos para nuestro planeta es el del agua. Este diagrama presenta las tres fases cl sicas: s lido, l quido y gas, adem s de una variedad de fases con diferentes estructuras cristalinas del hielo.
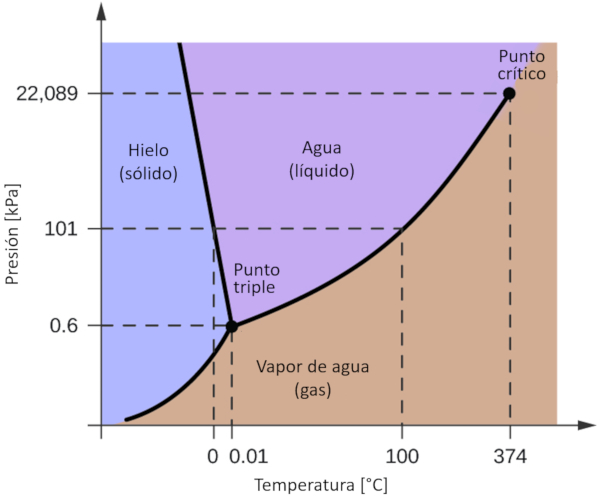
La caracter stica m s destacada en comparaci n con otros materiales es que en un rango de presi n comprendido entre 611 Pa y 209.9 MPa, el estado s lido ocupa un volumen mayor que el estado l quido. Este fen meno se refleja en el diagrama de fase como una pendiente negativa en la l nea que separa las fases s lidas (hielo con estructura hexagonal) y l quidas (agua).
(ID 836)
Si el diferencial de la energía libre de Gibbs ($dG$) es constante, esto implica que para la variación de la presión ($dp$) y la variación de la temperatura ($dT$), el valor de la entropía ($S$) y el volumen ($V$) en la fase 1
$dG = -S_1dT+V_1dp$
y la entropía ($S$) y el volumen ($V$) en la fase 2
$dG = -S_2dT+V_2dp$
resultan en
$\displaystyle\frac{dp}{dT}=\displaystyle\frac{S_2-S_1}{V_2-V_1}$
El cambio en la entropía ($S$) entre ambas fases corresponde a el calor latente ($L$) dividido por la temperatura absoluta ($T$):
$S_2 - S_1 =\displaystyle\frac{ L }{ T }$
Entonces, con la definici n de la variación de volumen en cambio de fase ($\Delta V$)
$\Delta V \equiv V_2 - V_1$
obtenemos la ecuaci n de Clausius-Clapeyron [1,2,3]
| $\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ L }{ \Delta V T }$ |
[1] " ber die Art der Bewegung, welche wir W rme nennen" (Sobre el tipo de movimiento que llamamos calor), Rudolf Clausius, Annalen der Physik und Chemie, 155(6), 368-397. (1850)
[2] "Ueber eine ver nderte Form des zweiten Hauptsatzes der mechanischen W rmetheorie" (Sobre una forma modificada de la segunda ley de la teor a mec nica del calor), Rudolf Clausius, Annalen der Physik, 176(3), 353-400. (1857)
[3] "M moire sur la puissance motrice de la chaleur" (Memoria sobre el poder motriz del calor), Beno t Paul mile Clapeyron, Journal de l' cole Royale Polytechnique, 14, 153-190. (1834)
(ID 15765)
Con la ley de Clausius-Clapeyron, que depende de la variación de la presión ($dp$), la variación de la temperatura ($dT$), el calor latente ($L$), la variación de volumen en cambio de fase ($\Delta V$) y la temperatura absoluta ($T$) y se expresa como:
| $\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ L }{ \Delta V T }$ |
y la definici n de el calor latente molar ($l_m$), en la que el calor latente ($L$) est relacionado con la masa molar ($M_m$) de la siguiente manera:
| $ l_m \equiv\displaystyle\frac{ L }{ M_m }$ |
y el variación del volumen molar en cambio de fase ($\Delta v_m$), en la que la variación de volumen en cambio de fase ($\Delta V$) est relacionado con la masa molar ($M_m$) de la siguiente manera:
| $\Delta v_m =\displaystyle\frac{ \Delta V }{ M_m }$ |
se obtiene:
| $\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ l_m }{ \Delta v_m T }$ |
(ID 15766)
Uno de los fen menos que tambi n incluye la termodin mica es el estudio de los cambios de estado. Existen tres estados b sicos, el gaseoso, el liquido y el solido.
En el caso del gas las part culas se mueven en forma casi libres e interact an solo por choques espor dicos.
En el caso de un liquido la interacci n es permanente. Pese a ello las part culas se logran desplazar sin existir uniones permanentes hacia los vecinos.
En el caso del solido las interacciones son tales que las part culas ya no se logran desplazar y solo oscilan en torno a un punto de equilibrio definido por las part culas vecinas.
El estudio de los cambios de estado trata de explicar porque el material pasa e una forma a la otra y viceversa. En el caso de la medicina dichos cambios son relevantes en procesos en que por ejemplo se evaporan o disuelven sustancias. Esto tanto para la remoci n de materiales como para la reducci n de temperatura como es la transpiraci n.
(ID 147)
El agua es un caso especial ya que su diagrama de fase presenta una diferencia clave con respecto de la gran mayor a de materiales: la linea que separa las fases de solido y liquido tiene pendiente negativa.
Esto se debe a que el agua al pasar de solido a liquido reduce su volumen y con ello la variaci n de volumen $\Delta V$ resulta negativa y la pendiente en la ecuaci n de Clausius Clapeyron termina siendo negativa.
Esta propiedad del agua lleva a que si se le baja la temperatura cuando esta en estado liquido $(dT,negativo)$ al llegar al cambio de fase la presi n se incrementa $(dp)$ mientras que en un liquido normal esta se reduce. Esto es lo que lleva a que en invierno por ejemplo
al congelarse el agua acumulada en las rendijas y grietas de rocas en las monta as genera presi n lo que lleva a su ruptura y finalmente a la erosi n de nuestra geograf a.
al congelarse la superficie de un lago encapsula el agua del lago evitando que esta se pueda expandir para pasar a formar hielo. Esto evita que los lagos se congelen hasta el fondo preservando la vida en su interior.
(ID 146)
Rudolf Clausius (1822-1888) fue un f sico y matem tico alem n que realiz contribuciones significativas en el campo de la termodin mica. Es conocido principalmente por formular la segunda ley de la termodin mica e introducir el concepto de entrop a como una cantidad fundamental en el estudio de la transferencia y transformaci n de energ a en sistemas f sicos.
(ID 1885)
(ID 15345)
ID:(316, 0)