Usuario: 
Calor latente
Storyboard 
El calor latente es la cantidad de calor necesaria para que un material cambie de fase, es decir, pase de estado sólido a líquido, de líquido a gas o de sólido a gas. Se determina llevando a cabo el cambio de fase y midiendo tanto la energía requerida como la cantidad de material que experimenta dicho cambio.
En términos microscópicos, el calor latente corresponde a la energía necesaria para liberar una partícula (átomo o molécula) de un cristal, permitiendo que pase a formar parte de la fase líquida o gaseosa. De manera similar, en el caso de un líquido, es el calor necesario para que una partícula logre escapar de su superficie y se convierta en vapor.
ID:(661, 0)
Calor latente
Imagen
El principio de la medición del calor latente implica llevar a cabo el cambio de fase y medir la energía requerida, como se ilustra en la siguiente imagen:
De esta manera, es posible estimar la energía necesaria para evaporar una cantidad determinada de masa, lo que se traduce en la medición del calor latente, expresado en J/kg o J/mol.
ID:(13543, 0)
Medición de calor de evaporación
Imagen
La medición del calor de evaporación se realiza calentando una muestra, lo que provoca su evaporación, mientras se registra la cantidad de calor suministrada a la muestra. Luego, se enfría el vapor generado y se lo hace condensar, midiendo la masa originalmente evaporada.
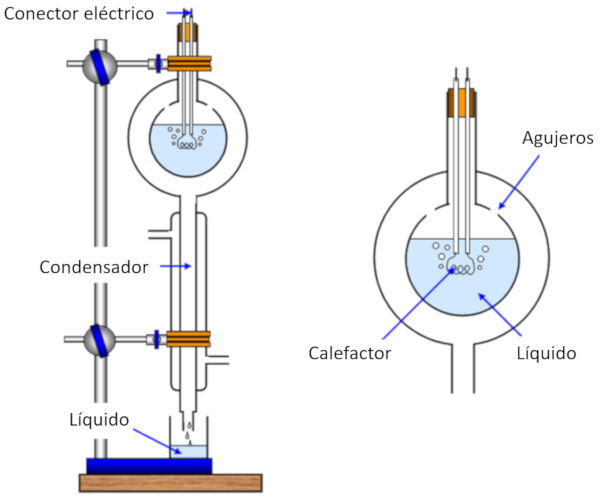
De esta manera, podemos calcular la energía necesaria para evaporar una masa determinada, lo que se expresa como calor latente (L) y se mide en julios por kilogramo (J/kg) o julios por mol (J/mol).
ID:(1662, 0)
Medición de calor de fusión
Imagen
La medición del calor de evaporación se lleva a cabo calentando una muestra, lo que la hace evaporarse, mientras al mismo tiempo se mide el calor suministrado a la muestra. Luego, el vapor se enfría y se condensa, y se mide la masa que originalmente se evaporó.
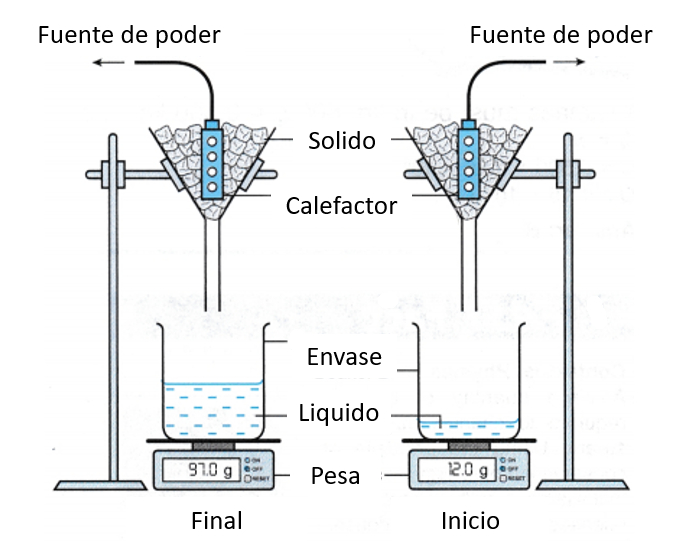
Este proceso permite estimar la energía necesaria para evaporar una cantidad dada de masa, lo que corresponde al calor latente medido en J/kg o J/mol.
ID:(13541, 0)
Modelo
Top
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
\Delta Q = L \Delta m
DQ = L * Dm
\Delta Q = T dS
dQ = T * dS
l_m \equiv\displaystyle\frac{ L }{ M_m }
l_m = L / M_m
m \equiv \displaystyle\frac{ \Delta m }{ N }
m = M / N
m =\displaystyle\frac{ M_m }{ N_A }
m = M_m / N_A
n = \displaystyle\frac{ \Delta m }{ M_m }
n = M / M_m
n \equiv\displaystyle\frac{ N }{ N_A }
n = N / N_A
ID:(15346, 0)
Calor latente específico
Ecuación
La masa evaporada (\Delta m) se define utilizando el calor latente (L) y el calor de cambio de fase (\Delta Q) de la siguiente manera:
| \Delta Q = L \Delta m |
ID:(3200, 0)
Segunda ley de la termodinámica
Ecuación
El diferencial inexacto del calor (\delta Q) es igual a la temperatura absoluta (T) por la variación de la entropía (dS):
| \Delta Q = T dS |
| \delta Q = T dS |
ID:(9639, 0)
Conversión calor latente molar
Ecuación
En muchas ocasiones, no se dispone del calor latente molar, sino del calor latente que se expresa, por ejemplo, en Joules por kilogramo (J/kg). Dado que la ecuación de presión de vapor trabaja con el calor latente molar, es necesario convertir el calor latente en calor latente molar. Como este último se refiere a la cantidad por mol, simplemente dividimos el calor latente (L) por la masa molar (M_m) para obtener el calor latente molar (l_m):
| l_m \equiv\displaystyle\frac{ L }{ M_m } |
En el caso del agua, el calor latente de evaporación es del orden de L\sim 2.256\times 10^6 J/kg, mientras que la masa molar es M_m\sim 18 g/cm^3 = 0.018 kg/m^3. De esta manera, obtenemos un calor latente molar de L_m\sim 40600 J/mol = 40.6 kJ/mol.
ID:(9273, 0)
Masa de la partícula
Ecuación
Si divide la masa (M) por el número de partículas (N) se obtiene la masa de la partícula (m):
| m \equiv \displaystyle\frac{ \Delta m }{ N } |
| m \equiv \displaystyle\frac{ M }{ N } |
ID:(12829, 0)
Masa de la partícula y masa molar
Ecuación
La masa de la partícula (m) puede estimarse a partir de la masa molar (M_m) y el número de Avogadro (N_A) mediante
| m =\displaystyle\frac{ M_m }{ N_A } |
ID:(4389, 0)
Número de moles
Ecuación
El número de moles (n) corresponde a el número de partículas (N) dividido por el número de Avogadro (N_A):
| n \equiv\displaystyle\frac{ N }{ N_A } |
ID:(3748, 0)
Número de moles con masa molar
Ecuación
El número de moles (n) se determina dividiendo la masa (M) de una sustancia por su la masa molar (M_m), que corresponde al peso de un mol de la sustancia.
Por lo tanto, se puede establecer la siguiente relación:
| n = \displaystyle\frac{ \Delta m }{ M_m } |
| n = \displaystyle\frac{ M }{ M_m } |
El número de moles (n) corresponde a el número de partículas (N) dividido por el número de Avogadro (N_A):
| n \equiv\displaystyle\frac{ N }{ N_A } |
Si multiplicamos el numerador y el denominador por la masa de la partícula (m), obtenemos:
n=\displaystyle\frac{N}{N_A}=\displaystyle\frac{Nm}{N_Am}=\displaystyle\frac{M}{M_m}
Así que es:
| n = \displaystyle\frac{ M }{ M_m } |
La masa molar se expresa en gramos por mol (g/mol).
ID:(4854, 0)