Utilizador:
Diagrama de fase da água
Conceito 
Um dos diagramas de fase mais relevantes para o nosso planeta é o da água. Este diagrama apresenta as três fases clássicas: sólida, líquida e gasosa, além de várias fases com diferentes estruturas cristalinas do gelo.
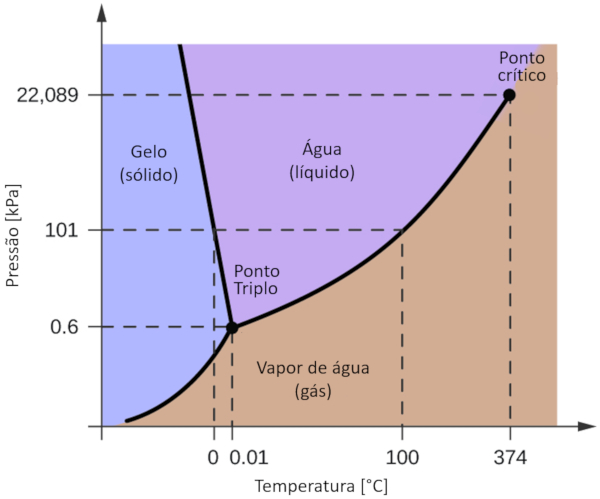
A diferença significativa em relação a outros materiais é que, dentro de uma faixa de pressão que varia de 611 Pa a 209,9 MPa, o estado sólido ocupa um volume maior do que o estado líquido. Essa característica é refletida no diagrama de fase como uma inclinação negativa ao longo da linha de separação entre o estado sólido (gelo hexagonal) e o estado líquido (água).
Esse fenômeno pode ser explicado pela equação de Clausius-Clapeyron:
Neste caso, mostra uma variação negativa no volume:
$\Delta v=v_{água}-v_{gelo}= 18,015,ml/mol-19,645,ml/mol=-1,63,ml/mol<0$
Essa propriedade leva a situações em que, devido à falta de espaço para expansão, a água não congela, preservando a vida contida nela. Por outro lado, a pressão gerada pelo fato de o gelo ocupar mais volume é um dos principais mecanismos de erosão na Terra.
ID:(836, 0)
Lei de Clausius Clapeyron
Conceito
Se o diferencial de energia livre de Gibbs ($dG$) é constante, isso significa que para la variação de pressão ($dp$) e la variação de temperatura ($dT$), os valores de la entropia ($S$) e o volume ($V$) na fase 1
$dG = -S_1dT+V_1dp$
e la entropia ($S$) e o volume ($V$) na fase 2
$dG = -S_2dT+V_2dp$
resultam em
$\displaystyle\frac{dp}{dT}=\displaystyle\frac{S_2-S_1}{V_2-V_1}$
A mudança em la entropia ($S$) entre ambas as fases corresponde a o calor latente ($L$) dividido por la temperatura absoluta ($T$):
$S_2 - S_1 =\displaystyle\frac{ L }{ T }$
Então, com a definição de la variação de volume na mudança de fase ($\Delta V$)
$\Delta V \equiv V_2 - V_1$
obtemos a equação de Clausius-Clapeyron [1,2,3]
| $\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ L }{ \Delta V T }$ |
[1] "Über die Art der Bewegung, welche wir Wärme nennen" (Sobre o Tipo de Movimento que Chamamos Calor), Rudolf Clausius, Annalen der Physik und Chemie, 155(6), 368-397. (1850)
[2] "Ueber eine veränderte Form des zweiten Hauptsatzes der mechanischen Wärmetheorie" (Sobre uma Forma Modificada da Segunda Lei da Teoria Mecânica do Calor), Rudolf Clausius, Annalen der Physik, 176(3), 353-400. (1857)
[3] "Mémoire sur la puissance motrice de la chaleur" (Memória sobre o Poder Motriz do Calor), Benoît Paul Émile Clapeyron, Journal de l'École Royale Polytechnique, 14, 153-190. (1834)
ID:(15765, 0)
Lei molar de Clausius Clapeyron
Conceito
Com a lei de Clausius-Clapeyron, que depende de la variação de pressão ($dp$), la variação de temperatura ($dT$), o calor latente ($L$), la variação de volume na mudança de fase ($\Delta V$) e la temperatura absoluta ($T$), expressa como:
| $\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ L }{ \Delta V T }$ |
e a definição de o calor latente molar ($l_m$), onde o calor latente ($L$) está relacionado a la massa molar ($M_m$) da seguinte forma:
| $ l_m \equiv\displaystyle\frac{ L }{ M_m }$ |
e o variação do volume molar durante a mudança de fase ($\Delta v_m$), onde la variação de volume na mudança de fase ($\Delta V$) está relacionado a la massa molar ($M_m$) da seguinte forma:
| $\Delta v_m =\displaystyle\frac{ \Delta V }{ M_m }$ |
obtemos:
| $\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ l_m }{ \Delta v_m T }$ |
ID:(15766, 0)
Rudolf Clausius
Imagem
Rudolf Clausius (1822-1888) foi um físico e matemático alemão que fez contribuições significativas no campo da termodinâmica. Ele é mais conhecido por formular o segundo princípio da termodinâmica e por introduzir o conceito de entropia como uma quantidade fundamental no estudo da transferência e transformação de energia em sistemas físicos.
ID:(1885, 0)
Modelo
Top
Parâmetros
Variáveis
Cálculos
para 
, depois, selecione a variável: 
para 
Cálculos
Cálculos
Variáve 
Dado Calcular 
Objetivo : Equação A ser usado 
Equações
$\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ L }{ \Delta V T }$
dp / dT = L /( DV * T )
$\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ l_m }{ \Delta v_m T }$
dp / dT = l_m /( Dv_m * T )
$ \Delta Q = L \Delta m$
DQ = L * Dm
$\Delta v_m =\displaystyle\frac{ \Delta V }{ M_m }$
Dv_m = DV / M_m
$ l_m \equiv\displaystyle\frac{ L }{ M_m }$
l_m = L / M_m
ID:(15345, 0)
Calor latente específico
Equação
La massa evaporada ($\Delta m$) é definido usando o calor latente ($L$) e o calor de mudança de fase ($\Delta Q$) da seguinte maneira:
| $ \Delta Q = L \Delta m$ |
ID:(3200, 0)
Lei de Clausius Clapeyron
Equação
A lei Clausius-Clapeyron estabelece uma relação entre la variação de pressão ($dp$) e la variação de temperatura ($dT$) com o calor latente ($L$), la temperatura absoluta ($T$) e ($$)5239 < /var> da seguinte maneira:
| $\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ L }{ \Delta V T }$ |
Se o diferencial de energia livre de Gibbs ($dG$) é constante, significa que, para la variação de pressão ($dp$) e la variação de temperatura ($dT$), os valores de la entropia ($S$) e o volume ($V$) na fase 1
$dG = -S_1dT+V_1dp$
e la entropia ($S$) e o volume ($V$) na fase 2
$dG = -S_2dT+V_2dp$
resultam em
$\displaystyle\frac{dp}{dT}=\displaystyle\frac{S_2-S_1}{V_2-V_1}$
A mudança em la entropia ($S$) entre ambas as fases corresponde a o calor latente ($L$) dividido por la temperatura absoluta ($T$):
$S_2 - S_1 =\displaystyle\frac{ L }{ T }$
Assim, com a definição de la variação de volume na mudança de fase ($\Delta V$)
$\Delta V \equiv V_2 - V_1$
obtemos
| $\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ L }{ \Delta V T }$ |
ID:(12824, 0)
Volume molar
Equação
A variação de volume entre o material em dois estados diferentes pode ser expressa em mols
| $\Delta v_m =\displaystyle\frac{ \Delta V }{ M_m }$ |
para obter um indicador característico do material.
ID:(12823, 0)
Lei molar de Clausius Clapeyron
Equação
A equação de Clausius-Clapeyron estabelece uma relação entre la variação de pressão ($dp$) e la variação de temperatura ($dT$) com la temperatura absoluta ($T$), o calor latente molar ($l_m$) e ($$)9868 < /var> da seguinte maneira:
| $\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ l_m }{ \Delta v_m T }$ |
Com a lei de Clausius-Clapeyron, que depende de la variação de pressão ($dp$), la variação de temperatura ($dT$), o calor latente ($L$), la variação de volume na mudança de fase ($\Delta V$) e la temperatura absoluta ($T$), expressa como:
| $\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ L }{ \Delta V T }$ |
e a definição de o calor latente molar ($l_m$), onde o calor latente ($L$) está relacionado a la massa molar ($M_m$) da seguinte forma:
| $ l_m \equiv\displaystyle\frac{ L }{ M_m }$ |
e o variação do volume molar durante a mudança de fase ($\Delta v_m$), onde la variação de volume na mudança de fase ($\Delta V$) está relacionado a la massa molar ($M_m$) da seguinte forma:
| $\Delta v_m =\displaystyle\frac{ \Delta V }{ M_m }$ |
obtemos:
| $\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ l_m }{ \Delta v_m T }$ |
ID:(12822, 0)