Storyboard

>Modèle

ID:(316, 0)

Iframe

>Top

ID:(15286, 0)

Concept

>Top

L'un des diagrammes de phase les plus pertinents pour notre planète est celui de l'eau. Ce diagramme présente les trois phases classiques : solide, liquide et gazeuse, ainsi que plusieurs phases avec différentes structures cristallines de la glace.

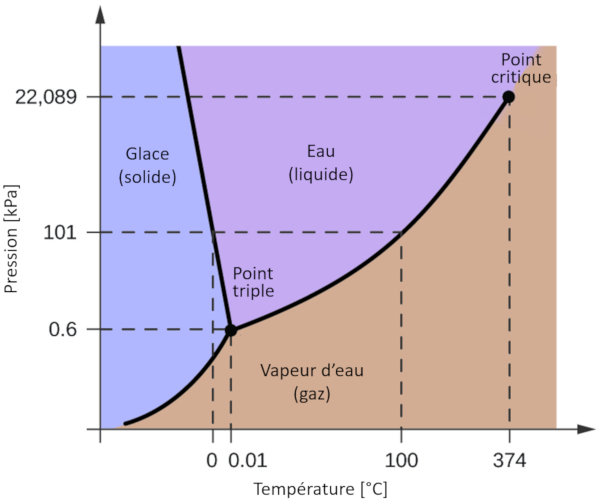
La caractéristique la plus notable par rapport à d'autres matériaux est que, dans une plage de pression allant de 611 Pa à 209,9 MPa, la phase solide occupe un volume plus important que la phase liquide. Cette particularité se reflète dans le diagramme de phase sous la forme d'une pente négative le long de la ligne de séparation entre la phase solide (glace hexagonale) et la phase liquide (eau).

ID:(836, 0)

Concept

>Top

Si le différentiel d'énergie libre de Gibbs ($dG$) est constant, cela signifie que pour a variation de pression ($dp$) et a variation de température ($dT$), les valeurs de a entropie ($S$) et le volume ($V$) dans la phase 1

$dG = -S_1dT+V_1dp$

et a entropie ($S$) et le volume ($V$) dans la phase 2

$dG = -S_2dT+V_2dp$

résultent en

$\displaystyle\frac{dp}{dT}=\displaystyle\frac{S_2-S_1}{V_2-V_1}$

Le changement de a entropie ($S$) entre les deux phases correspond à Le chaleur latente ($L$) divisé par a température absolue ($T$):

$S_2 - S_1 =\displaystyle\frac{ L }{ T }$

Puis, avec la définition de a variation de volume en changement de phase ($\Delta V$)

$\Delta V \equiv V_2 - V_1$

nous obtenons l'équation de Clausius-Clapeyron [1,2,3]

[1] "Über die Art der Bewegung, welche wir Wärme nennen" (Sur la nature du mouvement que nous appelons chaleur), Rudolf Clausius, Annalen der Physik und Chemie, 155(6), 368-397. (1850)

[2] "Ueber eine veränderte Form des zweiten Hauptsatzes der mechanischen Wärmetheorie" (Sur une forme modifiée de la seconde loi de la théorie mécanique de la chaleur), Rudolf Clausius, Annalen der Physik, 176(3), 353-400. (1857)

[3] "Mémoire sur la puissance motrice de la chaleur", Benoît Paul Émile Clapeyron, Journal de l'École Royale Polytechnique, 14, 153-190. (1834)

ID:(15765, 0)

Concept

>Top

Avec la loi de Clausius-Clapeyron, qui dépend de a variation de pression ($dp$), a variation de température ($dT$), le chaleur latente ($L$), a variation de volume en changement de phase ($\Delta V$) et a température absolue ($T$), exprimée comme suit :

et la définition de le chaleur latente molaire ($l_m$), où Le chaleur latente ($L$) est lié à A masse molaire ($M_m$) comme suit :

et le variation du volume molaire lors du changement de phase ($\Delta v_m$), où A variation de volume en changement de phase ($\Delta V$) est lié à A masse molaire ($M_m$) comme suit :

nous obtenons :

ID:(15766, 0)

Image

>Top

Rudolf Clausius (1822-1888) était un physicien et mathématicien allemand qui a apporté d'importantes contributions dans le domaine de la thermodynamique. Il est surtout connu pour avoir formulé le deuxième principe de la thermodynamique et pour avoir introduit le concept d'entropie en tant que quantité fondamentale dans l'étude des transferts et des transformations d'énergie dans les systèmes physiques.

ID:(1885, 0)

Top

>Top

Paramètres

$L$

L

Chaleur latente

J/kg

$l_m$

l_m

Chaleur latente molaire

J/mol

$\Delta m$

Dm

Masse évaporée

kg

$M_m$

M_m

Masse molaire

kg/mol

$dp$

dp

Variation de pression

Pa

$\Delta V$

DV

Variation de volume en changement de phase

m^3

$\Delta v_m$

Dv_m

Variation du volume molaire lors du changement de phase

m^3/mol

Variables

$\Delta Q$

DQ

Chaleur fournie au liquide ou au solide

J

$T$

T

Température absolue

K

$dT$

dT

Variation de température

K

Calculs

• Méthode alternative
• Méthode traditionnelle
• Stratégie
• 2D
• 3D

Équation

Nombre

D'abord, sélectionnez l'équation: à , puis, sélectionnez la variable: à

---

Calculs

Symbole

Équation

Résolu

Traduit

Calculs

Symbole

Équation

Résolu

Traduit

Variable Donnée Calculer Cible : Équation À utiliser

Équations

ID:(15345, 0)

Équation

>Top, >Modèle

A masse évaporée ($\Delta m$) est défini en utilisant le chaleur latente ($L$) et le chaleur à changement de phase ($\Delta Q$) de la manière suivante :

$\Delta Q = L \Delta m$

Conditions

Variables

$\Delta Q$

Chaleur fournie au liquide ou au solide

$J$

10151

$L$

Chaleur latente

$J/kg$

5238

$\Delta m$

Masse évaporée

$kg$

5248

Relation

ID:(3200, 0)

Équation

>Top, >Modèle

La loi Clausius-Clapeyron établit une relation entre a variation de pression ($dp$) et a variation de température ($dT$) avec le chaleur latente ($L$), a température absolue ($T$) et ($$)5239 < /var> comme suit :

$\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ L }{ \Delta V T }$

Conditions

Variables

$L$

Chaleur latente

$J/kg$

5238

$T$

Température absolue

$K$

5177

$dp$

Variation de pression

$Pa$

5240

$dT$

Variation de température

$K$

5217

$\Delta V$

Variation de volume en changement de phase

$m^3$

5239

Relation

Développement

Si le différentiel d'énergie libre de Gibbs ($dG$) est constant, cela signifie que pour a variation de pression ($dp$) et a variation de température ($dT$), les valeurs de a entropie ($S$) et le volume ($V$) en phase 1

$dG = -S_1dT+V_1dp$

et a entropie ($S$) et le volume ($V$) en phase 2

$dG = -S_2dT+V_2dp$

donnent

$\displaystyle\frac{dp}{dT}=\displaystyle\frac{S_2-S_1}{V_2-V_1}$

La variation de a entropie ($S$) entre les deux phases correspond à Le chaleur latente ($L$) divisé par a température absolue ($T$) :

$S_2 - S_1 =\displaystyle\frac{ L }{ T }$

Ainsi, avec la définition de a variation de volume en changement de phase ($\Delta V$)

$\Delta V \equiv V_2 - V_1$

nous obtenons

$\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ L }{ \Delta V T }$

ID:(12824, 0)

Équation

>Top, >Modèle

ID:(9273, 0)

Équation

>Top, >Modèle

La variation de volume entre le matériau à deux états différents peut être exprimée en moles

$\Delta v_m =\displaystyle\frac{ \Delta V }{ M_m }$

Conditions

Variables

$M_m$

Masse molaire

$kg/mol$

6212

$\Delta V$

Variation de volume en changement de phase

$m^3$

5239

$\Delta v_m$

Variation du volume molaire lors du changement de phase

$m^3/mol$

9868

Relation

pour obtenir un indicateur caractéristique du matériau.

ID:(12823, 0)

Équation

>Top, >Modèle

L'équation de Clausius-Clapeyron établit une relation entre a variation de pression ($dp$) et a variation de température ($dT$) avec a température absolue ($T$), le chaleur latente molaire ($l_m$) et ($$)9868 < /var> comme suit :

$\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ l_m }{ \Delta v_m T }$

Conditions

Variables

$l_m$

Chaleur latente molaire

$J/mol$

9867

$T$

Température absolue

$K$

5177

$dp$

Variation de pression

$Pa$

5240

$dT$

Variation de température

$K$

5217

$\Delta v_m$

Variation du volume molaire lors du changement de phase

$m^3/mol$

9868

Relation

Développement

Avec la loi de Clausius-Clapeyron, qui dépend de a variation de pression ($dp$), a variation de température ($dT$), le chaleur latente ($L$), a variation de volume en changement de phase ($\Delta V$) et a température absolue ($T$), exprimée comme suit :

$\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ L }{ \Delta V T }$

et la définition de le chaleur latente molaire ($l_m$), où Le chaleur latente ($L$) est lié à A masse molaire ($M_m$) comme suit :

$l_m \equiv\displaystyle\frac{ L }{ M_m }$

et le variation du volume molaire lors du changement de phase ($\Delta v_m$), où A variation de volume en changement de phase ($\Delta V$) est lié à A masse molaire ($M_m$) comme suit :

$\Delta v_m =\displaystyle\frac{ \Delta V }{ M_m }$

nous obtenons :

$\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ l_m }{ \Delta v_m T }$

ID:(12822, 0)