Storyboard

>Modelo

ID:(600, 0)

Equação

>Top, >Modelo

Uma aplicação simples do teorema de Steiner é uma massa pontual $m$ a uma distância $L$ de um eixo. Como uma massa pontual não possui dimensões, ela não possui momento de inércia em relação ao seu centro de massa. No entanto, como o centro de massa está a uma distância de $L$ do eixo, de acordo com o teorema de Steiner,

o seu momento de inércia será

$I = m L ^2$

Condições

Variáveis

$L$

Comprimento do pêndulo

$m$

6282

$I$

Momento de inércia de um pêndulo matemático

$kg m^2$

9799

$m$

Ponto de massa

$kg$

6281

Relação

.

ID:(9880, 0)

Equação

>Top, >Modelo

O momento de inércia total $I_t$ de um objeto é calculado somando os momentos de inércia de suas partes que são comparáveis ao momento de inércia de uma partícula individual,

resultando em um momento de inércia como

$I_t=\sum_kI_k$

Condições

Variáveis

$I_k$

Momento de Inércia do k-ésimo Elemento

$kg m^2$

6160

$I_t$

Momento Total de Inércia

$kg m^2$

6161

Relação

.

ID:(4438, 0)

Imagem

>Top

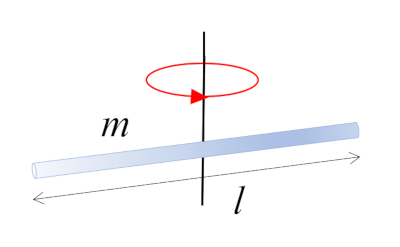
Uma barra com massa $m$ e comprimento $l$ que gira em torno do seu centro, que coincide com o centro de massa:

ID:(10962, 0)

Equação

>Top, >Modelo

O momento de inércia de uma barra que está em rotação em torno de um eixo perpendicular ($\perp$) que passa pelo centro é obtido ao dividir o corpo em pequenos volumes e somá-los:



resultando em

$I_{CM} =\displaystyle\frac{1}{12} m l ^2$

Condições

Variáveis

$l$

Comprimento da barra fina

$m$

6151

$m$

Massa corporal

$kg$

6150

$I_{CM}$

Momento de inércia CM de uma barra fina, eixo perpendicular

$kg m^2$

5323

Relação

.

ID:(4432, 0)

Imagem

>Top

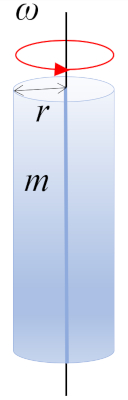
Uma rotação de um cilindro com massa $m$ e raio $r$ em torno do eixo do cilindro, onde o centro de massa (CM) está localizado a meia altura:

ID:(10964, 0)

Equação

>Top, >Modelo

O momento de inércia de um cilindro que está em rotação em torno de um eixo paralelo ($\parallel$) que passa pelo centro é obtido ao dividir o corpo em pequenos volumes e somá-los:



resultando em

$I_{CM} =\displaystyle\frac{1}{2} m r_c ^2$

Condições

Variáveis

$m$

Massa corporal

$kg$

6150

$I_{CM}$

Momento de inércia CM de um cilindro, eixo paralelo ao eixo do cilindro

$kg m^2$

5324

$r_c$

Raio do cilindro

$m$

5319

Relação

.

ID:(4434, 0)

Imagem

>Top

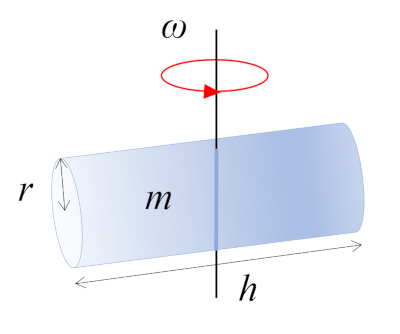
Neste cenário, um cilindro com massa $m$, raio $r$ e altura $h$ está girando em torno de um eixo perpendicular ao seu próprio eixo. Esse eixo passa pelo ponto médio do comprimento do cilindro, onde se encontra o centro de massa (CM):

ID:(10965, 0)

Equação

>Top, >Modelo

O momento de inércia de um cilindro que está em rotação em torno de um eixo perpendicular ($\perp$) que passa pelo centro é obtido ao dividir o corpo em pequenos volumes e somá-los:



resultando em

$I_{CM} =\displaystyle\frac{1}{12} m ( h ^2+3 r_c ^2)$

Condições

Variáveis

$h$

Altura do cilindro

$m$

5318

$m$

Massa corporal

$kg$

6150

$r_c$

Raio do cilindro

$m$

5319

Relação

.

ID:(4435, 0)

Imagem

>Top

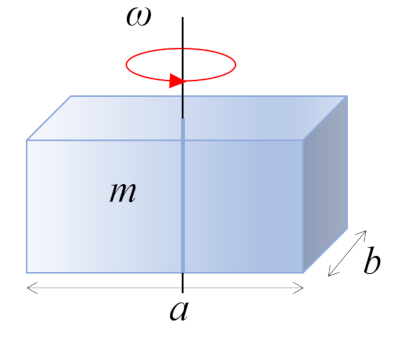
Um paralelepípedo reto com massa $m$ e lados $a$ e $b$, perpendicular ao eixo de rotação, está girando em torno de seu centro de massa, que se encontra no centro geométrico do corpo:

ID:(10973, 0)

Equação

>Top, >Modelo

O momento de inércia de um paralelepípedo que está em rotação em torno de um eixo que passa pelo centro é obtido ao dividir o corpo em pequenos volumes e somá-los:



resultando em

$I_{CM} =\displaystyle\frac{1}{12} m ( a ^2+ b ^2)$

Condições

Variáveis

$a$

Comprimento da aresta de um paralelepípedo reto

$m$

6152

$b$

Largura da aresta de um paralelepípedo reto

$m$

6153

$m$

Massa corporal

$kg$

6150

$I_{CM}$

Momento de Inércia CM de um Paralelepípedo, Eixo Central da Face

$kg m^2$

5322

Relação

.

ID:(4433, 0)

Imagem

>Top

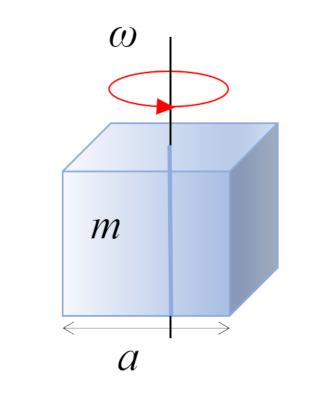
No caso de um paralelepípedo reto com massa $m$ e lado $a$, o centro de massa está localizado no centro geométrico:

ID:(10963, 0)

Equação

>Top, >Modelo

ID:(10972, 0)

Imagem

>Top

Uma esfera com massa $m$ e raio $r$ está girando em torno do seu centro de massa, que se localiza no centro da esfera:

ID:(10490, 0)

Equação

>Top, >Modelo

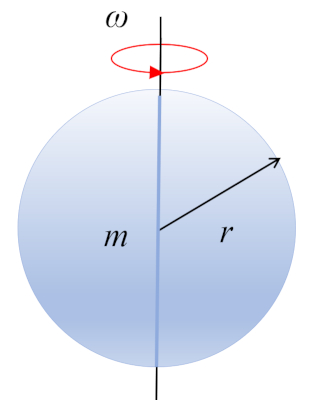
O momento de inércia de uma esfera que gira em torno de um eixo que passa pelo centro é obtido pela segmentação do corpo em pequenos volumes e somando:



resultando em

$I_{CM} =\displaystyle\frac{2}{5} m r_e ^2$

Condições

Variáveis

$m$

Massa corporal

$kg$

6150

$I_{CM}$

Momento de Inércia CM de uma Esfera

$kg m^2$

5326

$r_e$

Raio da esfera

$m$

5321

Relação

.

ID:(4436, 0)

0

Video

Vídeo: Momento de inércia