Utilizador:
Momento de inércia da barra, eixo perpendicular
Storyboard 
O momento de inércia é o equivalente rotacional da massa no movimento de translação. No caso de uma barra que gira em torno de um eixo perpendicular ao seu próprio eixo, o caso mais simples ocorre quando a rotação acontece ao redor do centro de massa.
ID:(2090, 0)
Momento de inércia para um eixo que não passa pelo centro de massa
Descrição
Quando o eixo de rotação não passa pelo centro de massa (CM), o momento de inércia $I$ pode ser calculado usando o Teorema de Steiner. Para isso, começa-se com o momento de inércia em relação ao centro de massa, por exemplo:
• Para uma barra com um eixo perpendicular, é calculado
| $ I_{CM} =\displaystyle\frac{1}{12} m l ^2$ |
• Para um cilindro com um eixo perpendicular, é calculado
| $ I_{CM} =\displaystyle\frac{1}{12} m ( h ^2+3 r_c ^2)$ |
• Para um cilindro com um eixo paralelo, é calculado
| $ I_{CM} =\displaystyle\frac{1}{2} m r_c ^2$ |
• Para um paralelepípedo, é calculado
| $ I_{CM} =\displaystyle\frac{1}{12} m ( a ^2+ b ^2)$ |
• Para um cubo, é calculado
| $ I_{CM} =\displaystyle\frac{1}{6} m a ^2$ |
• Para uma esfera, é calculado
| $ I_{CM} =\displaystyle\frac{2}{5} m r_e ^2$ |
Em seguida, a massa multiplicada pelo quadrado da distância entre o eixo de rotação e o centro de massa é adicionada
| $ I = I_{CM} + m d ^2$ |
ID:(15867, 0)
Barra que gira em torno de um eixo $\perp$
Imagem
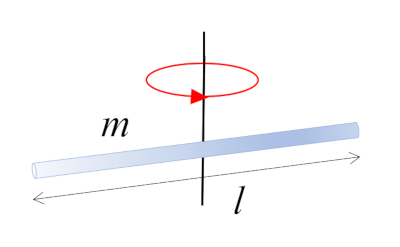
Uma barra com massa $m$ e comprimento $l$ que gira em torno do seu centro, que coincide com o centro de massa:
ID:(10962, 0)
Modelo
Top
Parâmetros
Variáveis
Cálculos
para 
, depois, selecione a variável: 
para 
Cálculos
Cálculos
Variáve 
Dado Calcular 
Objetivo : Equação A ser usado 
Equações
$ I = I_{CM} + m d ^2$
I = I_CM + m * d ^ 2
$ I_{CM} =\displaystyle\frac{1}{12} m l ^2$
I_CM = m * l ^ 2 / 12
$ \omega = \omega_0 + \alpha_0 ( t - t_0 )$
omega = omega_0 + alpha_0 * ( t - t_0 )
$ T = I \alpha_0 $
T = I * alpha
$ T = r F $
T = r * F
$ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$
theta = theta_0 + omega_0 *( t - t_0 )+ alpha_0 *( t - t_0 )^2/2
$ \theta = \theta_0 +\displaystyle\frac{ \omega ^2- \omega_0 ^2}{2 \alpha_0 }$
theta = theta_0 +( omega ^2 - omega_0 ^2)/(2* alpha_0 )
ID:(15859, 0)
Momento de inércia da barra de comprimento $l$ eixo $\perp$
Equação
O momento de inércia de uma barra que está em rotação em torno de um eixo perpendicular ($\perp$) que passa pelo centro é obtido ao dividir o corpo em pequenos volumes e somá-los:
resultando em
| $ I_{CM} =\displaystyle\frac{1}{12} m l ^2$ |
.
ID:(4432, 0)
Teorema de Steiner
Equação
La momento de inércia do eixo que não passa pelo CM ($I$) pode ser calculado usando la momento de inércia do centro de massa ($I_{CM}$) e somando o momento de inércia de la massa corporal ($m$) como se fosse uma massa pontual em la distância centro de massa e eixo ($d$):
| $ I = I_{CM} + m d ^2$ |
ID:(3688, 0)
Torque para momento de inércia constante
Equação
No caso em que o momento de inércia é constante, a derivada do momento angular é igual a
| $ L = I \omega $ |
o que implica que o torque é igual a
| $ T = I \alpha_0 $ |
| $ T = I \alpha $ |
Como o momento é igual a
| $ L = I \omega $ |
segue-se que no caso em que o momento de inércia não muda com o tempo,
$T=\displaystyle\frac{dL}{dt}=\displaystyle\frac{d}{dt}(I\omega) = I\displaystyle\frac{d\omega}{dt} = I\alpha$
o que implica que
| $ T = I \alpha $ |
.
Essa relação é o equivalente da segunda lei de Newton para a rotação em vez da translação.
ID:(3253, 0)
Torque simples - relação de força
Equação
Dado que a relação entre o momento angular e o torque é
| $ L = r p $ |
sua derivada temporal nos leva à relação do torque
| $ T = r F $ |
A rotação do corpo ocorre em torno de um eixo na direção do torque, que passa pelo centro de massa.
ID:(4431, 0)
Velocidade angular com aceleração angular constante
Equação
Com la aceleração angular constante ($\alpha_0$), la velocidade angular ($\omega$) forma uma relação linear com o tempo ($t$), incorporando as variáveis la velocidade angular inicial ($\omega_0$) e o tempo inicial ($t_0$) da seguinte forma:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
Se assumirmos que la aceleração angular média ($\bar{\alpha}$) é constante, equivalente a la aceleração angular constante ($\alpha_0$), então a seguinte equação se aplica:
| $ \bar{\alpha} = \alpha_0 $ |
Portanto, considerando la diferença de velocidades angulares ($\Delta\omega$) junto com la velocidade angular ($\omega$) e la velocidade angular inicial ($\omega_0$):
| $ \Delta\omega = \omega - \omega_0 $ |
e o tempo decorrido ($\Delta t$) em relação a o tempo ($t$) e o tempo inicial ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
a equação para la aceleração angular média ($\bar{\alpha}$):
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
pode ser expressa como:
$\alpha_0 = \alpha = \displaystyle\frac{\Delta \omega}{\Delta t} = \displaystyle\frac{\omega - \omega_0}{t - t_0}$
Resolvendo isso, obtemos:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
Esta equação representa uma linha reta no plano de velocidade angular versus tempo.
ID:(3237, 0)
Ângulo para aceleração angular constante
Equação
Dado que o deslocamento total corresponde à área sob a curva de velocidade angular versus tempo, no caso de uma aceleração angular constante ($\alpha_0$), determina-se que o deslocamento o ângulo ($\theta$) com as variáveis o ângulo inicial ($\theta_0$), o tempo ($t$), o tempo inicial ($t_0$) e la velocidade angular inicial ($\omega_0$) é o seguinte:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
No caso de la aceleração angular constante ($\alpha_0$), la velocidade angular ($\omega$) como função de o tempo ($t$) segue uma relação linear com o tempo inicial ($t_0$) e la velocidade angular inicial ($\omega_0$) na forma:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
Dado que o deslocamento angular é igual à área sob a curva de velocidade angular-tempo, neste caso, pode-se adicionar as contribuições do retângulo:
$\omega_0(t-t_0)$
e do triângulo:
$\displaystyle\frac{1}{2}\alpha_0(t-t_0)^2$
Isso nos leva à expressão para o ângulo ($\theta$) e o ângulo inicial ($\theta_0$):
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
Essa expressão corresponde à forma geral de uma parábola.
ID:(3682, 0)
Ângulo de frenagem em função da velocidade angular
Equação
No caso de la aceleração angular constante ($\alpha_0$), a função de la velocidade angular ($\omega$) em relação a o tempo ($t$), juntamente com as variáveis adicionais la velocidade angular inicial ($\omega_0$) e o tempo inicial ($t_0$), é expressa pela equação:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
A partir desta equação, é possível calcular a relação entre o ângulo ($\theta$) e o ângulo inicial ($\theta_0$), bem como a mudança na velocidade angular:
| $ \theta = \theta_0 +\displaystyle\frac{ \omega ^2- \omega_0 ^2}{2 \alpha_0 }$ |
Se resolvermos o tempo na equação de la velocidade angular ($\omega$) que inclui as variáveis la velocidade angular inicial ($\omega_0$), o tempo ($t$), o tempo inicial ($t_0$) e la aceleração angular constante ($\alpha_0$):
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
obtemos a seguinte expressão para o tempo:
$t - t_0 = \displaystyle\frac{\omega - \omega_0}{\alpha_0}$
Esta solução pode ser substituída na equação para calcular o ângulo ($\theta$) usando o ângulo inicial ($\theta_0$) da seguinte forma:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
o que resulta na seguinte equação:
| $ \theta = \theta_0 +\displaystyle\frac{ \omega ^2- \omega_0 ^2}{2 \alpha_0 }$ |
ID:(4386, 0)