Moment d'inertie d'une particule hors axe
Équation 
Une application simple du théorème de Steiner est une masse ponctuelle m à une distance L d'un axe. Comme une masse ponctuelle n'a pas de dimensions, elle n'a pas de moment d'inertie par rapport à son centre de masse. Cependant, comme le centre de masse est à une distance de L de l'axe selon le théorème de Steiner,
| I = I_{CM} + m d ^2 |
son moment d'inertie sera
.
ID:(9880, 0)
Méthode de calcul du moment d'inertie
Équation 
Le moment d'inertie total I_t d'un objet est calculé en additionnant les moments d'inertie de ses composants qui sont comparables au moment d'inertie d'une particule individuelle,
| I = m r ^2 |
ce qui conduit à un moment d'inertie résultant de
.
ID:(4438, 0)
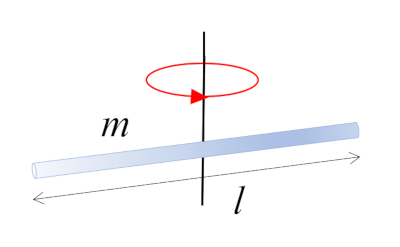
Barre qui tourne autour d'un axe \perp
Image 
Une barre de masse m et de longueur l qui tourne autour de son centre, qui coïncide avec le centre de masse :
ID:(10962, 0)
Moment d'inertie de la barre de longueur l axe \perp
Équation 
Le moment d'inertie d'une barre en rotation autour d'un axe perpendiculaire (\perp) passant par le centre est obtenu en divisant le corps en petits volumes et en les additionnant :
ce qui aboutit à
.
ID:(4432, 0)
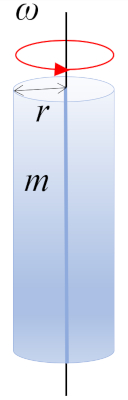
Cylindre qui tourne autour de l'axe \parallel
Image 
Considérons une rotation d'un cylindre de masse m et de rayon r autour de l'axe du cylindre, où le centre de masse (CM) se situe à mi-hauteur :
ID:(10964, 0)
Moment d'inertie du cylindre, axe \parallel
Équation 
Le moment d'inertie d'un cylindre en rotation autour d'un axe parallèle (\parallel) à son axe central est obtenu en segmentant le corps en petits volumes et en les additionnant :
ce qui aboutit à
.
ID:(4434, 0)
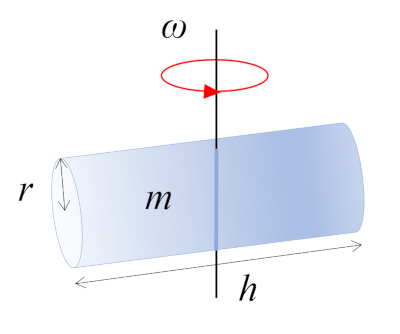
Cylindre qui tourne autour de l'axe \perp
Image 
Dans cette situation, un cylindre avec une masse m, un rayon r et une hauteur h tourne autour d'un axe perpendiculaire à son propre axe. Cet axe passe par le milieu de la longueur du cylindre, où se trouve le centre de masse (CM) :
ID:(10965, 0)
Moment d'inertie du cylindre, axe \perp
Équation 
Le moment d'inertie d'un cylindre en rotation autour d'un axe perpendiculaire (\perp) passant par le centre est obtenu en divisant le corps en petits volumes et en les additionnant :
ce qui aboutit à
.
ID:(4435, 0)
Moment d'inertie d'un parallélépipède régulier
Image 
Un parallélépipède rectangle de masse m et de côtés a et b, perpendiculaire à l'axe de rotation, tourne autour de son centre de masse, qui se trouve au centre géométrique du corps:
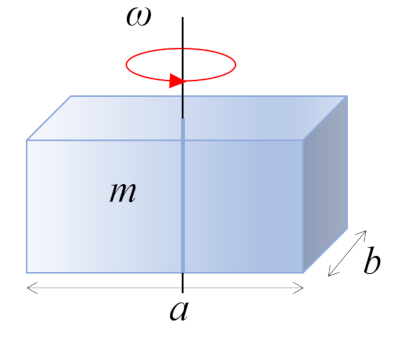
ID:(10973, 0)
Moment d'inertie d'un parallélépipède rectangle
Équation 
Le moment d'inertie d'un parallélépipède en rotation autour d'un axe passant par son centre est obtenu en divisant le corps en petits volumes et en les additionnant :
ce qui aboutit à
.
ID:(4433, 0)
Parallélépipède droit
Image 
Dans le cas d'un parallélépipède rectangle avec une masse m et un côté a, le centre de masse se situe au centre géométrique :
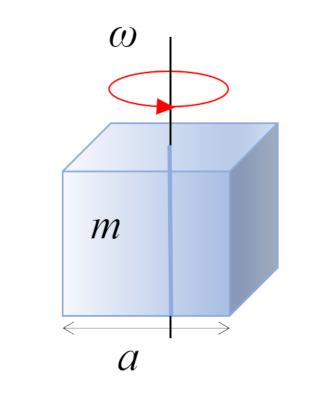
ID:(10963, 0)
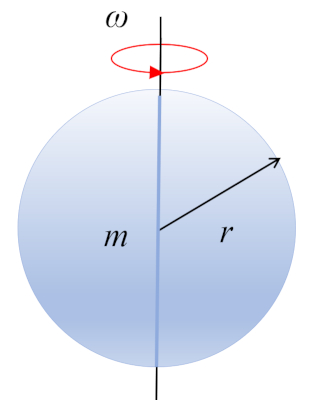
Moment d'inertie d'une sphère
Équation 
Le moment d'inertie d'une sphère en rotation autour d'un axe passant par son centre est obtenu en segmentant le corps en petits volumes et en les additionnant :
ce qui donne comme résultat :
.
ID:(4436, 0)
0
Video
Vidéo: Moment d'inertie