Usuario:
Fuerza de Stokes
Storyboard 
Un ejemplo de fuerza viscosa es el modelo desarrollado cuando una esfera se desplaza en un medio viscoso. Este modelo y la ecuación correspondiente se conocen por el nombre de su autor, George Stokes.
La fuerza de Stokes está condicionada por la viscosidad del medio, el radio de la esfera y la velocidad a la que se mueve en el medio. De manera similar, si el medio se desplaza, arrastra el objeto junto con él.
ID:(1964, 0)
Mecanismos
Iframe
Mecanismos
ID:(15540, 0)
George Stokes
Descripción
George Stokes realizó numerosos trabajos en hidrodinámica y matemáticas, siendo principalmente recordado por la conocida ley de Stokes aplicada a cuerpos esféricos en un flujo y por el teorema de Stokes en matemáticas.
George Gabriel Stokes (1819-1903)
ID:(12535, 0)
Fuerzas sobre una esfera que cae en un medio
Descripción
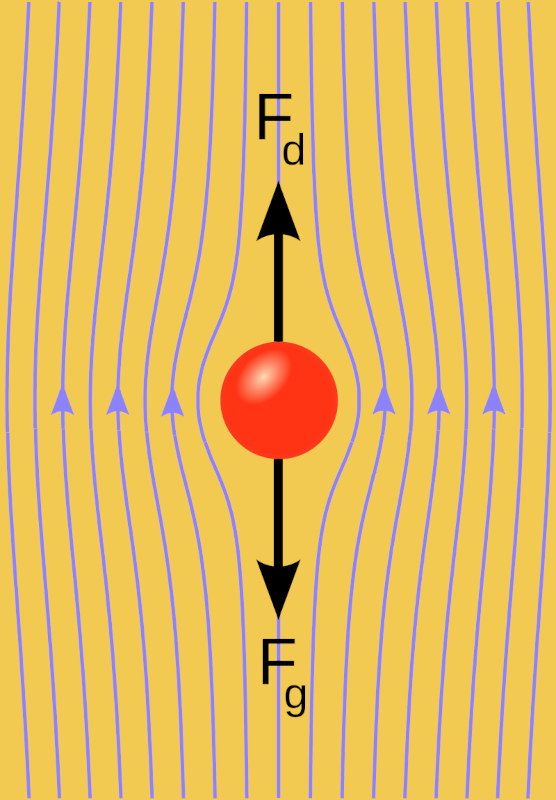
Cuando se arroja una esfera en un medio viscoso, aparece una fuerza ascendente inicial, una fuerza gravitacional ($F_g$), que comienza a hundir progresivamente el cuerpo. Durante este proceso, la esfera gana velocidad, dando lugar a una fuerza descendente, una fuerza viscosa ($F_v$), que depende de la velocidad. A medida que la velocidad total, la fuerza con masa constante ($F$),
| $ F = F_g - F_v $ |
comienza a reducirse hasta volverse nula. A partir de este momento, el movimiento continúa a una velocidad constante, ya que no hay fuerza que lo acelere.
ID:(15544, 0)
Fuerza de Stokes
Top
La fuerza de Stokes es la fuerza generada por el flujo alrededor de una esfera de radio de la gota ($r$) inmersa en él. En este caso, se utiliza el modelo de la fuerza proporcional a la velocidad ($v$):
| $ F_v = b v $ |
En este contexto, se puede demostrar que la constante de fuerza viscosa ($b$) con la viscosidad ($\eta$) es igual a:
| $ b \equiv 6 \pi \eta r $ |
por lo tanto, la fuerza de Stokes se expresa como:
| $ F_v =6 \pi \eta r v $ |
Esta fuerza se aplica principalmente en flujos laminares.
ID:(15555, 0)
Velocidad de caída en medio viscoso
Top
El movimiento de una esfera en dos dimensiones se caracteriza por la componente x de la velocidad ($v_x$) con la velocidad horizontal inicial ($v_{0x}$), la tiempo de adaptación ($\tau$) y el tiempo ($t$):
| $ v_x = v_{0x} e^{- t / \tau }$ |
y la componente y de la velocidad ($v_y$) con la velocidad vertical inicial ($v_{0y}$), la tiempo de adaptación ($\tau$), la aceleración gravitacional ($g$) y el tiempo ($t$):
| $ v_y = g \tau + ( v_{0y} - g \tau )e^{- t / \tau }$ |
que se representa en un diagrama $v_x$ vs $v_y$:
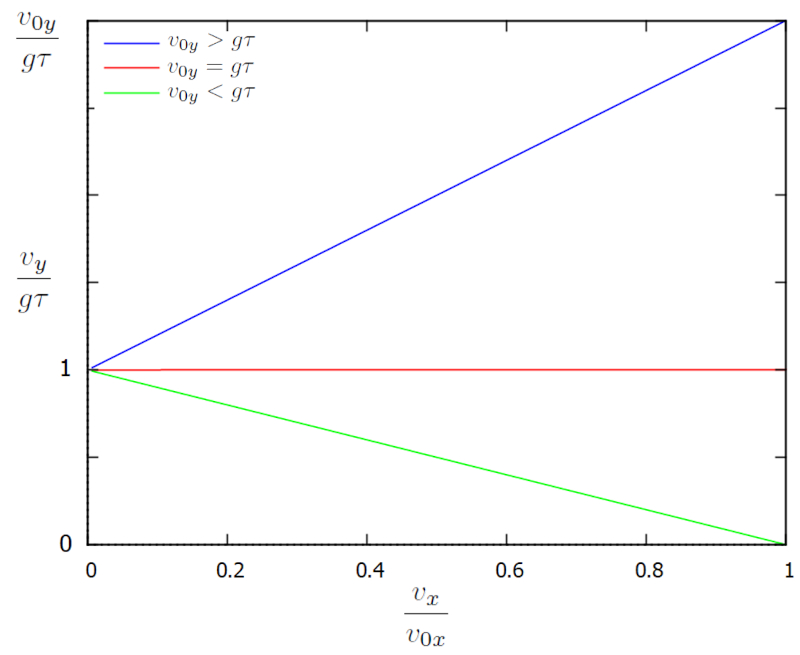
El diagrama muestra cómo ambas componentes de la velocidad evolucionan en el tiempo. Inicialmente, $v$ es igual a $v_{0x}$, lo que corresponde a un punto en el borde derecho del gráfico. Con el tiempo, las componentes de la velocidad evolucionan desde el lado derecho hasta el borde izquierdo, donde la velocidad horizontal es nula y la velocidad vertical llega al límite $g\tau$, por lo que $v/g\tau$ es igual a uno.
ID:(15558, 0)
Camino de caída en medio viscoso
Top
El desplazamiento horizontal se puede calcular mediante la ecuación pour la posición en el eje x ($x$) con la posición inicial en el eje x ($x_0$), la velocidad horizontal inicial ($v_{0x}$), la tiempo de adaptación ($\tau$) y el tiempo ($t$) :
| $ x = x_0 + v_{0x} \tau (1 - e^{- t / \tau })$ |
y el desplazamiento vertical de la posición en el eje y ($y$) con la posición inicial en el eje y ($y_0$), la velocidad horizontal inicial ($v_{0x}$), la tiempo de adaptación ($\tau$) y el tiempo ($t$) :
| $ y = y_0 + \tau g t + \tau ( v_{0y} - g \tau )(1 - e^{- t / \tau })$ |
lo que se grafica en las posiciones $x$ vs $y$ :
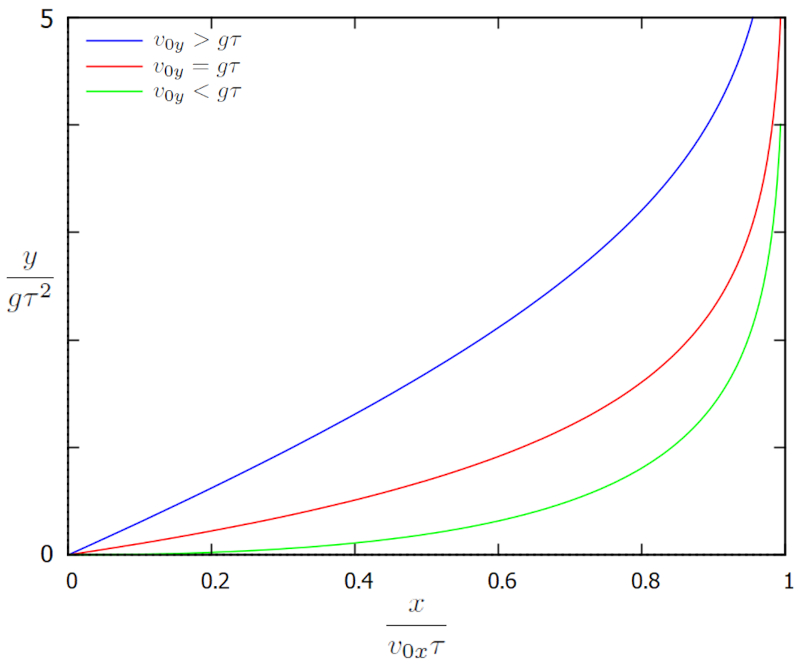
En este caso, la posición evoluciona desde el borde izquierdo hacia el derecho, donde se detiene en su movimiento horizontal alcanzando una distancia máxima de $v_{0x}\tau$. El desplazamiento vertical se describe con un sistema de coordenadas cuyo origen se encuentra en el punto donde comienza la trayectoria y que en su versión vertical apunta hacia abajo. En ese sentido, el incremento en $y$ corresponde al descenso de la esfera en la dirección de la gravedad.
ID:(15559, 0)
Método de Ostwald para medir viscosidad
Descripción
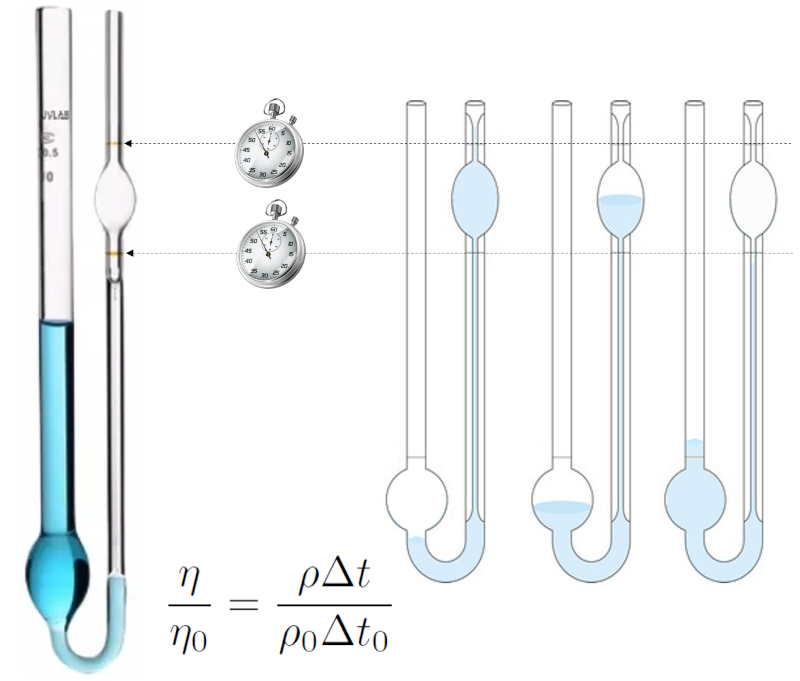
El método de medición de viscosidad de Ostwald se basa en el comportamiento de un líquido que fluye por un tubo de radio pequeño (capilar).
Se introduce el líquido, se succiona para que su nivel sobrepase la marca superior y luego se deja escurrir, midiendo el tiempo que el nivel tarda en pasar del nivel superior al inferior.
El experimento se realiza primero con un líquido para el cual se conoce la viscosidad y densidad (por ejemplo, agua destilada), y luego con el líquido para el cual se busca determinar la viscosidad. Si las condiciones son iguales, el líquido que fluya en ambos casos será similar, y con ello, el tiempo será proporcional a la densidad dividida por la viscosidad. Así, se puede establecer una ecuación de comparación entre ambas viscosidades:
ID:(15545, 0)
Modelo
Top
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
$ b \equiv 6 \pi \eta r $
b = 6* pi * eta * r
$ F = F_g - F_v $
F = F_g - F_v
$ F = m_i a $
F = m_i * a
$ F_g = m_g g $
F_g = m_g * g
$ F_v = b v $
F_v = b * v
$ F_v =6 \pi \eta r v $
F_v =6* pi * eta * r * v
$ m_g = m_i $
m_g = m_i
$ m_i a = m_g g - b v $
m_i * a = m_g * g - b * v
$ \rho \equiv\displaystyle\frac{ m_i }{ V }$
rho = M / V
$ \tau_g \equiv \displaystyle\frac{ m_g }{ b }$
tau_g = m_g / b
$ \tau_i \equiv \displaystyle\frac{ m_i }{ b }$
tau_i = m_i / b
$ V =\displaystyle\frac{4 \pi }{3} r ^3$
V =4* pi * r ^3/3
$ v_x = v_{0x} e^{- t / \tau }$
v_x = v_0x *exp(- t / tau )
$ v_y = g \tau + ( v_{0y} - g \tau )e^{- t / \tau }$
v_y = g * tau + ( v_0y - g * tau )*e^(- t / tau )
$ x = x_0 + v_{0x} \tau (1 - e^{- t / \tau })$
x = x_0 + v_0x * tau *(1-e^(- t / tau ))
$ y = y_0 + \tau g t + \tau ( v_{0y} - g \tau )(1 - e^{- t / \tau })$
y = y_0 + tau * g * t + tau *( v_0y - g * tau )*(1-e^(- t / tau ))
$\tau = \displaystyle\frac{2 r ^2 \rho }{9 \eta }$
tau = 2* r ^2* rho /(9 * eta )
ID:(15542, 0)
Fuerza total de cuerpo que cae en medio viscoso
Ecuación
En el caso de un cuerpo que cae en un medio viscoso, la fuerza total, la fuerza con masa constante ($F$), es igual a la fuerza gravitacional ($F_g$) menos la fuerza viscosa ($F_v$), por lo tanto,
| $ F = F_g - F_v $ |
ID:(15543, 0)
Fuerza caso masa constante
Ecuación
En el caso en que la masa inercial ($m_i$) es igual a la masa inicial ($m_0$),
| $ m_g = m_i $ |
la derivada del momento será igual a la masa multiplicada por la derivada de la velocidad ($v$). Dado que la derivada de la velocidad es la aceleración instantanea ($a$), obtenemos que la fuerza con masa constante ($F$) es igual a
| $ F = m_i a $ |
Dado que el momento ($p$) se define con la masa inercial ($m_i$) y la velocidad ($v$),
| $ p = m_i v $ |
Si la masa inercial ($m_i$) es igual a la masa inicial ($m_0$), entonces podemos derivar el momento respecto al tiempo y obtener la fuerza con masa constante ($F$):
$F=\displaystyle\frac{d}{dt}p=m_i\displaystyle\frac{d}{dt}v=m_ia$
Por lo tanto, llegamos a la conclusión de que
| $ F = m_i a $ |
ID:(10975, 0)
Fuerza gravitacional
Ecuación
La fuerza gravitacional ($F_g$) se basa en la masa gravitacional ($m_g$) del objeto y en una constante que refleja la intensidad de la gravedad en la superficie del planeta. Esta última es identificada por la aceleración gravitacional ($g$), que es igual a $9.8 m/s^2$.
En consecuencia, se concluye que:
| $ F_g = m_g g $ |
ID:(3241, 0)
Fuerza viscosa
Ecuación
La forma más simple de la fuerza viscosa ($F_v$) es aquella que es proporcional a la velocidad ($v$) del cuerpo, representada por:
| $ F_v = b v $ |
La constante de proporcionalidad, también conocida como la constante de fuerza viscosa ($b$), depende en general de la forma del objeto y de la viscosidad del medio en el que se desplaza. Un ejemplo de este tipo de fuerza es la que ejerce una corriente sobre un cuerpo esférico, cuya expresión matemática se conoce como la ley de Stokes.
ID:(3243, 0)
Fuerza de Stokes
Ecuación
La resistencia se define en función de la viscosidad del fluido y la velocidad de la esfera de la siguiente manera:
| $ F_v = b v $ |
Stokes calculó explícitamente la resistencia experimentada por la esfera y determinó que la viscosidad es proporcional al radio de la esfera y su velocidad, lo que lleva a la siguiente ecuación para la resistencia:
| $ F_v =6 \pi \eta r v $ |
ID:(4871, 0)
Factor de fuerza de Stokes
Ecuación
En el contexto de la fuerza de Stokes en la fuerza viscosa ($F_v$), esta se modela con la constante de fuerza viscosa ($b$) y la velocidad ($v$), como se muestra en la ecuación:
| $ F_v = b v $ |
Esto se traduce en un valor específico de la constante de fuerza viscosa ($b$), que, junto con la viscosidad ($\eta$) y el radio de la gota ($r$), puede expresarse como:
| $ b \equiv 6 \pi \eta r $ |
ID:(15554, 0)
Ecuación de movimiento caida en medio viscoso
Ecuación
La fuerza con masa constante ($F$) es igual a la fuerza gravitacional ($F_g$) menos la fuerza viscosa ($F_v$) por lo que:
| $ F = F_g - F_v $ |
Esta relación permite establecer la ecuación de movimiento para la aceleración instantanea ($a$) con una masa inercial ($m_i$) que cae debido a la gravedad terrestre con la aceleración gravitacional ($g$), y con una masa gravitacional ($m_g$), en la constante de fuerza viscosa ($b$), tomará la forma de:
| $ m_i a = m_g g - b v $ |
ID:(14495, 0)
Masa y Densidad
Ecuación
La densidad ($\rho$) se define como la relación entre la masa ($M$) y el volumen ($V$), que se expresa como:
| $ \rho \equiv\displaystyle\frac{ m_i }{ V }$ |
| $ \rho \equiv\displaystyle\frac{ M }{ V }$ |
Esta propiedad es específica del material en cuestión.
ID:(3704, 0)
Volumen de esfera
Ecuación
La volumen de una esfera ($V$) para una esfera con un radio de una esfera ($r$) se calcula mediante la siguiente fórmula:
| $ V =\displaystyle\frac{4 \pi }{3} r ^3$ |
ID:(4445, 0)
Igualdad de masa inercial y gravitacional
Ecuación
Las masas que Newton utilizó en sus principios están relacionadas con la inercia de los cuerpos, lo que lleva al concepto de la masa inercial ($m_i$).
La ley de Newton que se vincula con la fuerza entre cuerpos debido a sus masas está relacionada con la gravedad, por lo que se conoce como la masa gravitacional ($m_g$).
De manera empírica, se ha concluido que ambas masas son equivalentes, y por lo tanto, definimos
| $ m_g = m_i $ |
Einstein fue quien cuestionó esta igualdad y, a partir de esa duda, comprendió por qué ambas 'aparecen' iguales en su teoría de la gravedad. En su argumento, Einstein explicó que las masas deforman el espacio, y esta deformación del espacio provoca un cambio en el comportamiento de los cuerpos. De esta manera, las masas resultan ser equivalentes. El concepto revolucionario de la curvatura del espacio implica que incluso la luz, que carece de masa, se ve afectada por los cuerpos celestes, lo que contradice la teoría de la gravitación de Newton. Esto se demostró experimentalmente al estudiar el comportamiento de la luz durante un eclipse solar. En esta situación, los haces de luz se desvían debido a la presencia del sol, lo que permite observar estrellas que se encuentran detrás de él.
ID:(12552, 0)
Tiempo característico de la ecuación de Stokes
Ecuación
Con el modelo de Stokes, la resistencia viscosa la constante de fuerza viscosa ($b$), que depende de el radio de la gota ($r$) y la viscosidad del medio ($\eta$), se calcula como:
| $ b \equiv 6 \pi \eta r $ |
Esto conduce a que la tiempo de viscosidad y masa inercial ($\tau_i$) y la tiempo de viscosidad y masa gravitacional ($\tau_g$) asuman valores iguales la tiempo de adaptación ($\tau$), que se calculan con la densidad ($\rho$) de la siguiente manera:
| $\tau = \displaystyle\frac{2 r ^2 \rho }{9 \eta }$ |
Si el tiempo característico se define como
$\tau=\displaystyle\frac{m_i}{b}$
y el coeficiente de la fuerza viscosa es
$b=6\pi r\eta$
Por otro lado, dado que
| $ \rho \equiv\displaystyle\frac{ m_i }{ V }$ |
y
| $ V =\displaystyle\frac{4 \pi }{3} r ^3$ |
se tiene que la masa es
$m_i = \rho V = \displaystyle\frac{4\pi}{3} r^3 \rho$
lo que nos lleva a
$\tau = \displaystyle\frac{m_i}{b}=\displaystyle\frac{2 \rho r^2}{9\eta}$
en otras palabras,
| $\tau = \displaystyle\frac{2 r ^2 \rho }{9 \eta }$ |
ID:(14465, 0)
Tiempo de masa gravitacional y viscosidad
Ecuación
Con la ecuación de movimiento de un cuerpo en un medio viscoso, tenemos la derivada de la velocidad ($v$) en el tiempo ($t$) con la masa inercial ($m_i$), la masa gravitacional ($m_g$), la constante de fuerza viscosa ($b$) y la aceleración gravitacional ($g$):
| $ m_i \displaystyle\frac{dv}{dt} = m_g g - b v $ |
Lo que define la tiempo de viscosidad y masa gravitacional ($\tau_g$) como:
| $ \tau_g \equiv \displaystyle\frac{ m_g }{ b }$ |
ID:(15549, 0)
Velocidad horizontal en medio viscoso
Ecuación
En un escenario de movimiento horizontal, la esfera enfrenta una resistencia que proviene únicamente de la viscosidad del medio circundante, la cual puede ser cuantificada mediante la ecuación de la velocidad ($v$) con la velocidad inicial ($v_0$), la tiempo de viscosidad y masa inercial ($\tau_i$) y el tiempo ($t$):
| $ v = v_0 e^{- t / \tau_i }$ |
Por lo tanto, la interacción entre estos elementos conduce a la observación de que la componente x de la velocidad ($v_x$) con la velocidad horizontal inicial ($v_{0x}$), la tiempo de adaptación ($\tau$) y el tiempo ($t$):
| $ v_x = v_{0x} e^{- t / \tau }$ |
ID:(6844, 0)
Posición horizontal medio viscoso
Ecuación
En el contexto del movimiento horizontal, la posición se obtiene mediante la integración de la velocidad, lo que nos da como resultado una ecuación en la posición ($s$) con la posición inicial ($s_0$), la velocidad inicial ($v_0$), la tiempo de viscosidad y masa gravitacional ($\tau_g$), la tiempo de viscosidad y masa inercial ($\tau_i$), la aceleración gravitacional ($g$) y el tiempo ($t$):
| $ s = s_0 + v_0 \tau_i (1 - e^{- t / \tau_i })$ |
A partir de esta ecuación, llegamos a la ecuación el desplazameinto horizontal para la posición en el eje x ($x$) con la posición inicial en el eje x ($x_0$), la velocidad horizontal inicial ($v_{0x}$), la tiempo de adaptación ($\tau$) y el tiempo ($t$):
| $ x = x_0 + v_{0x} \tau (1 - e^{- t / \tau })$ |
ID:(14467, 0)
Tiempo de masa inercial y viscosidad
Ecuación
Con la ecuación de movimiento de un cuerpo en un medio viscoso, tenemos la derivada de la velocidad ($v$) en el tiempo ($t$) con la constante de fuerza viscosa ($b$) y la aceleración gravitacional ($g$):
| $ m_i \displaystyle\frac{dv}{dt} = - b v $ |
Lo que define la tiempo de viscosidad y masa inercial ($\tau_i$) como:
| $ \tau_i \equiv \displaystyle\frac{ m_i }{ b }$ |
ID:(15548, 0)
Velocidad vertical en medio viscoso bajo la gravedad
Ecuación
En el contexto del movimiento vertical, la esfera enfrenta una doble resistencia: por un lado, la viscosidad del medio circundante, y por otro, la gravedad que la impulsa hacia abajo. Esta última puede ser cuantificada mediante la ecuación de la velocidad ($v$) con la velocidad inicial ($v_0$), la tiempo de viscosidad y masa gravitacional ($\tau_g$), la tiempo de viscosidad y masa inercial ($\tau_i$), la aceleración gravitacional ($g$) y el tiempo ($t$):
| $ v = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
Assumimos que la masa gravitacional y la masa inercial son idénticas, entonces obtenemos la función para la componente y de la velocidad ($v_y$) con la velocidad vertical inicial ($v_{0y}$), la tiempo de adaptación ($\tau$), la aceleración gravitacional ($g$) y el tiempo ($t$):
| $ v_y = g \tau + ( v_{0y} - g \tau )e^{- t / \tau }$ |
ID:(14466, 0)
Posición vertical medio viscoso bajo gravitación
Ecuación
En el escenario de movimiento vertical, la posición se obtiene mediante la integración de la velocidad, lo que nos da como resultado una ecuación en la posición ($s$) con la posición inicial ($s_0$), la velocidad inicial ($v_0$), la tiempo de viscosidad y masa gravitacional ($\tau_g$), la tiempo de viscosidad y masa inercial ($\tau_i$), la aceleración gravitacional ($g$) y el tiempo ($t$):
| $ s = s_0 + g \tau_g t +( v_0 - g \tau_g ) \tau_i (1 - e^{- t / \tau_i })$ |
A partir de esta ecuación, llegamos a la ecuación para el desplazamiento vertical de la posición en el eje y ($y$) con la posición inicial en el eje y ($y_0$), la velocidad horizontal inicial ($v_{0x}$), la tiempo de adaptación ($\tau$) y el tiempo ($t$):
| $ y = y_0 + \tau g t + \tau ( v_{0y} - g \tau )(1 - e^{- t / \tau })$ |
ID:(14468, 0)