Utilizador:
Fluxo laminar, tinta
Descrição
Uma forma eficaz de mostrar o fluxo laminar é injetar tinta em um fluxo usando uma agulha fina que não o perturbe. Essa técnica permite a visualização clara das camadas de fluido deslizando sem se misturar entre si. A tinta se dispersa no fluido de maneira ordenada, criando linhas distintas que revelam a direção e o padrão do fluxo laminar. Esse método é amplamente utilizado em experimentos e demonstrações para ilustrar visualmente as características e propriedades do fluxo laminar de maneira impactante.
ID:(7059, 0)
Imagens de fluxo laminar
Descrição
A observação em laboratório mostra como a tinta desenha uma linha (neste caso, vermelha). Se o experimento for repetido em diferentes posições, é observado um padrão de camadas, indicando que o fluxo é laminar.
Líquidos que fluem de forma laminar apresentam um canal suave, sem a formação de redemoinhos ou movimentos laterais bruscos.
ID:(7060, 0)
Escoamento laminar em torno de uma esfera
Descrição
Um exemplo de fluxo laminar ao redor de uma esfera demonstra que as camadas de fluido se movem mantendo sua paralelismo.
Aqui está uma imagem que ilustra o cálculo do fluxo entre duas placas e uma esfera/cilindro (link para a imagem: http://luxsignifer.blogspot.com/2016/10/hele-shaw-flow-past-circle.html).
Essa situação ocorre quando o número de Reynolds $Re$ é menor que 5.
ID:(1889, 0)
Fluxo de mel
Descrição
Existem líquidos que exibem um comportamento peculiar, pois parecem fluir em câmera lenta. Um exemplo clássico desse fenômeno é o mel.
A causa subjacente desse comportamento é a força viscosa que é gerada quando uma camada de líquido desliza ou se move em relação às suas camadas adjacentes. Essa força viscosa é proporcional à variação de velocidade entre as camadas do líquido dividida pela espessura da camada em consideração.
ID:(1655, 0)
Folhas no córrego
Conceito
No fluxo laminar, camadas adjacentes se movem e existe uma força gerada pela viscosidade entre elas. A camada mais rápida arrasta sua vizinha mais lenta, enquanto a mais lenta restringe o avanço da mais rápida.
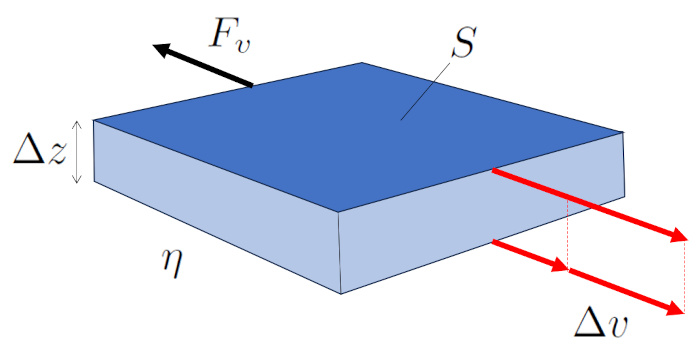
Portanto, a força la força viscosa ($F_v$) gerada por ($$) sobre a outra é uma função de ($$), ($$) e ($$), como mostrado na seguinte equação:
| $ F_v =- S \eta \displaystyle\frac{ \Delta v }{ \Delta z }$ |
ilustrado no seguinte diagrama:
ID:(7053, 0)
Força viscosa
Equação
Quando um líquido de viscosidade $\eta$ flui entre duas superfícies $S$ a uma distância $dz$ com uma diferença de velocidade $dv_x$, ele experimenta uma força de viscosidade $F_v$ dada pela lei de Newton da viscosidade:
 $ F_v =- S \eta \displaystyle\frac{ \Delta v }{ \Delta z }$ |
ID:(3622, 0)
Fluir através de um cilindro
Conceito
O fluxo laminar ao redor de um cilindro pode ser representado como múltiplas camadas cilíndricas deslizando sob a influência das camadas adjacentes. Nesse caso, la força viscosa ($F_v$) com o comprimento do tubo ($\Delta L$), la viscosidade ($\eta$) e as variáveis la posição radial no cilindro ($r$) e la velocidade em um raio do cilindro ($v$) é expresso como:
| $ F_v =-2 \pi r \Delta L \eta \displaystyle\frac{ dv }{ dr }$ |
A camada na borda em ($$) permanece estacionária devido ao efeito de borda e, através de la viscosidade ($\eta$), retarda a camada adjacente que possui velocidade.
O centro é a parte que se move em la taxa de fluxo máxima ($v_{max}$), arrastando a camada circundante. Por sua vez, essa camada arrasta a próxima e assim por diante até atingir a camada em contato com a parede do cilindro, que está estacionária.
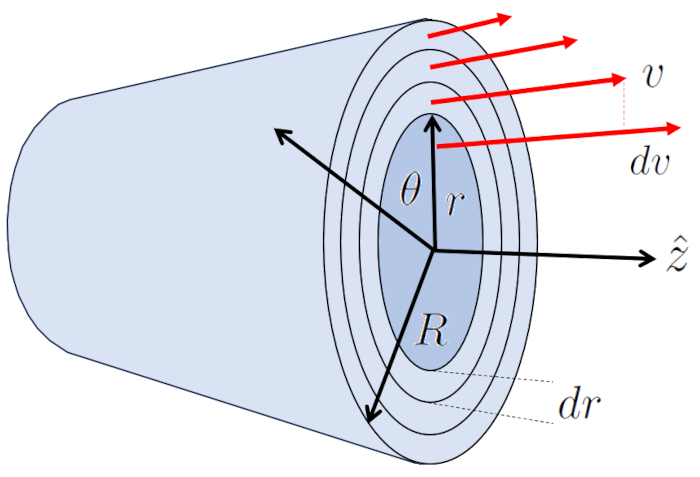
Dessa forma, o sistema transfere energia do centro para a parede, gerando um perfil de velocidade representado por:
| $ v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$ |
com:
| $ v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
ID:(7057, 0)
Força viscosa, caixa do cilindro
Equação
Uma força viscosa ($F_v$) gerada por um líquido com viscosidade ($\eta$) entre algumas superfícies paralelas ($S$) e uma distância entre superfícies ($\Delta z$), juntamente com uma diferença de velocidade entre superfícies ($\Delta v$) e la velocidade em um raio do cilindro ($v$), é calculada da seguinte forma:
| $ F_v =- S \eta \displaystyle\frac{ \Delta v }{ \Delta z }$ |
No caso de um cilindro, a superfície é definida por comprimento do tubo ($\Delta L$) e pelo perímetro de cada um dos cilindros internos, que é calculado multiplicando $2\pi$ por o raio de posição em um tubo ($r$). Com isso, la força de resistência no cilindro ($F_v$) é calculada usando la viscosidade ($\eta$) e la variação de velocidade entre dois raios ($dv$) para a largura do cilindro o variação do raio em um tubo ($dr$), resultando em:
| $ F_v =-2 \pi r \Delta L \eta \displaystyle\frac{ dv }{ dr }$ |
Como a força viscosa é
| $ F_v =- S \eta \displaystyle\frac{ \Delta v }{ \Delta z }$ |
e a superfície do cilindro é
$S=2\pi R L$
onde $R$ é o raio e $L$ é o comprimento do canal, a força viscosa pode ser expressa como
| $ F_v =-2 \pi r \Delta L \eta \displaystyle\frac{ dv }{ dr }$ |
onde $\eta$ representa a viscosidade e $dv/dr$ é o gradiente de velocidade entre a parede e o fluxo.
ID:(3623, 0)
0
Video
Vídeo: Fluxo Laminar