Benützer:
Laminare Strömung
Storyboard
Wenn die Reynold-Zahl sehr klein ist, ist die Strömung laminar. Dies zeigt, dass die Strömung als eine Reihe von Blättern ohne das Auftreten von Strudeln dargestellt werden kann und dass sie sich an die Randbedingungen anpasst und harmonisch fließt.
ID:(879, 0)
Laminar Flow, Tinte
Beschreibung
Eine effektive Methode, um laminare Strömung zu zeigen, besteht darin, Tinte in einen Fluss einzuspritzen, indem eine dünne Nadel verwendet wird, die diesen nicht stört. Diese Technik ermöglicht eine klare Visualisierung der Flüssigkeitsschichten, die sich ohne Vermischung gegeneinander bewegen. Die Tinte verteilt sich geordnet im Fluid und erzeugt deutlich erkennbare Linien, die die Richtung und das Muster der laminaren Strömung offenbaren. Diese Methode wird häufig in Experimenten und Demonstrationen eingesetzt, um die Merkmale und Eigenschaften der laminaren Strömung auf visuell beeindruckende Weise zu veranschaulichen.
ID:(7059, 0)
Laminare Strömungsbilder
Beschreibung
Die Beobachtung im Labor zeigt, wie Tinte eine Linie zieht (in diesem Fall rot). Wenn das Experiment an verschiedenen Positionen wiederholt wird, zeigt sich ein Schichtmuster, was auf laminare Strömung hinweist.
Flüssigkeiten, die laminar fließen, zeigen einen sanften Kanal, ohne Wirbelbildung oder abrupte seitliche Bewegungen.
ID:(7060, 0)
Laminare Strömung um eine Kugel
Beschreibung
Ein Beispiel für laminare Strömung um eine Kugel zeigt, dass die Flüssigkeitsschichten sich parallel zueinander bewegen.
Hier ist ein Bild, das die Berechnung des Flusses zwischen zwei Platten und einer Kugel/Zylinder darstellt (Link zum Bild: http://luxsignifer.blogspot.com/2016/10/hele-shaw-flow-past-circle.html).
Diese Situation tritt auf, wenn die Reynolds-Zahl $Re$ kleiner als 5 ist.
ID:(1889, 0)
Honig Fluss
Beschreibung
Es gibt Flüssigkeiten, die ein eigenartiges Verhalten zeigen, da sie scheinbar in Zeitlupe fließen. Ein klassisches Beispiel für dieses Phänomen ist Honig.
Die zugrunde liegende Ursache dieses Verhaltens ist die viskose Kraft, die entsteht, wenn sich eine Schicht Flüssigkeit relativ zu ihren benachbarten Schichten verschiebt oder bewegt. Diese viskose Kraft ist proportional zur Geschwindigkeitsänderung zwischen den Flüssigkeitsschichten geteilt durch die Dicke der betrachteten Schicht.
ID:(1655, 0)
Laminare im Strom
Konzept
Im laminaren Fluss bewegen sich benachbarte Schichten, und zwischen ihnen wirkt eine durch die Viskosität erzeugte Kraft. Die schnellere Schicht zieht ihre langsamere Nachbarschicht mit, während die langsamere Schicht den Fortschritt der schnelleren einschränkt.
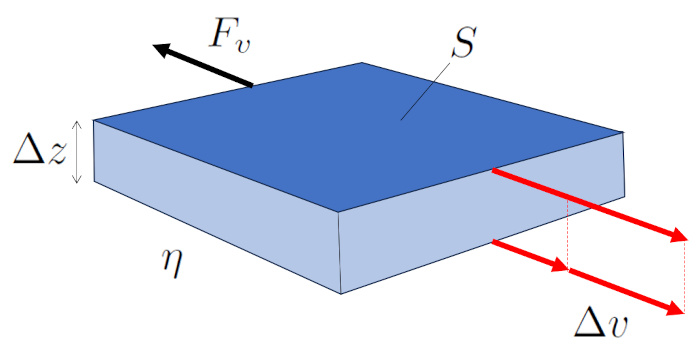
Daher ist die Kraft die Viscose Kraft ($F_v$), die von ($$) über die andere erzeugt wird, eine Funktion von ($$), ($$) und ($$), wie in der folgenden Gleichung dargestellt:
| $ F_v =- S \eta \displaystyle\frac{ \Delta v }{ \Delta z }$ |
illustriert im folgenden Diagramm:
ID:(7053, 0)
Viscose Kraft
Gleichung
Wenn eine Flüssigkeit mit Viskosität $\eta$ zwischen zwei Oberflächen $S$ mit einem Abstand $dz$ und einer Geschwindigkeitsdifferenz $dv_x$ fließt, erfährt sie eine viskose Kraft $F_v$, die durch das Gesetz von Newton für die Viskosität gegeben ist:
 $ F_v =- S \eta \displaystyle\frac{ \Delta v }{ \Delta z }$ |
ID:(3622, 0)
Durch einen Zylinder fließen
Konzept
Der laminare Fluss um einen Zylinder kann als mehrere zylindrische Schichten dargestellt werden, die unter dem Einfluss benachbarter Schichten gleiten. In diesem Fall wird die Viscose Kraft ($F_v$) mit der Rohrlänge ($\Delta L$), die Viskosität ($\eta$) und den Variablen die Zylinder-Stern Position ($r$) und die Geschwindigkeit auf einer Zylinder-Radio ($v$) wie folgt ausgedrückt:
| $ F_v =-2 \pi r \Delta L \eta \displaystyle\frac{ dv }{ dr }$ |
Die Schicht am Rand bei ($$) bleibt aufgrund des Randeffekts stehen und verlangsamt durch die Viskosität ($\eta$) die benachbarte Schicht, die eine Geschwindigkeit hat.
Das Zentrum ist der Teil, der sich mit die Maximale Durchflussrate ($v_{max}$) bewegt und die umgebende Schicht mitzieht. Diese Schicht zieht wiederum die nächste Schicht und so weiter, bis sie die Schicht erreicht, die Kontakt mit der Zylinderwand hat, die sich nicht bewegt.
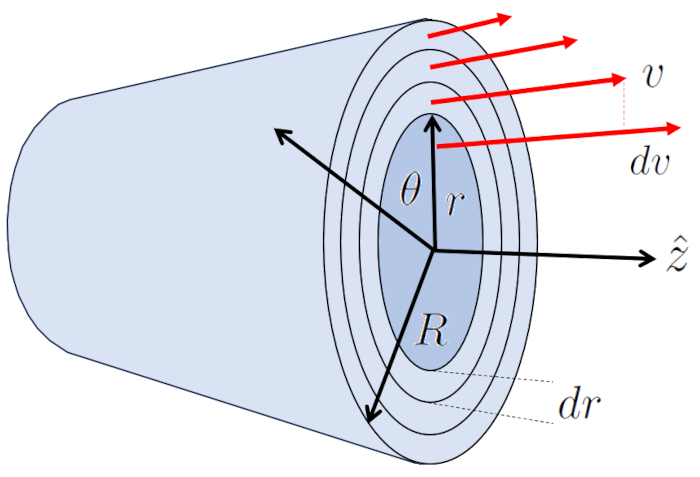
Auf diese Weise überträgt das System Energie von der Mitte zur Wand und erzeugt ein Geschwindigkeitsprofil, das wie folgt dargestellt wird:
| $ v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$ |
mit:
| $ v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
ID:(7057, 0)
Viscose Kraft, zylindrischer Fall
Gleichung
Eine Viscose Kraft ($F_v$), die von einer Flüssigkeit mit Viskosität ($\eta$) zwischen manche Parallele Flächen ($S$) und eine Abstand zwischen Oberflächen ($\Delta z$) erzeugt wird, zusammen mit eine Geschwindigkeitsunterschied zwischen Oberflächen ($\Delta v$) und die Geschwindigkeit auf einer Zylinder-Radio ($v$), wird wie folgt berechnet:
| $ F_v =- S \eta \displaystyle\frac{ \Delta v }{ \Delta z }$ |
Im Falle eines Zylinders wird die Oberfläche durch Rohrlänge ($\Delta L$) definiert und durch den Umfang jeder der internen Zylinder, der durch die Multiplikation von $2\pi$ mit der Positionsradius in einem Rohr ($r$) berechnet wird. Damit wird die Zylinderwiderstandskraft ($F_v$) unter Verwendung von die Viskosität ($\eta$) und die Geschwindigkeitsvariation zwischen zwei Radien ($dv$) für die Breite des Zylinders der Radiusvariation in einem Rohr ($dr$) berechnet, was zu folgendem Ergebnis führt:
| $ F_v =-2 \pi r \Delta L \eta \displaystyle\frac{ dv }{ dr }$ |
Da die viskose Kraft gegeben ist als
| $ F_v =- S \eta \displaystyle\frac{ \Delta v }{ \Delta z }$ |
und die Oberfläche des Zylinders ist
$S=2\pi R L$
wobei $R$ der Radius und $L$ die Länge des Kanals ist, kann die viskose Kraft ausgedrückt werden als
| $ F_v =-2 \pi r \Delta L \eta \displaystyle\frac{ dv }{ dr }$ |
wobei $\eta$ die Viskosität repräsentiert und $dv/dr$ den Geschwindigkeitsgradienten zwischen der Wand und dem Fluss darstellt.
ID:(3623, 0)
0
Video
Video: Laminare Strmung