Flux laminaire, encre
Définition 
Une manière efficace de montrer l'écoulement laminaire est d'injecter de l'encre dans un flux à l'aide d'une aiguille fine qui ne le perturbe pas. Cette technique permet de visualiser clairement les couches de fluide glissant les unes sur les autres sans se mélanger. L'encre se dispersera dans le fluide de manière ordonnée, créant des lignes distinctes qui révèlent la direction et le motif de l'écoulement laminaire. Cette méthode est largement utilisée dans les expériences et les démonstrations pour illustrer de manière visuellement impactante les caractéristiques et les propriétés de l'écoulement laminaire.

ID:(7059, 0)
Images de flux laminaire
Image 
L'observation en laboratoire montre comment l'encre dessine une ligne (dans ce cas, rouge). Si l'expérience est répétée à différentes positions, on observe un schéma de couches, ce qui indique un écoulement laminaire.

Les liquides s'écoulant de manière laminaire présentent un écoulement régulier, sans tourbillons ni mouvements latéraux brusques.
ID:(7060, 0)
Ecoulement laminaire autour d'une sphère
Noter 
Un exemple d'écoulement laminaire autour d'une sphère montre que les couches de fluide se déplacent tout en maintenant leur parallélisme.

Voici une image illustrant le calcul du flux entre deux plaques et une sphère/cylindre (lien vers l'image : http://luxsignifer.blogspot.com/2016/10/hele-shaw-flow-past-circle.html).
Cette situation se produit lorsque le nombre de Reynolds (Re) est inférieur à 5.
ID:(1889, 0)
Coulée de miel
Citation 
Il existe des liquides qui présentent un comportement particulier, car ils semblent s'écouler au ralenti. Un exemple classique de ce phénomène est le miel.

La cause sous-jacente de ce comportement est la force visqueuse qui se produit lorsqu'une couche de liquide glisse ou se déplace par rapport à ses couches adjacentes. Cette force visqueuse est proportionnelle à la variation de vitesse entre les couches du liquide divisée par l'épaisseur de la couche en question.
ID:(1655, 0)
Foils dans le courant
Exercer 
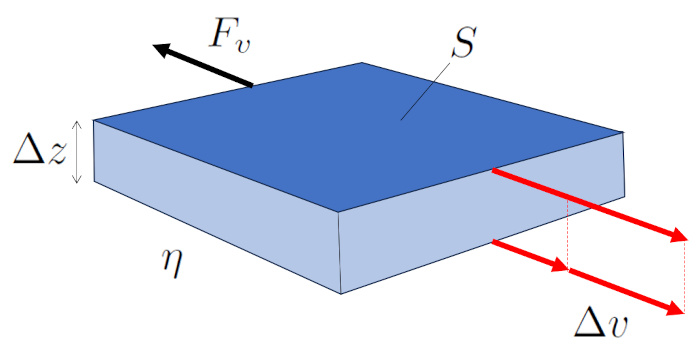
Dans un écoulement laminaire, des couches adjacentes se déplacent et une force est générée par la viscosité entre elles. La couche la plus rapide entraîne sa voisine plus lente, tandis que la plus lente limite l'avancement de la plus rapide.
Par conséquent, la force a force visqueuse ($F_v$) générée par ERROR:10119.1 sur l'autre est une fonction de ERROR:5556.1, ERROR:5436.1 et ERROR:5422.1, comme indiqué dans l'équation suivante :
| $ F_v =- S \eta \displaystyle\frac{ \Delta v }{ \Delta z }$ |
illustrée dans le schéma suivant :
ID:(7053, 0)
S'écouler dans un cylindre
Équation 
L'écoulement laminaire autour d'un cylindre peut être représenté comme plusieurs couches cylindriques glissant sous l'influence des couches adjacentes. Dans ce cas, a force visqueuse ($F_v$) avec le longueur du tube ($\Delta L$), a viscosité ($\eta$) et les variables a position radiale dans le cylindre ($r$) et a vitesse dans un rayon du cylindre ($v$) est exprimée comme suit :
La couche à la frontière à ERROR:5417.1 reste stationnaire en raison de l'effet de bord et, à travers a viscosité ($\eta$), ralentit la couche adjacente qui a une vitesse.
Le centre est la partie qui se déplace à A vitesse maximal ($v_{max}$), entraînant la couche environnante. À son tour, cette couche entraîne la suivante, et ainsi de suite jusqu'à ce qu'elle atteigne la couche en contact avec la paroi du cylindre, qui est immobile.
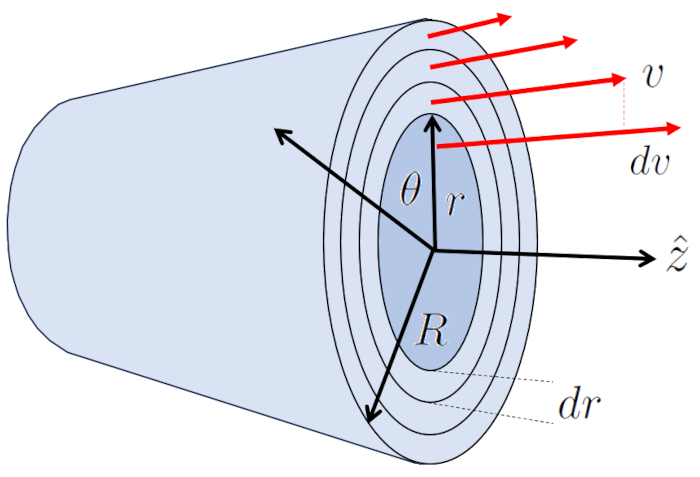
Ainsi, le système transfère de l'énergie du centre vers la paroi, générant un profil de vitesse représenté par :
avec :
ID:(7057, 0)
Flux laminaire
Storyboard 
Variables
Calculs
Calculs
Équations
En fran ais, l' nonc donn serait le suivant :
"Comme la force visqueuse est
et la surface du cylindre est
$S=2\pi R L$
o $R$ est le rayon et $L$ est la longueur du canal, la force visqueuse peut tre exprim e comme
o $\eta$ repr sente la viscosit et $dv/dr$ est le gradient de vitesse entre la paroi et l' coulement.
Exemples
Une mani re efficace de montrer l' coulement laminaire est d'injecter de l'encre dans un flux l'aide d'une aiguille fine qui ne le perturbe pas. Cette technique permet de visualiser clairement les couches de fluide glissant les unes sur les autres sans se m langer. L'encre se dispersera dans le fluide de mani re ordonn e, cr ant des lignes distinctes qui r v lent la direction et le motif de l' coulement laminaire. Cette m thode est largement utilis e dans les exp riences et les d monstrations pour illustrer de mani re visuellement impactante les caract ristiques et les propri t s de l' coulement laminaire.
L'observation en laboratoire montre comment l'encre dessine une ligne (dans ce cas, rouge). Si l'exp rience est r p t e diff rentes positions, on observe un sch ma de couches, ce qui indique un coulement laminaire.
Les liquides s' coulant de mani re laminaire pr sentent un coulement r gulier, sans tourbillons ni mouvements lat raux brusques.
Un exemple d' coulement laminaire autour d'une sph re montre que les couches de fluide se d placent tout en maintenant leur parall lisme.
Cette situation se produit lorsque le nombre de Reynolds (Re) est inf rieur 5.
Il existe des liquides qui pr sentent un comportement particulier, car ils semblent s' couler au ralenti. Un exemple classique de ce ph nom ne est le miel.
La cause sous-jacente de ce comportement est la force visqueuse qui se produit lorsqu'une couche de liquide glisse ou se d place par rapport ses couches adjacentes. Cette force visqueuse est proportionnelle la variation de vitesse entre les couches du liquide divis e par l' paisseur de la couche en question.
Dans un coulement laminaire, des couches adjacentes se d placent et une force est g n r e par la viscosit entre elles. La couche la plus rapide entra ne sa voisine plus lente, tandis que la plus lente limite l'avancement de la plus rapide.
Par cons quent, la force a force visqueuse ($F_v$) g n r e par ERROR:10119.1 sur l'autre est une fonction de ERROR:5556.1, ERROR:5436.1 et ERROR:5422.1, comme indiqu dans l' quation suivante :
illustr e dans le sch ma suivant :
A force visqueuse ($F_v$) peut tre calcul partir de les surfaces parallèles ($S$), a viscosité ($\eta$), a différence de vitesse entre les surfaces ($\Delta v$) et a distance entre les surfaces ($\Delta z$) en utilisant la m thode suivante :
L' coulement laminaire autour d'un cylindre peut tre repr sent comme plusieurs couches cylindriques glissant sous l'influence des couches adjacentes. Dans ce cas, a force visqueuse ($F_v$) avec le longueur du tube ($\Delta L$), a viscosité ($\eta$) et les variables a position radiale dans le cylindre ($r$) et a vitesse dans un rayon du cylindre ($v$) est exprim e comme suit :
La couche la fronti re ERROR:5417.1 reste stationnaire en raison de l'effet de bord et, travers a viscosité ($\eta$), ralentit la couche adjacente qui a une vitesse.
Le centre est la partie qui se d place a vitesse maximal ($v_{max}$), entra nant la couche environnante. son tour, cette couche entra ne la suivante, et ainsi de suite jusqu' ce qu'elle atteigne la couche en contact avec la paroi du cylindre, qui est immobile.
Ainsi, le syst me transf re de l' nergie du centre vers la paroi, g n rant un profil de vitesse repr sent par :
avec :
Dans le cas d'un cylindre, la surface est d finie par ERROR:5430,0, et par le p rim tre de chacun des cylindres internes, qui est calcul en multipliant $2\pi$ par le rayon de position dans un tube ($r$). Avec cela, a force de résistance en cylindre ($F_v$) est calcul e en utilisant a viscosité ($\eta$) et a variation de vitesse entre deux rayons ($dv$) pour la largeur du cylindre le variation de rayon dans un tube ($dr$), ce qui donne :
ID:(879, 0)
